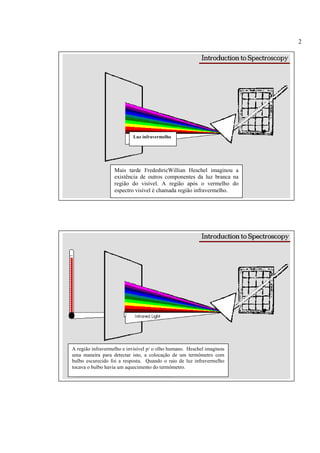
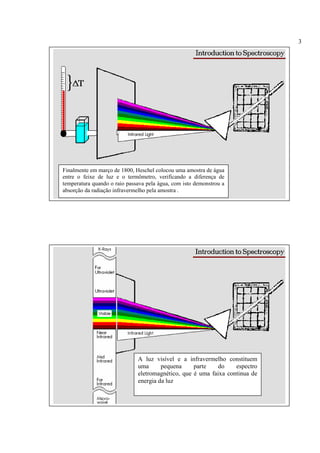
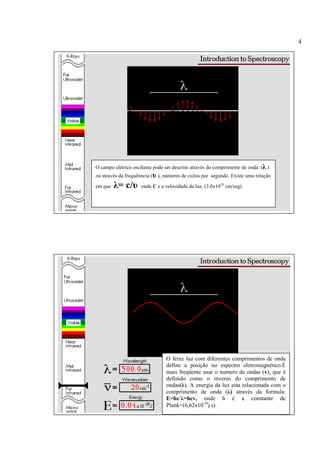
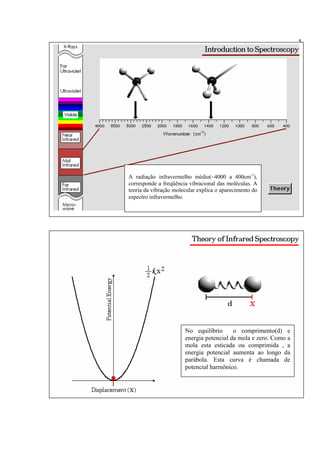
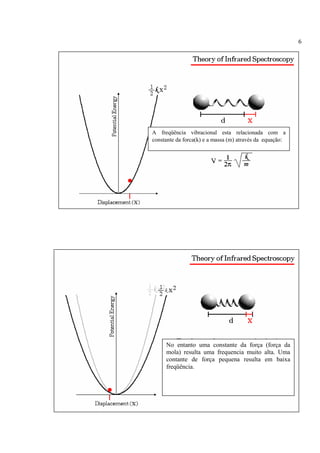
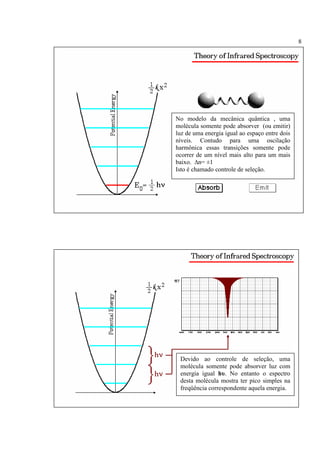
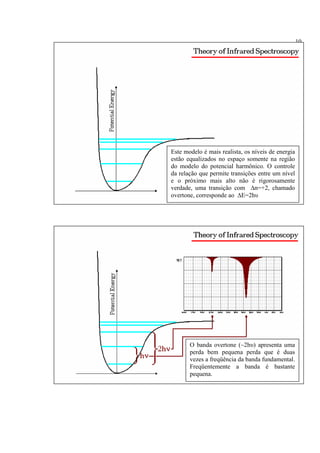
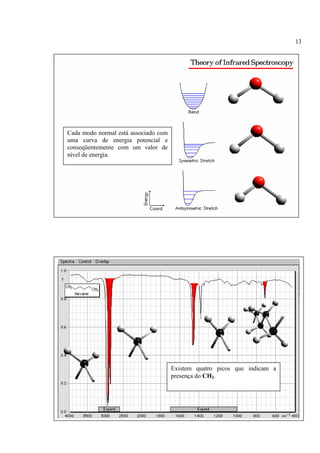
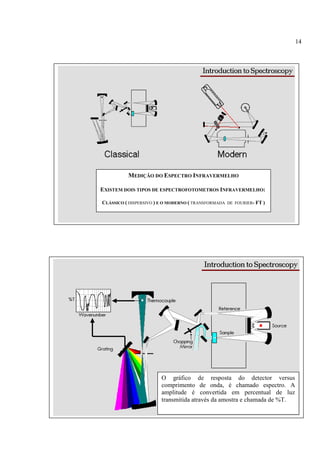
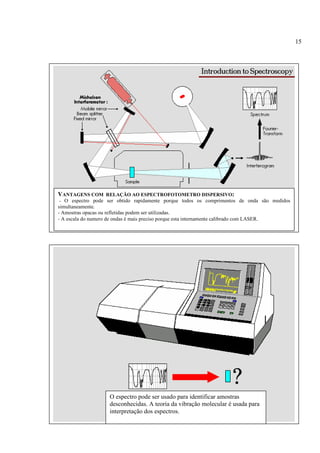
A espectroscopia infravermelho mede a absorção de radiação eletromagnética por moléculas. Moléculas absorvem energia quantizada igual a hυ durante transições vibracionais e de rotação. O espectro infravermelho fornece informações sobre os modos normais de vibração e identidade química de uma amostra.

1. 1
Introdução a Espectroscopia
O que é a espectroscopia infravermelho?
A estória da espectroscopia infravermelho começa
com Isac Newton. Ele imaginou um experimento
quando um raio de luz passava através da fresca de
uma janela.
Newton mostrou que a luz branca era
decomposta em diferentes cores ao
passar por um prisma.

2. 2
Luz infravermelho
Mais tarde FredediricWillian Heschel imaginou a
existência de outros componentes da luz branca na
região do visível. A região após o vermelho do
espectro visível é chamada região infravermelho.
A região infravermelho e invisível p/ o olho humano. Heschel imaginou
uma maneira para detectar isto, a colocação de um termômetro com
bulbo escurecido foi a resposta. Quando o raio de luz infravermelho
tocava o bulbo havia um aquecimento do termômetro.

3. 3
Finalmente em março de 1800, Heschel colocou uma amostra de água
entre o feixe de luz e o termômetro, verificando a diferença de
temperatura quando o raio passava pela água, com isto demonstrou a
absorção da radiação infravermelho pela amostra .
A luz visível e a infravermelho constituem
uma pequena parte do espectro
eletromagnético, que é uma faixa continua de
energia da luz

4. 4
O campo elétrico oscilante pode ser descrito através do comprimento de onda (λ )
ou através da frequênncia (υ ), números de ciclos por segundo. Existe uma relação
em que λ= c/υ onde C e a velocidade da luz. (3.0x1010 cm/seg).
O feixe luz com diferentes comprimentos de onda
define a posição no espectro eletromagnético.É
mais freqüente usar o numero de ondas (v), que é
definido como o inverso do comprimento de
ondas(λ). A energia da luz esta relacionada com o
comprimento de onda (λ) através da formula:
E=hc/λ=hcv, onde h é a constante de
Plank=(6,62x10-34j.s)

5. 5
A radiação infravermelho médio(~4000 a 400cm-1),
corresponde a freqüência vibracional das moléculas. A
teoria da vibração molecular explica o aparecimento do
espectro infravermelho.
No equilíbrio o comprimento(d) e
energia potencial da mola e zero. Como a
mola esta esticada ou comprimida , a
energia potencial aumenta ao longo da
parábola. Esta curva é chamada de
potencial harmônico.

6. 6
A freqüência vibracional esta relacionada com a
constante da forca(k) e a massa (m) através da equação:
No entanto uma constante da força (força da
mola) resulta uma frequencia muito alta. Uma
contante de força pequena resulta em baixa
freqüência.

7. 7
Quando a mola é esticada a um valor arbitrário
e depois retorna, esta vibração tem energia
total igual a E=1/2kx2(maximo). O modelo prediz
que uma molécula pode vibra até um valor
máximo o que é correto para a bola mais não é
correto para a molécula.
MODELO DA MOLECULA P/ A MECÂNICA QUÂNTICA.
A mecânica quântica prediz relações iguais entre
pequenas vibrações. A constante da força (K) e da
massa é predita pela física clássica. Contudo a
mecânica quântica prediz que a molécula pode
normalmente vibrar a um nível de energia
conforme a formula:
E = (n+1/2)hυ n=0,1,2,3....
A constante de Plank’s = (6,62x10-34joule.s)
A energia liberada pode ser QUANTIZADA.

8. 8
No modelo da mecânica quântica , uma
molécula somente pode absorver (ou emitir)
luz de uma energia igual ao espaço entre dois
níveis. Contudo para uma oscilação
harmônica essas transições somente pode
ocorrer de um nível mais alto para um mais
baixo. ∆n= ±1
Isto é chamado controle de seleção.
Devido ao controle de seleção, uma
molécula somente pode absorver luz com
energia igual hυ. No entanto o espectro
desta molécula mostra ter pico simples na
freqüência correspondente aquela energia.

9. 9
A freqüência mais alta resulta de um
espaço maior entre os níveis de energia, e
as freqüências mais baixas resultam dos
espaços menores entre os respectivos
níveis.
Este espectro é mais complicado que o mostrado
acima, porque uma molécula real não é um
oscilador harmônico. Quando átomos são
empurrados em conjunto, eles se repelem muito
mais que uma mola. Este comportamento pode ser
modelado com potencial não harmônico.

10. 10
Este modelo é mais realista, os níveis de energia
estão equalizados no espaço somente na região
do modelo do potencial harmônico. O controle
da relação que permite transições entre um nível
e o próximo mais alto não é rigorosamente
verdade, uma transição com ∆n=+2, chamado
overtone, corresponde ao ∆E=2hυ
O banda overtone (~2hυ) apresenta uma
perda bem pequena perda que é duas
vezes a freqüência da banda fundamental.
Freqüentemente a banda é bastante
pequena.

11. 11
Uma limitação final é requerida para completar o modelo. Na
ordem da luz absorvida uma molécula dipolar muda quando
ocorre transições. Por exemplo: H2 sempre tem dipolo igual zero
e não absorve luz infravermelho.
Contudo o HCl tem uma mudança de dipolo, isto acontece
quando o sinal do campo elétrico do feixe de luz é absorvido.
A intensidade de absorção esta relacionada com a magnitude
da carga do dipolo.

12. 12
SUMÁRIO
A freqüência (υ) e relação Constante da força (k) e massa (m)esta descrita
pela equação abaixo:
As moléculas somente absorvem quantidades quantizadas de energia.
A molécula absorve luz infravermelho de energia igual a hυ,
(fundamental), e a 2hυ (overtone).
Na ordem de absorção de luz infravermelho, absorve mais a molécula que possue
dipolo oscilante.
Moléculas com mais de dois átomos tem mais
complicações no espectro infravermelho.

13. 13
Cada modo normal está associado com
uma curva de energia potencial e
conseqüentemente com um valor de
nível de energia.
Existem quatro picos que indicam a
presença do CH2.

14. 14
MEDIÇÃO DO ESPECTRO INFRAVERMELHO
EXISTEM DOIS TIPOS DE ESPECTROFOTOMETROS INFRAVERMELHO:
CLÁSSICO ( DISPERSIVO ) E O MODERNO ( TRANSFORMADA DE FOURIER- FT )
O gráfico de resposta do detector versus
comprimento de onda, é chamado espectro. A
amplitude é convertida em percentual de luz
transmitida através da amostra e chamada de %T.

15. 15
VANTAGENS COM RELAÇÃO AO ESPECTROFOTOMETRO DISPERSIVO:
- O espectro pode ser obtido rapidamente porque todos os comprimentos de onda são medidos
simultaneamente.
- Amostras opacas ou refletidas podem ser utilizadas.
- A escala do numero de ondas é mais preciso porque esta internamente calibrado com LASER.
O espectro pode ser usado para identificar amostras
desconhecidas. A teoria da vibração molecular é usada para
interpretação dos espectros.