Este documento apresenta conceitos básicos sobre espectrometria UV-Vis, incluindo:
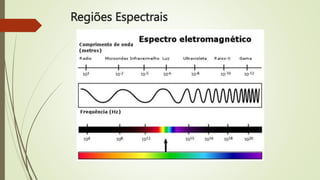
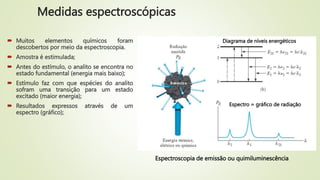
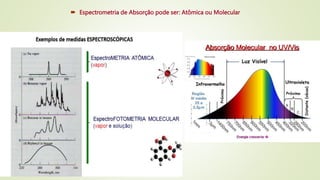
1) Definições de termos como espectrometria, métodos espectroscópicos e regiões espectrais;
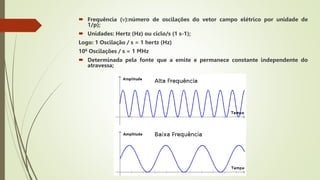
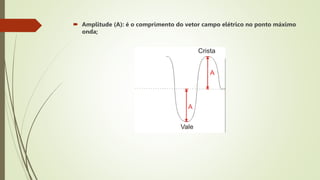
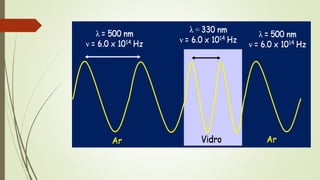
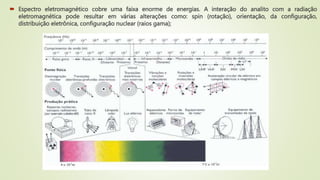
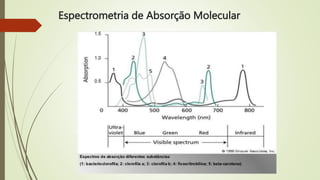
2) Propriedades da radiação eletromagnética como comprimento de onda e frequência;
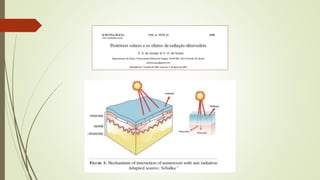
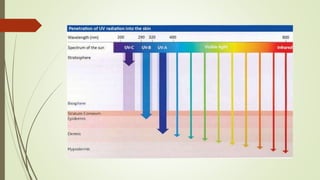
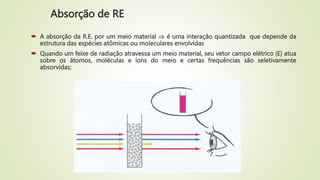
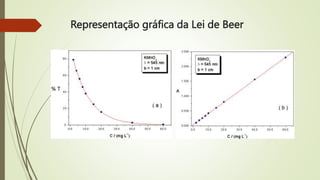
3) Processo de absorção da radiação e a Lei de Beer-Lambert que relaciona absorbância com concentração e caminho óptico.