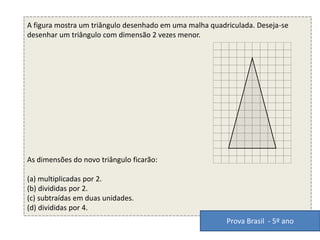
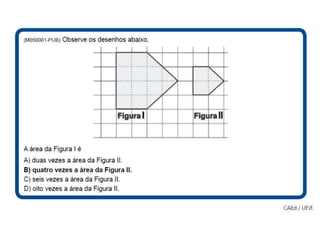
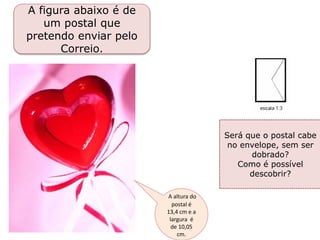
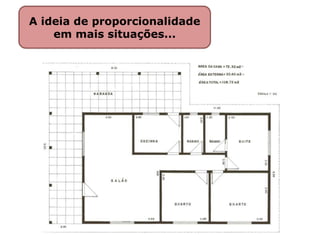
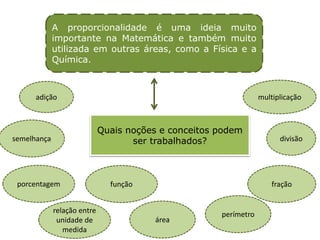
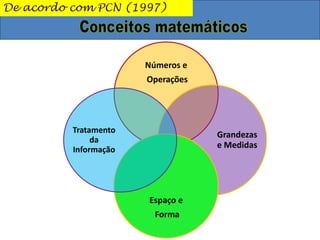
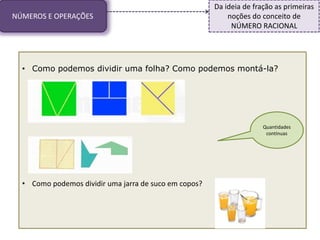
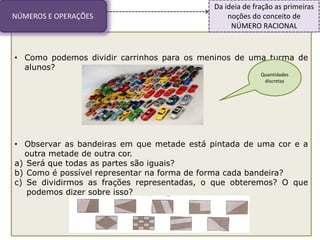
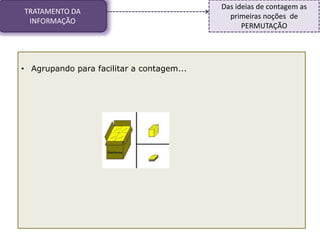
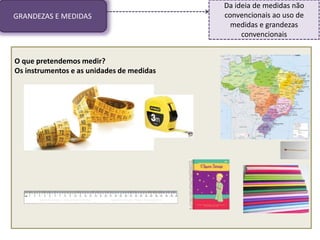
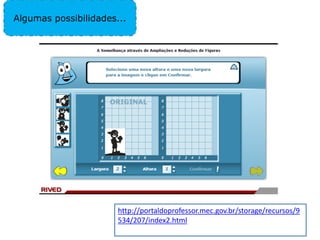
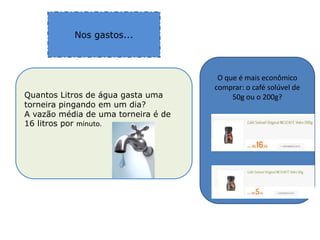
1) O documento discute conceitos matemáticos como proporcionalidade, frações e grandezas medidas que podem ser ensinados nos anos iniciais. 2) Inclui exemplos de atividades para introduzir esses conceitos de forma significativa para os alunos. 3) Reflete sobre como a aprendizagem da matemática nos anos iniciais deve levar em conta o desenvolvimento cognitivo das crianças e sua compreensão do mundo.

1. UNIJUÍ – UNIVERSIDADE REGIONAL DO NOROESTE DO ESTADO DO RIO
GRANDE DO SUL
Marta Cristina Cezar Pozzobon

2. VÍDEOS
1. Amarelinha
2. Proporcionalidade

3. Algumas possibilidades...
http://portaldoprofessor.mec.gov.br/storage/recursos/9
534/207/index2.html

4. Questão – Prova Brasil 2009

5. A figura mostra um triângulo desenhado em uma malha quadriculada. Deseja-se
desenhar um triângulo com dimensão 2 vezes menor.
As dimensões do novo triângulo ficarão:
(a) multiplicadas por 2.
(b) divididas por 2.
(c) subtraídas em duas unidades.
(d) divididas por 4.
Prova Brasil - 5º ano

7. A figura abaixo é de
um postal que
pretendo enviar pelo
Correio.
Será que o postal cabe
no envelope, sem ser
dobrado?
Como é possível
descobrir?
A altura do
postal é
13,4 cm e a
largura é
de 10,05
cm.

8. A ideia de proporcionalidade
em mais situações...

9. Em uma festinha cada criança levou 2 refrigerantes. Ao todo 8
crianças foram à festinha. Quantos refrigerantes havia?
8 crianças - ? Refrigerantes
Podemos dizer que a relação é: “1 está para 2, assim como 8
está para 16”. O resultado pode ser obtido multiplicando 8 por 2.
Paulo comprou 3 cadernos e pagou R$ 14,00. quanto pagaria de
tivesse comprado 6 cadernos desse tipos?
- R$ 14,00
6 cadernos - ?
Se em vez de 6 fosse 5, certamente precisaria encontrar o preço
de um caderno. Se ele comprar o dobro, precisará saber o dobro.

10. Nos gastos...
Quantos Litros de água gasta uma
torneira pingando em um dia?
A vazão média de uma torneira é de
16 litros por minuto.
O que é mais econômico
comprar: o café solúvel de
50g ou o 200g?

11. A proporcionalidade é uma ideia muito
importante na Matemática e também muito
utilizada em outras áreas, como a Física e a
Química.
Quais noções e conceitos podem
ser trabalhados?
adição multiplicação
divisão
porcentagem
semelhança
área
perímetro
fração
relação entre
unidade de
medida
função

12. Problematização/
Vivência
Formalização
do conceito
Ponto de partida da atividade matemática.

13. O fazer matemático nos anos iniciais:
Um ambiente para ensinar e aprender matemática;
O registro do aluno - processos de comunicação e
argumentação nas aulas de matemática /contribui na
elaboração de processos de abstração;
A interdisciplinaridade nos anos iniciais: a
matemática e outras áreas do conhecimento;
A produção de significados matemáticos.

14. De acordo com RCNEI(1998)
Noção de conservação
Noção de conjunto
Noção de fração
Noção de valor monetário
Noção de capacidade
Noção de tempo
Noção de cores e formas
 Noção de seriação
Noção de tamanho
Noção de distância
Noção de direção e sentido
Noção de massa

15. De acordo com PCN (1997)
Números e
Operações
Grandezas
e Medidas
Espaço e
Forma
Tratamento
da
Informação

16. NÚMEROS E OPERAÇÕES
Da ideia de fração as primeiras
noções do conceito de
NÚMERO RACIONAL
• Como podemos dividir uma folha? Como podemos montá-la?
• Como podemos dividir uma jarra de suco em copos?
Quantidades
contínuas

17. • Como podemos dividir carrinhos para os meninos de uma turma de
alunos?
• Observar as bandeiras em que metade está pintada de uma cor e a
outra metade de outra cor.
a) Será que todas as partes são iguais?
b) Como é possível representar na forma de forma cada bandeira?
c) Se dividirmos as frações representadas, o que obteremos? O que
podemos dizer sobre isso?
Quantidades
discretas
NÚMEROS E OPERAÇÕES
Da ideia de fração as primeiras
noções do conceito de
NÚMERO RACIONAL

18. TRATAMENTO DA
INFORMAÇÃO
Das ideias de contagem as
primeiras noções de
PERMUTAÇÃO
• Contar oralmente, comparar quantidades...
• Formar coleções de objetos, descobrir a quantidade de objetos da
coleção, registrar a quantidade da coleção.
• Registro a partir de formas de organizar a coleção.

19. TRATAMENTO DA
INFORMAÇÃO
Das ideias de contagem as
primeiras noções de
PERMUTAÇÃO
• Agrupando para facilitar a contagem...

20. TRATAMENTO DA
INFORMAÇÃO
Das ideias de contagem as
primeiras noções de
PERMUTAÇÃO
• Quantas palavras diferentes (com ou sem sentido) você pode
formar, usando as letras da palavra AMOR?

21. ESPAÇO E FORMA
Das ideias de objetos que
rolam/não rolam as primeiras
noções do conceito de
tridimensionalidade
• Separar objetos que rolam e que não rolam, observando suas características.
• Relacionar com objetos conhecidos.
Pirâmide de Quéops. Fonte: site Webshots

22. ESPAÇO E FORMA
Das ideias de objetos que
rolam/não rolam as primeiras
noções do conceito de
tridimensionalidade
• Manusear embalagens e agrupá-las de acordo com diferentes critérios, a partir das
características.
• Construir brinquedos com as embalagens.
• Criar sólidos com massa de modelar.
• Distinguir os elementos dos poliedros (faces, vértices e arestas) e o número de cada
um deles. Identificar as faces paralelas (faces opostas) em um cubo.
• Planificar sólidos .
• Observar padrões e regularidades, percebendo a relação entre o número de vértices,
faces e arestas.
• Fórmula de Euler: V + F = A + 2

23. GRANDEZAS E MEDIDAS
Da ideia de medidas não
convencionais ao uso de
medidas e grandezas
convencionais
• “Quantas vezes é maior?”, “Qual a distância?”, “Qual é o peso?”
• Medir usando passos, mãos, barbantes...;
• Comparações de comprimentos, alturas, pesos e
capacidades: Perto/longe, mais baixo/mais
alto, muito/pouco, grande/pequeno.
• Medindo tamanhos usando palmos, barbante, no chão, de pé...

24. GRANDEZAS E MEDIDAS
Da ideia de medidas não
convencionais ao uso de
medidas e grandezas
convencionais
• Medindo a sala...

25. GRANDEZAS E MEDIDAS
Da ideia de medidas não
convencionais ao uso de
medidas e grandezas
convencionais
O que pretendemos medir?
Os instrumentos e as unidades de medidas

26. O que se tem ensinado de matemática?
O ensinamos têm produzido aprendizagens
significativas? Estão de acordo com as demandas
atuais?
Por que ensinar e como ensinar?
Como o LD pode colaborar com o
processo de aprendizagem do aluno?