ESTRUTURAS

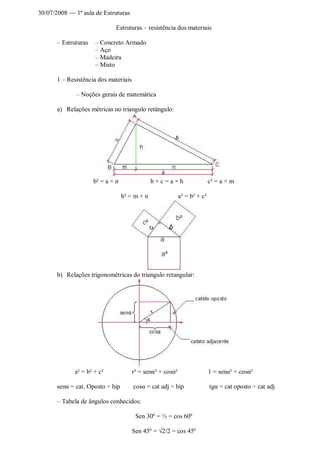
1. 30/07/2008 1ª aula de Estruturas
Estruturas – resistência dos materiais
– Estruturas – Concreto Armado
– Aço
– Madeira
– Misto
1 – Resistência dos materiais
– Noções gerais de matemática
a) Relações métricas no triangulo retângulo:
b² = a × n b × c = a × h c² = a × m
h² = m × n a² = b² + c²
b) Relações trigonométricas do triangulo retangular:
a² = b² + c² r² = senα² + cosα² 1 = senα² + cosα²
senα = cat. Oposto ÷ hip cosα = cat adj ÷ hip tgα = cat oposto ÷ cat adj
– Tabela de ângulos conhecidos:
Sen 30º = ½ = cos 60º
Sen 45º = √2/2 = cos 45º

2. Sen 60º = √3/2 = cos 30º
Sen 0º = 0 cos 0º = 1
Sen 90º = 1 cos 90º = 0
c) Relações trigonométricas de um triangulo qualquer:
Leis dos cossenos:
c² = a² + b² + 2 × a × b × cos θ
b² = a² + c² + 2 × a × c × cos α
a² = b² + c² + 2 × b × c × cos
Lei dos senos:
a
=
B
=
C
sen senα senθ
Operações Vetoriais
Objetivo: obter a resultante dos vetores:
– Conceito: Vetor é um elemento unitário que tem: origem, sentido e direção.
a) Soma de dois vetores de mesmo sentido e mesma direção:
R = a + b
b) Soma de dois vetores de mesma origem, direção e sentido diferente:
R = | a + b|
c) Soma de dois vetores quaisquer:
Processo geométrico para obter a resultante final:

3. Processo analítico:
R = √(a)² + (b)² + 2 × a × b × cosα
Outras situações:
31/07/2008 2ª aula de Estruturas
Quanto maior o ângulo maior a força.
– Decomposição de vetores:
Conceito: conhecendo à resultante determinaremos através da trigonometria as
componentes vetoriais.
Exemplo 1 Exemplo 2
Senα = cat. oposto ÷ hip senα = V ÷ R V = R × senα
Cosα = cat. adj ÷ hip cosα = H ÷ R H = R × cosα
Exercícios:
1) Determinar as resultantes vetoriais:
a) onde: a = 3 b = 2 R = 5
b) a = 15T b = 10T R = 5T

4. c) onde: V = 8m H = 10m R = 12,81 m
R = √8² + 10²
R = √64 + 100
R = √164
R = 12,81 m
d) onde: a = 5T b = 8T
R = √(a)² + (b)² + 2 × a × b × cosα
R = √(5)² + (8)² + 2 × 5 × 8 × cos60º
R = √ 25 + 64 + 80 × 0,50
R = √ 89 + 40
R = √ 129
R = 11,36 T
2) Calcular as componentes vetoriais:
Onde: R = 100 T α = 30º
H = R × cos 30
H = 100 × 0,866
H = 86,60 T
V = R × sen 30º
V = 100 × 0,5
V = 50 T
3) Calcular a intensidade dos cabos de aço F1 e F2:
a)
V = F1 × sen30º
F1 = V ÷
sen30º
F1 = 2,5 ÷
0,50
F1 = 5T
b)

5. F1 = V ÷ sen60º
F1 = 2,5 T ÷ 0,866
F1 = 2,89 T
06/08/2008 3ª aula de Estruturas
Aplicação de decomposição vetorial
Exercício: Determinar as forças atuantes nos cabos bem como indicar qual está sendo
tracionado e comprimido.
R = V ÷ sen45º
R = 20T ÷ 0,707
R = 28,28T
H = R × cos 45º
H = 28,28 T × 0.707
H = 20 T

6. F1 = V ÷ sen60º = 50 T ÷ 0,866 = 57,73 T
F2 = V ÷ sen60º = 50 T ÷ 0,866 = 57,73 T
Unidades de conversão
Massa 1 T = 1000 kg = 10³ kg
Comprimento 1 m = 100 cm = 10–
² kg
Força 1 kgf = 9,8 N ≈ 10 N
Solicitações:
a) Tração:
b) Compressão:
c) Cizalhamento (corte):
d) Flexão:
e) Torção:
– Tensão Normal ( )
Tensão = F(força) ÷ S (superfície)
= F ÷ S

7. Unidade da tensão pode ser em:
T/m²; T/cm²; kgf/m; kgf/mm²; N/m²; N/cm²
Exercícios:
a) F = 500 kgf S = 4 cm²
= 500 kgf ÷ 4 cm² = 125 kgf/cm²
b) F = 4000 kgf Secção quadrada c/ 4 mm de lado
= 4000 kgf ÷ 16 mm² = 250 kgf/mm²
c) F = 90 N Ø = 3 mm
S = × Ø² ÷ 4 = 3,1416 × (3²) ÷ 4 = 7,07 mm²
= 90 N ÷ 7,069 mm² = 12,73 N/mm²
2) Qual é a força aplicada em um corpo que tem área da secção transversal à 0,5 cm²,
um desenvolveu uma tensão de 800 N/cm².
= F ÷ S 800 N/cm² = F ÷ 0,5 cm² F = 400 N
3) Qual deverá ser o Ø de uma barra sujeira a uma tensão de 1400 kgf/cm², sabendo–se
que a força aplicada é de 700 kgf?
= F ÷ S 1400 kgf/cm² = 700 kgf ÷ S S = 700 kgf ÷ 1400 kgf/cm² = 0.5 cm²
Ø = 2 √ S ÷ = 2 √ 0,5 ÷ 3,1416 = 2 √ 0,159 = 2 × 0,399 = 0,798
4) Qual é o volume de concreto para ser utilizado em um reservatório de forma cilíndrica
conforme projeto abaixo:
SD = × Ø² ÷ 4 = 3,1416 × (2,5)² ÷ 4 = 4,909 m²
Sd = × Ø² ÷ 4 = 3,1416 × (2,3)² ÷ 4 = 4,909 m²
SC = D – d = 4,909 – 4,155 = 0,754 m²
Laje:
VL = B × h = 4,909 m² × 0,20 m = 0,982 m³
Reservatório:
VR = SC × h = 0,754 m² × 2,80 m = 2,111 m³

8. VTOTAL = VL + VR = 2,111 m³ + 0,982m³ = 3,093 m³ de concreto
5) Calcular o volume de concreto a ser utilizado para preencher as 28 estacas de fundação
de um sobrado, sabendo–se que o diâmetro das mesmas é de 25 cm e o comprimento de cada
uma é 12 m.
Área da base da estaca:
SESTACA = 3,1416 × (0,25)² ÷ 4 = 0,049 m²
Distâncias das estacas:
38 estacas × 12 m = 456 m
VESTACA = SESTACA × h
VESTACA = 0,049 m² × 456 m = 22,344 m³ de concreto
Para achar o Ø:
S = × Ø² ÷ 4 ز = 4 × S ÷ Ø = √ 4 × S ÷ Ø = 2 η√ S ÷
Resumo de formulas sobre tensão:
Principal:
= F ÷ S
Auxiliares:
SO = × Ø² ÷ 4 e Ø = 2 √ S ÷
Solicitação à tração
Diagrama (Tensão × Deformação)
– Tração elástica + usada
– Tração deformação
– Tração de ruptura
Região 1 elástica
Região 2 plástica

9. Região 3 ruptura
P = tensão de proporcionalidade
e = Tensão de escoamento
r = Tensão de resistência máxima
rup = Tensão de ruptura
ε = Deformação
Hoock – físico
CA 50 A
/B
CA Concreto Armado
50 Capacidade nominal (5000 kg/cm²)
A
/B A – Produção a frio e B – Produção a quente
Incêndios em SP
1º Edifício Andraus – não precisou ser demolido – Construído CA 42 B
2º Edifício Joelma – não precisou ser demolido – Construído CA 42 B
3º Edifício novo Telesp – precisou ser demolido – Construído CA 50 A
CA 50 SS para suportar calor e solda
Treliça: CA 50 SS e CA 60 SS
Resistência de calculo do aço Resistência do concreto
Fcy =
Capacidade nominal
Fck =
Carga pilar
1,15 1,15
Carga real + 40% (pilar)
Lei de Hoock
Tgα = senα ÷ cosα tgα = ÷ ε E = ÷ ε
E = Modulo de elasticidade
= Tensão Nominal
ε = Deformação
Relações de formulas:
= F ÷ S = E × ε
F ÷ S = E × ε
– Deformação (ε)
a) Solicitação á tração:

10. Onde: l0 = Comprimento inicial
Δl = Variação do comprimento
lf = Comprimento final
lf = l0 + Δl
ε = Δl ÷ l0 ou ε% = Δl ÷ l0 × 100
b) Compressão (encurtamento)
lf = l0 – Δl
ε = Δl ÷ l0 ou ε% = Δl ÷ l0 × 100
relacionamento de formulas
F ÷ S = E × ε e ε = ε = Δl ÷ l0
Tal quie:
F ÷ S = Δl ÷ l0 × E Δl = (F × l0) ÷ ( E × S)
Resumo geral de formulas:
Principais:
= F ÷ S ε = Δl ÷ l0 ε = Δl ÷ l0 × 100 Δl = (F × l0) ÷ ( E × S) = E × ε
Formulas auxiliares:
Circulo Retangulo Trapézio Triangulo
S0 =
× Ø²
SRET = b × h STP =
(B + b) × h
S =
b × h
4 2 2
Quadrado Lozango Coroa Diâmetro
S = l² SLOZ =
D × d
SCOROA =
(R² – r²)
Ø = 2√ S/
2
Alguns módulos de Elasticidade (E)

11. Aço E = 2.100.000 kg/cm²
Cobre E = 1.200.000 kg/cm²
Alumínio E = 700.000 kg/cm²
Concreto E = 300.000 kg/cm²
Exercícios:
a) Determinar a deformação percentual de um fio que tinha comprimento inicial de 80 cm
e final de 82 cm.
lf = l0 + Δl 82 = 80 + Δl Δl = 2 cm
ε% = Δl ÷ l0 × 100 = (2 ÷ 80) × 100 = 2,5 %
b) Qual o comprimento inicial de um corpo que teve uma deformação igual a 1%.
Sabendo–se que o corpo inicial é de 120 mm.
ε = Δl ÷ l0 ε = Δl ÷ lf – Δl 0,01 = Δl ÷ 120 – Δl 0,01 × 120 – Δl = Δl
Δl = 1,2 – 0,01 Δl Δl + 0,01 Δl = 1,2 Δl = 1,2 ÷ 0,01 Δl = 1,2 ÷ 1,01 = 1,188 mm
l0 = lf – Δl = 120 mm – 1,188 mm = 118,81 mm
c) Qual o comprimento final de um corpo que tem deformação igual a – 0,02 e
comprimento de 600 mm.
ε = Δl ÷ l0 0,02 = Δl ÷ 600 m Δl = 12 mm
lf = l0 – Δl = 600 – 12 = 588 mm
d) Qual o alongamento e comprimento final de um fio de aço, submetido a uma carga de
tração de 1000 kgf com comprimento inicial de 60 cm e seção transversal igual a 0,5 cm²
Δl = (F × l0) ÷ ( E × S) = (1000 kgf × 60 cm) ÷ (2.100.000 kgf/cm²× 0,5 cm²)
Δl = 60×10³ cm ÷ 1.05×106
= 57,143×10–3
= 0,057 cm
lf = l0 – Δl = 60 cm + 0,057 cm = 60,057 cm
e) Dado o esquema abaixo determinar o diâmetro do fio sabendo–se que o alongamento
do conjunto é de 1 mm.
E = 2.100.000 kgf/cm²
Ø = ?
F = 1.200 kgf
Δl = 1 mm 0, 1 cm
l0 = 200 cm
Δl = (F × l0) ÷ ( E × S) 0,1 = (1200 kgf × 200 cm) ÷ (2.100.000 kgf/cm²× S)

12. S = (1200 kgf × 200 cm) ÷ (2.100.000 kgf/cm² × 0,01 cm) = 24 cm ÷ 21 cm = 1,143 cm²
Ø = 2 √ S ÷ = 2 √ 1,143 ÷ 3,1416 = 2 √ 0,364 = 2 × 0,603 = 1,206 cm
21/08/2008 4ª aula de Estruturas
f) dado o esquema abaixo, determinar o alongamento de cada fio, deformação percentual
e a tensão:
Fio de aço:
ℓ0 = 600 mm 60 cm
Ø = 5 mm 0,5 cm
F = P = 1,5 T = 1500 kg
E = 2.100.000 kg/cm²
S = 0,916 cm²
S = × Ø² ÷ 4 = 3,1416 × (0,5)² ÷ 4 = 0,916 cm²
Δℓ = (F × l0) ÷ ( E × S) = (1500 kg × 60 cm) ÷ (2.100.000 kg/cm² × 0,1964 cm²)
Δℓ = 90 cm ÷ 412,335 = 0,2183 cm
ε = Δℓ ÷ ℓ0 × 100 = 0,2183 cm ÷ 60 cm × 100 = 0,36 %
= F ÷ S = 1500 kg ÷ 0,1964 cm² = 7.637,47 gk/cm²
Fio de cobre:
ℓ0 = 40 cm
Ø = 8 mm 0,8 cm
F = P = 1,5 T = 1500 kg
E = 1.200.000 kg/cm²
S = 0,503 cm²
S = × Ø² ÷ 4 = 3,1416 × (0,8)² ÷ 4 = 0,503 cm²
Δℓ = (F × ℓ0) ÷ ( E × S) = (1500 kg × 40 cm) ÷ (1.200.000 kg/cm² × 0,503 cm²)
Δℓ = 60 cm ÷ 603,6 = 0,099 cm
ε = Δℓ ÷ ℓ0 × 100 = 0,099 cm ÷ 40 cm × 100 = 0,25 %
= F ÷ S = 1500 kg ÷ 0,1964 cm² = 7.637,47 gk/cm²
27/08/2008 5ª aula de Estruturas
Vigas e Flexão Simples

13. – Considerações solicitação de flexão:
Solicitação que tende a modificar (curvar) o eixo longitudinal de uma barra, devido a
aplicação de um conjunto de forças normais (perpendicular ao eixo da viga).
Estribo tem duas funções: arme e desarme. Distanciamento máximo é de 20 cm.
Quanto mais aumenta a carga mais a linha sobe
Só põe as costelas quando a altura da viga passar de 50 cm.
Vinculações
a) Apoio Móvel:
ou
b) Apoio fixo:
c) Engastamento
03/09/2008 6ª aula de Estruturas
1º vinculo: Apoio móvel: (Apoio Simples)

14. Permite
– Deslocamento horizontal
– Giro no apoio
Não permite:
– Deslocamento vertical
Tem somente 1 grau de vinculação
2º Vinculo: Apoio Simples
Permite:
– Giro no apoio
Não permite:
– Deslocamento vertical e horizontal
Apoio simples que tem 2 graus de vinculação
3º Vinculo: Engastamento
Permite:
–Não tem liberdade (não permite nada)
Tem 3 graus de vinculação
– Denominação das vigas
a) Vigas bi apoiadas:
b) Vigas isostáticas bi apoiadas com balanço:
ou
c) Vigas em balanço (isostática):

15. d) Vigas Continuas (Hiperistaticas):
Contem ou estão sobre mais de dois apoios simples:
– Tipos de cargas nas estruturas
a) Cargas Permanentes
– Cargas Concentradas
– Cargas Distribuídas
– Cargas Variáveis
– Cargas Mistas
Ex. peso próprio da viga
b) Cargas Acidentais:
So aquela que ocorrem eventualmente
– Pessoas sobre a laje
– Ação do vento
– Tipos de Carregamento
a) Cargas Concentradas (cargas pontuais):
Unidades: kg (kgf); T (Tf); N
b) Cargas Distribuídas:
São cargas aplicadas ao longo de toda a viga ou em parte dela e podem ser:
b1)Carga Uniformemente distribuída:
ou
Unidades do (q):

16. kgf/cm; kgf/m; Tf/m etc.
b2) Cargas Distribuída variável:
b3) Cargas Mistas:
04/09/2008 7ª aula de Estruturas
– Conceito de momento de uma força
Momento é o produto de intensidade da força pela distância até o ponto estudado.
M = F × d
kgf × m; kgf × cm; Tf × m
Conversão de sinais:
a) Para momento:
b) Forças Verticais:
c) Forças Horizontais:
Reações de apoio

17. Para evitar a fissura na laje tem que por a malha
A – Vigas Bi Apoiadas.
A1 – Com uma carga concentrada em um ponto qualquer do vão.
Formulas:
– Reação de apoio:
RA =
P × b
e RB =
P × a
ℓ ℓ
– Momento Fletor
MC = RA× a ou MC = RB × b
Exercício:
Dado o esquema de carga abaixo, determinar todos os esforços e traçar as respectivas
linhas de estado.

18. Reação de apoio:
RA = (P × b) ÷ ℓ = (18T × 4 m) ÷ 6 m = 12 T
RB = P – RA = 18 T – 12 T = 6 T
Momento Fletor
MC = RA × a = 12 T × 2 m = 24 T×m
A2 – Viga bi apoiada com duas cargas concentradas iguais e equilibradas.
Reações de apoio (Q)
RA = RB = P
Momento Fletor
MC = MD = RA × a = RB × a
Obs. Transpasse no mínimo 50 cm.
Pela norma o transpasse é calculado pegando o Ø do ferro × 80 vezes mais grosso.
A3 – Viga Bi Apoiada com carga distribuída uniformemente ao longo do vão.

19. Formulas
Reações de apoio
RA = RB =
q × ℓ
2
Momento Fletor
MMAX =
q × ℓ²
8
Carregamento distribuído
Unidades:
q (T/m; kg/m; T/cm ...)
Tijolos cerâmicos:
X = 1.300 kg/m³
γ = 1.400 kg/m³
Parede: 0,22 m × 3,00 m × 1,00 × (1.400 kg/m³)
Parede: 924 kg/m
PTOTAL: 924 kg/m × 8 m = 7.392 kg

20. Exercício: Dado o esquema de carga da estrutura abaixo, calcular todos os esforços e
traçar os gráficos:
Solução da viga C – D:
Reação de apoio:
RD = (q × ℓ) ÷ 2 = (2 T/m × 6 m) ÷ 2 = 6 T
RC = (q × ℓ) ÷ 2 = (2 T/m × 6 m) ÷ 2 = 6 T
Momento Fletor:
MMAX = (q × ℓ²) ÷ 8 = (2 T/m × (6 m)²) ÷ 8 = 9 T.m
Solução viga 2 – Viga A – B

21. Reação de apoio:
RA = (P × b) ÷ ℓ = (6 T × 4m) ÷ 6 m = 4 T
RB = (P × a) ÷ ℓ = (6 T × 2m) ÷ 6 m = 2 T
Momento Fletor:
Mf = RA × a = 4 T × 2 m = 8 T.m
Mf = RB × b = 2 T × 4 m = 8 T.m
Solucionando a viga A – B:

22. Reação de apoio:
RA = (P × b) ÷ ℓ = (10 T × 6m) ÷ 8 m = 7,50 T
RB = (P × a) ÷ ℓ = (10 T × 2m) ÷ 8 m = 2,50 T
Momento Fletor:
Mf = RA × a = 7,50 T × 2 m = 15 T.m
Mf = RB × b = 2,5 T × 6 m = 15 T.m
Solucionando a viga C – D:
Reação de apoio:
RC = (P × b) ÷ ℓ = (10,5 T × 3m) ÷ 6 m = 5,25 T
RD = (P × a) ÷ ℓ = (10,5 T × 3m) ÷ 6 m = 5,25 T
Momento Fletor:
Mf = RA × a = 5,25 T × 3 m = 15,75 T.m
Mf = RB × b = 5,25 T × 3 m = 15,75 T.m
1 m³ de terra = 2.100 kg

23. Pilar acima de 20 cm os ferros com espaço de 20 cm.
B – Vigas em balanço:
B1 – Viga em balanço com uma carga concentrada na extremidade livre.
Formulas:
– Reação de apoio:
RA = P
Momento Fletor:
MA = – P × ℓ
O empuxo da água tem mais força a H/3 da altura do muro, num ângulo de 30º
B2 – Viga em balanço com carga distribuída.
Formulas:
– Reação de apoio:
RA = q × ℓ
Momento Fletor:
MA =
(– q × ℓ)
2
08/10/2008 8ª aula de Estruturas
Exercícios sobre Vigas em balanço:
Dado os esquemas abaixo; determinar todos os esforços e traçar os respectivos gráficos.
a) b) c)
a)

24. Reação de apoio:
RA = P = 8 T
Momento Fletor:
MA = – P × ℓ = 8 T × 2 m = 16 T.m
b)
Reação de apoio:
RA = q × ℓ = 2 T/m × 1,5 m = 3 T
Momento Fletor:
MA = (– q × ℓ²) ÷ 2 = (– 2T/m × (1,5 m)²) ÷ 2 = – 2,25 T.m
c)
Reação de apoio:

25. RA = P + P1 = 2 T + 2T = 4 T
Momento Fletor:
MA1 = –P × ℓ = – 2 T × 2 m = – 4 T.m
MA2 = –P × ℓ = – 2 T × 4 m = – 8 T.m
MAF = MA1 + MA2 = – 4 T.m + (– 8 T.m) = – 12 T.m
C – Vigas com um engaste e um apoio
C1 – Com carga concentrada em um ponto qualquer do vão.
Reações de apoio
RA=
P
×
3b
–
b³
2 ℓ ℓ³
RB=
P
× 2 –
3b
–
b³
2 ℓ ℓ³
Momento Fletor
MA=
– P × b (ℓ² - b²)
2 × ℓ²
MC= RB × b=
P × b
2 –
3b
+
b³
2 ℓ ℓ³
C2 – Viga com um apoio e um engaste com carga uniformemente distribuída ao longo do
vão.
Formulas
Reações de apoio
RA = 0,6 × q × ℓ
RB = 0,4 × q × ℓ
Qx= – q × ℓ
3
–
x
8 ℓ
Momentos Fletores
MA = – q × ℓ²
8
MMAX = 0,07 × q × ℓ²
MX = q × ℓ × x 3 – x
2 4 ℓ
D – Vigas com dois engastes
D1 – Com uma carga concentrada em um ponto qualquer do vão.

26. Reações de apoio
RA=
P×b
× 1 –
a²
+
a × b
= P – RB
2 ℓ² ℓ³
RB=
P×a
× 1 –
b²
+
a × b
= P – RA
2 ℓ² ℓ³
Momento Fletor
MA=
– P × a × b²
ℓ²
MB=
– P × b × a²
MC =
2 × P × a² × b²
ℓ² ℓ³
D2 – Vigas com dois engastes com carga uniformemente distribuída ao longo do vão:
Formulas
– Reações de Apoio
RA = RB =
Q × ℓ
2
QX = – (RB – q × ℓ)
Momentos Fletores
MA = MB = –
q × ℓ²
12
MMAX =
q × ℓ²
24
MX = q × ℓ 1
–
x
+
x²
2 6 ℓ ℓ²
23/10/2008 9ª aula de Estruturas
Vigas Continuas
São vigas que possuem mais de dois pontos, são consideradas como vigas hiperistaticas.
Essas vigas são solucionadas pelos métodos:
– De cross;
– Equação dos três momentos;
– Ou através de vigas isoladas com coeficiente de aproximação.
Exemplo:
Resultados Finais
a) Reações de apoio:

27. RAF = RA
RBF = (RB1 + RB2)
RCF = RC
b) Momentos Fletores:
MF (+) = (+) MMAX1
MBF = – (MB1 + MB2) × 0,8
MDF = MD (+)
Exercícios: Calcular todos os esforços parciais e finais, bem como os gráficos parciais e
finais da viga abaixo:
Solucionando a viga 1:
Reações de apoio:
RA = P = 3T
Momento Fletor:
MA1 = – P × ℓ = – 3 T × 1,5 m = – 4,5 T.m
Solucionando viga 2:
Reações de apoio:
RA2 = RB1 = (q × ℓ) ÷ 2 = (3 T/m × 6m) ÷ 2 = 9 T
Momentos Fletores:
MA2 = MB2 = – (q × ℓ²) ÷ 12 = – (3 T/m × (6 m)²) ÷ 12 = – 9 T.m

28. MMAX = – (q × ℓ²) ÷ 24 = – (3 T/m × (6 m)²) ÷ 24 = – 4,5 T.m
Solucionando a viga 3:
Reação de apoio:
RB2 = P = 6T
Momento Fletor:
MB2 = – P × ℓ = – 6 T × 2,5 m = – 15 T.m
Resultados Finais:
Reações de apoio:
RAF = (RA1 + RA2) = 3 T + 9 T = 12 T
RBF (RB1+ RB2) = 9 T + 6 T = 15 T
Momentos Fletores:
MAF = – (MA1 + MA2) × 0,8 = – (4,5 T.m + 9 T.m) × 0,8 = – 10,80 T.m
MBF = – (MB1 + MB2) × 0,8 = – (9 T.m + 15 T.m) × 0,8 = – 19,20 T.m
MMAXF = + MMAX = + 4,5 T.m
30/10/2008 10ª aula de Estruturas
Pilares
São elementos estruturais que recebe as cargas provenientes das vigas e as transferem
para as fundações.
Também serve para dar estabilidade e forma a arquitetura da obra.
Obs.: A perda de resistência do pilar chama–se “Flambagem” (λ)
λ ≤ 40 – Pilar Robusto
40 ≤ λ ≤ 80 – Pilar Esbelto
λ > 80 – Pilar Perigoso (Requer novo calculo)
Pilar flambou Fissura no meio da parede
Argamassa ruim Tirinhas na tinta
– Eixo dos pilares:

29. ℓf = Comprimento de flambagem;
k = Coeficiente de flambagem
O = Vinculo de rotulo
4 = Pórtico (estrutura hiperistática)
– Coeficiente de flambagem:
Onde: ℓf Comprimento flambagem
k Coeficiente k
I Momento de inércia dos eixos
A×C Área do concreto
– Momentos de Inércia dos eixos:
Ixx =
b × h³
(cm4
) Iyy =
H × b³
(cm4
)
12 12
05/11/2008 11ª aula de Estruturas
Exemplos (Pilares)
– Determinação do coeficiente de flambagem (λ)
– Calcular o coeficiente de flambagem para um pilar com 3,20 m de comprimento, com
seção de (15 × 30) cm com engaste no pé rotulo superior.
Secção:
a) Área da Secção (AC)
AC = b × h = 15 cm × 30 cm = 450 cm²
b) Momentos de Inércia:
IXX = (b × h³) ÷ 12 = ((30 cm × (15 cm)³) ÷ 12 = 8.437,50 cm4
IYY = (h × b³) ÷ 12 = ((15 cm × (30 cm)³) ÷ 12 = 33.750 cm4
c) Coeficiente de flambagem (λ):
λX = (ℓf × K) ÷ √(IXX ÷ AC) = (320 cm × 0,7) ÷ √ (8.437,50 cm4
÷ 450 cm²)

30. λX = 224 cm ÷ √ 18,75 cm² = 224 cm ÷ 4,33 cm = 51,73
λY = (ℓf × K) ÷ √(IYY ÷ AC) = (320 cm × 0,7) ÷ √ (33.750 cm4
÷ 450 cm²)
λY = 224 cm ÷ √ 75 cm² = 224 cm ÷ 8,66 cm = 25,87
d) Análise Final:
Eixo XX = λX = 51,73 Esbelto (40 < 51,73 < 80)
Eixo YY = λY = 25,87 Robusto (25,87 < 40)
Exemplo 2
Calcular o coeficiente de flambagem, bem como verificar sua resistência em relação aos
eixos.
Esquema: Seção:
a) Área da Seção (AC):
AC = b × h = 20 cm × 20 cm = 400 cm²
b) Momentos de Inércia:
IXX = (b × h³) ÷ 12 = ((20 cm × (20 cm)³) ÷ 12 = 13.333,33 cm4
IYY = (h × b³) ÷ 12 = ((20 cm × (20 cm)³) ÷ 12 = 13.333,33 cm4
c) Coeficiente de flambagem (λ):
λX = (ℓf × K) ÷ √(IXX ÷ AC) = (340 cm × 1) ÷ √ (13.333,33 cm4
÷ 400 cm²)
λX = 340 cm ÷ √ 33,33 cm² = 340 cm ÷ 5,77 cm = 58,93
λY = (ℓf × K) ÷ √(IYY ÷ AC) = (340 cm × 1) ÷ √ (13.333,33 cm4
÷ 400 cm²)
λX = 340 cm ÷ √ 33,33 cm² = 340 cm ÷ 5,77 cm = 58,93
d) Análise Final:
Eixo XX = λX = 58,89 Esbelto (40 < 58,89 < 80)
Eixo YY = λY = 58,89 Esbelto (40 < 58,89 < 80)
06/11/2008 12ª aula de Estruturas
Ferragem Mínima para os pilares

31. – Diâmetro mínimo = Ø 10 mm ou (3
/8”)
ASMIN = 0,8 % × AC
AS Armadura longitudial
AC Seção Transversal do Pilar
– Armadura Transversal (Estribos):
– Espaçamento máximo = 20 cm
AS = Ø 10 mm Estribos 1 Ø 6,3 mm (1
/4”) c/ 15 cm
AS = Ø 12,5 mm Estribos 1 Ø 6,3 mm (1
/4”) c/ 20 cm
– FckMIN = 20 MPa
Exemplo: Baseado nos exercícios de 05/11/2008
a) Pilar seção (15 × 30 cm)
AC = 15 cm × 30 cm = 450 cm²
a1) Seção mínima de aço (AS)
ASmin = 0,8% × AC = 0,008 × 450 cm² = 3,6 cm² – 6 Ø 10 mm
– 4 Ø 12,5 mm
O Pilar:
e 5 ≤ e ≤ 20 cm o ideal é: 10 ≤ e ≤ 20 cm
b) Pilar Seção (20 × 20 cm)
AC = 20 cm × 20 cm = 400 cm²
b1) Seção mínima de aço (AS):
ASmin = 0,8 % × AC = 0,008 × 400 cm² = 3,2 cm² – 6 Ø 10 mm

32. – 4 Ø 12,5 mm
O Pilar:
6 Ø 10,0 mm
(4,26 cm²)
4 Ø 12,5 mm
(5,07 cm²)
– Calcular tudo do Pilar
ℓf = 3,40 m
k = 1
a) Área da Seção:
AC = 2 × [((B + b) ÷ 2) × h)] = 2 × [((35 + 20) ÷ 2) × 18)] = 2 × 495 = 990 cm²
b) Momentos de Inércia:
IXX = (b × h³) ÷ 12 = ((35 cm × (20 cm)³) ÷ 12 = 136.080 cm4
IYY = (h × b³) ÷ 12 = ((20 cm × (35 cm)³) ÷ 12 = 128.625 cm4
c) Coeficiente de flambagem (λ):
λX = (ℓf × K) ÷ √(IXX ÷ AC) = (340 cm × 1) ÷ √ (136.080 cm4
÷ 990 cm²)
λX = 340 cm ÷ √ 137,45 cm² = 340 cm ÷ 11,72 cm = 29
λY = (ℓf × K) ÷ √(IYY ÷ AC) = (340 cm × 1) ÷ √ (128.625 cm4
÷ 990 cm²)
λX = 340 cm ÷ √ 129,92 cm² = 340 cm ÷ 11,40 cm = 29,83
d) Análise Final:
Eixo XX = λX = 29,00 Robusto (29 < 40)
Eixo YY = λY = 29,83 Robusto (29,83 < 40)
e) Seção mínima do Aço (AS)
AS = 0,8% × AC = 0,008 × 990 cm² = 7,92 cm² – 6 Ø 16 mm (3
/8”)
12/11/2008 13ª aula de Estruturas
Blocos de Fundações

33. – Conceito: São elementos de infra–estrutura, que atuam como distribuidor das cargas
provenientes dos pilares para as estacas, além de absorver os esforços de torção provenientes das
vigas baldrames.
– Os blocos poderão ser para até 7 estacas;
– Condições construtivas dos blocos:
Onde: h = altura útil h ≥ 45 cm
d = altura útil d ≥ 50 cm
r = proteção da estaca r ≥ 5 cm
CA = Cota de Arrasamento da estaca
– Armaduras mínimas:
– Ferro principal (longitudinal) Ø 10 mm
– Estribos Longitudinais e transversais Ø 8 mm
– Concreto: fckmin ≥ 20 MPa
– Dimensões mínimas:
– Medidas mínimas:
a) Para uma estaca:
b) Blocos para 2 estacas
Estacas Ø 25 cm capacidade prevista 18 a 20 T
Ø 30 cm capacidade prevista 25 a 28 T
Obs. Sempre fazer sondagem no terreno, no mínimo três pontos.
As estacas tem 2 tipos de resistência: Atrito lateral e resistência de ponta.
Planta: Corte:

34. d ≥ 50 cm
Ficou adotado que a largura mínima para um bloco de 2 estacas é igual a altura mínima.
O entre eixo será:
Estacas moldadas “in loco” – e = 3 × Ø estaca
Estacas pré fabricadas – e = 2,5 Ø estaca
Ângulo de abertura – ≥ 45º
13/11/2008 14ª aula de Estruturas
Exercícios:
Determinar as dimensões de um bloco que suporta uma carga de 90 T e as estacas serão
pré fabricadas c/ 40 cm de lado, que suporta 50 T cada uma. Determinar a quantidade de estacas
necessárias.
Solução:
a) Quantidade de estacas:
Carga total = 90 T
Capacidade de cada uma das estacas = 50 T
Qde estacas = 90 T ÷ 50 T = 1,8 ≈ 2 estacas
b) Blocos para duas estacas
b1) Corte
Entre eixo = 2,5 × Ø estaca = 2,5 × 40 cm c/ lado = 100 cm
Comprimento do bloco:
CP = (15 + 20 + 100 + 20 + 15) cm = 170 cm

35. h = 50 cm × tg 45º = 50 cm
b2) Planta:
b3) Altura do bloco:
h = ℓ = 50 cm
d = r + h = 50 cm + 5 cm = 55 cm
– Bloco de 4 estacas:
– Bloco de 5 estacas:
Sapatas
– São elementos estruturais de infra–estrutura que transferem as cargas dos pilares
diretamente ao solo.

36. – São dimensionadas em função da taxa de Resistência do Solo (Tipos de Solo).
Tabela Simplificada de Solo
Tipo de Solo
Tensão Admissível
( ) kg/cm² ( ) T/m²
Areia úmida 2 kg/cm² 20 T/m²
Pedregulho e Areia Grossa
5 kg/cm²
a
8 kg/cm²
50 T/m²
a
80 T/m²
Rocha Pura
10 kg/cm²
a
50 kg/cm²
100 T/m²
a
500 T/m²
– Interessa saber a superfície de contato com o solo para que ocorra a distribuição de
cargas.
ASAP =
P
aplicada < adm. do solo
adm. Solo
Exemplo: Qual a área de contato com o solo que deverá ter uma sapata que descarga 80 T
e o solo é arenoso grosso?
a) Calculo da superfície da Sapata:
ASAP = P ÷ SOLO = 80 T ÷ 80 T/m² = 1 m²
b) Superfície adotada:
A*SAP = 1,10 m × 1,10 m = 1,21 m²
c) Verificação da taxa aplicada:
*APLIC = P ÷ A*SAP = 80 T ÷ 1,21 m² = 66,12 T/m² < 80 T/m²
“Podemos executar a sapata”
19/11/2008 15ª aula de Estruturas
Formato das Sapatas
Corte:

37. – Considerações Técnicas
– Concreto: Fckmin: 20 MPa
– Aço CA 50 A
/B Ømin = 10 mm (esp.max = 15 cm) (e≥ 5 cm)
– Restrições e Verificações:
a) h ≥
B – b
+ 5 cm h ≥
A – a
+ 5 cm
4 4
ho ≥ 30 cm (medidas em cm) em casa térrea ho = 15 cm
b) Ângulos:
≥ 30º e ≥ 30º
c) Das restrições acima resulta:
h – ho
≤ 0,288
h – ho
≤ 0,288
A – a B – b
20/11/2008 16ª aula de Estruturas
Lajes
– Conceito elemento estrutural que une as vigas, ajuda na estabilidade estrutural e
receber cargas distribuídas, transferindo–os para as vigas.
Tipos de Lajes

38. a) Lajes maciças – Método de Marcus – Armadas em cruz
– Armadas em uma direção
b) Lajes pré–fabricadas – Convencional
– Treliçada (*)
– Paralela (*)
– Paralela cruzada (*)
– Alveolar
* mais usadas para pequenas obras e de médio porte.
Lajes pré – Fabricadas (treliças)
Tabela de cargas para lajes
a) Para forro q = 50 km/m²
b) Para piso residencial, escritório e enfermarias
Alaje ≤ 12 m² q = 200 kg/m²
Alaje ≥ 12 m² q = 150 kg/m²
c) Piso para reuniões ou de acesso ao publico q = 300 km/m²
d) Laje piso para salão de baile, ginástica ou esportes q = 400 km/m²
e) Lajes destinadas a arquivos, bibliotecas, depósitos
em geral
q = deverá ser calculado para
cada tipo de material
* especificar no projeto qual a finalidade da laje.
Escadas
– Secundários: q = 200 km/m²
– Para edifícios residenciais: q = 250 a 300 km/m²
– Para edifícios públicos: q = 400 a 500 km/m²
Lajes pré – fabricadas
As nervuras sempre deverão ser colocadas no menor sentido da camada. (no sentido do
menor vão).
Exemplo:
Armadura negativa
Ømin = 6,3 mm
O comprimento da armadura negativa se obtem somando o valor de ¼ de cada vão do
cômodo. A mesma deverá estar colocado quando nervuras estiverem de topo uma com a outra.

39. O espaçamento máximo = 20 cm
Normalmente usa–se a malha de 15 cm × 15 cm – Ø 4,2 mm
Não necessita de ferragem negativa
26/11/2008 17ª aula de Estruturas
Detalhes:
Capa ≥ 3 cm
– B Altura da lajota
– H Altura total da laje “crua”
– Concreto pra capa da laje fckmin = 20 MPa (C20)
Obs. Os entre eixos poderão variar entre 30 a 44 cm
– Ømin = para negativos Ø 8,0 mm (CA 50)
– Apoios para lajes pré – fabricadas
a) Termino na viga:

40. b) Passa pela viga:
b1) Passa pela viga com balanço:
c) Paredes sobre laje:
Paredes curtas até 3 metros.
– Beirais

41. 02/12/2008 18ª aula de Estruturas
Reações (Cizalhamentos) Estribos
Momentos fletores (Tração e compressão) Longitudinal.
M = (q×ℓ²) ÷ 8 = (1.800kg × 3m²) ÷ 8 = (1.800 kg × 9 m²) ÷ 8 = 2.025 kg.m = 202,5 T.m
fck = 18 MPa = 180 kg/cm²
Aço: CA 50 A
/B
Seção: 15 × 30 cm
Para converter T.cm
h=
100 cm
1000 T
K2 CA 50
nº * Qde mínimo
nº
2º Passo: Achar o valor de k2 e através da Tabela de fck encontrar o valor de k3 em
relação do tipo do ferro:
Para h = 28 cm
h= k2 √(M ÷ b) 28 = k2 √ (202,5 ÷ 15) 28 = k2 √ 13,5 28 = 3,67 k2
k2 = 28 ÷ 3,67 = 7,63
k2 = 7,5
k3 = 0,36
3º Passo: Calcular a quantidade de ferro necessária para a viga:
Sf = (k3 × M) ÷ h = (0,36 × 202,5) ÷ 28 = 72,90 ÷ 28 = 2,60 cm²
4º Passo: Definir a quantidade de ferro pela a TABELA DE FERROS. (MÃE)
CA 50 A
/B 4 Ø 10 mm
3 Ø 12,5 mm

42. Exemplos 2:
M = (q × ℓ²) ÷ 2 = (800 × (3,20)²) ÷ 2 = 8.192 ÷ 2 = 4.096 = 409,6 T.cm²
fck = 18 MPa = 180 kg/cm²
Aço CA 50 A
/B =
Seção: 35 cm × 15 cm
k2 = 5,5
k3 = 0,41
4º Passo: Achar o valor de k2 e através da Tabela de fck encontrar o valor de k3 em
relação do tipo do ferro:
h = k2 √ (M ÷ b) = 5,5 √(409,6 ÷ 15) = 5,5 × 5,23 = 28,7 cm + 2 cm = 30,7 cm
h = 33 cm
d = 35 cm
3º Passo: Calcular a quantidade de ferro necessária para a viga:
Sf = (k3 ×M) ÷ h = (0,41 × 409,6) ÷ 33 = 5,09 cm²
4º Passo: Definir a quantidade de ferro pela a TABELA DE FERROS. (MÃE)
CA 50 A
/B 5 Ø (1/2”) 12,5 mm