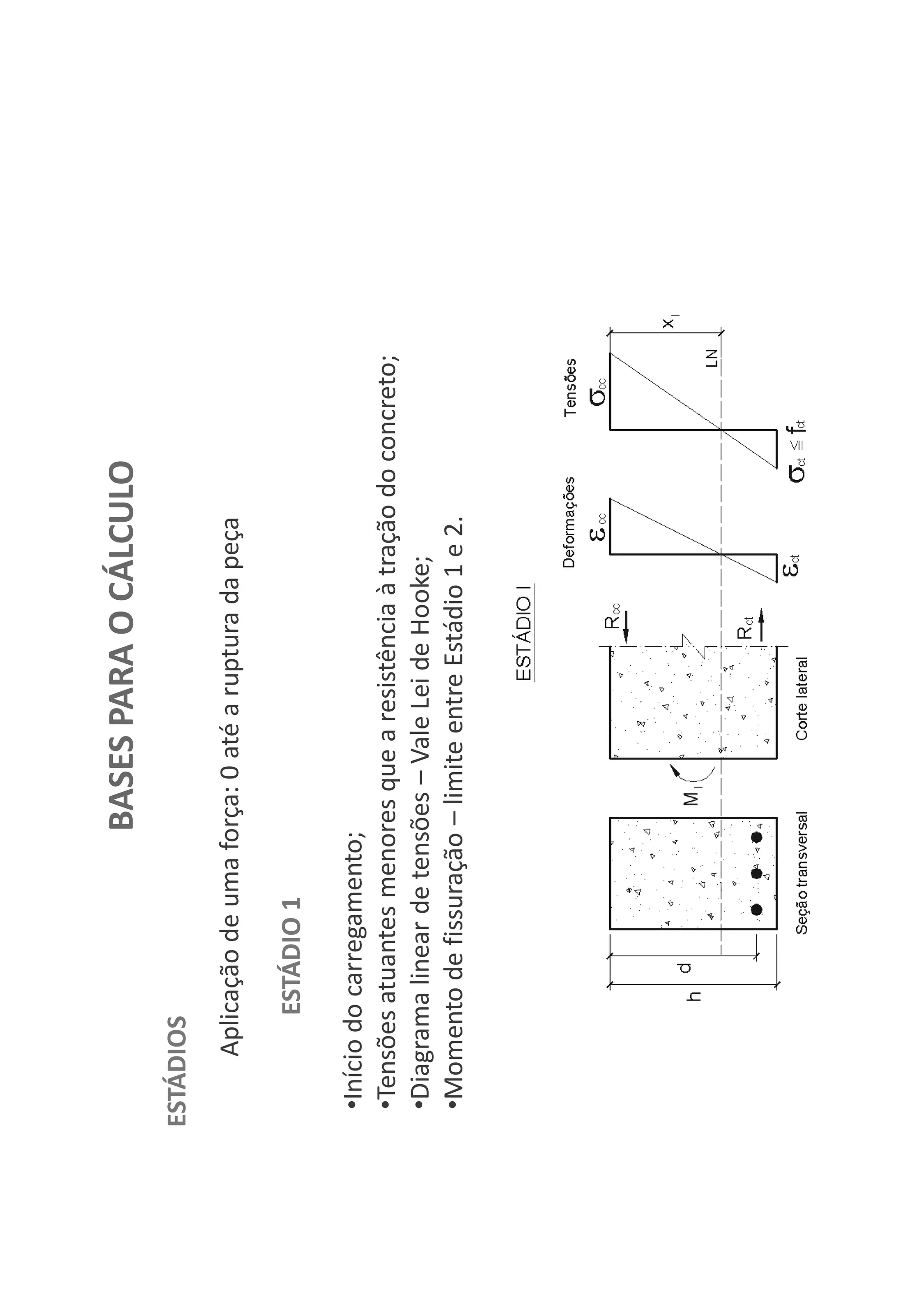
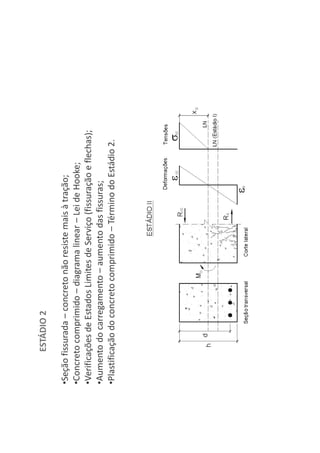
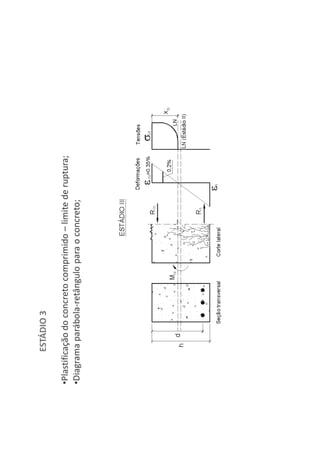
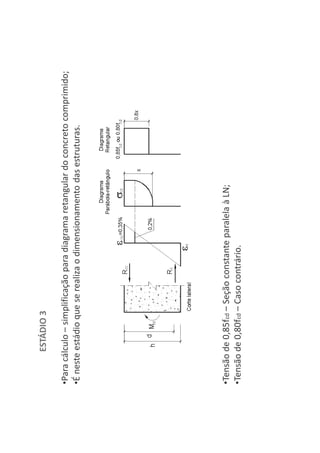
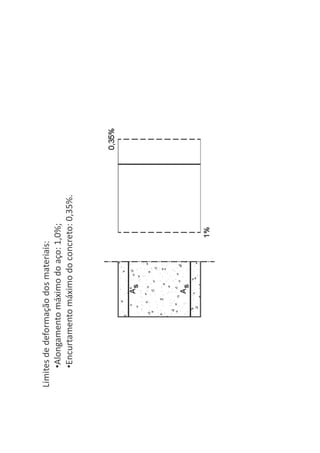
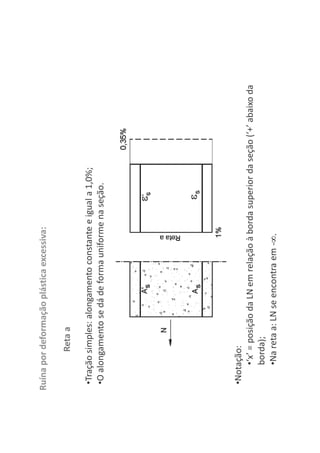
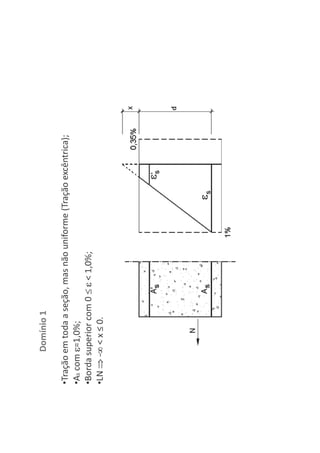
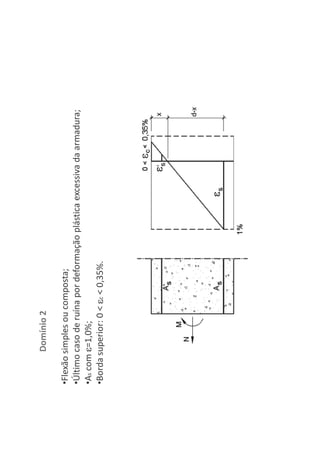
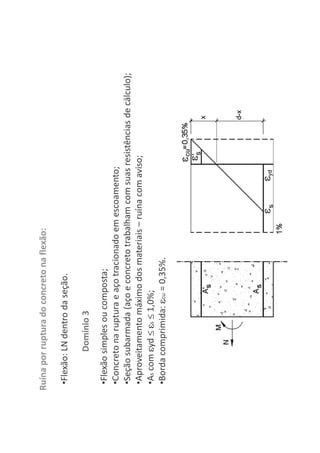
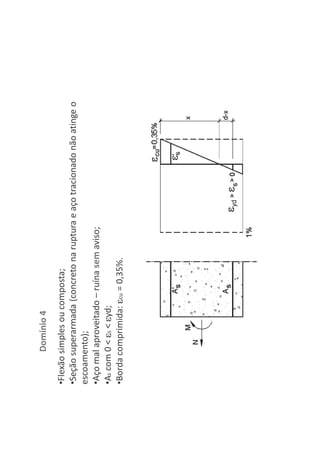
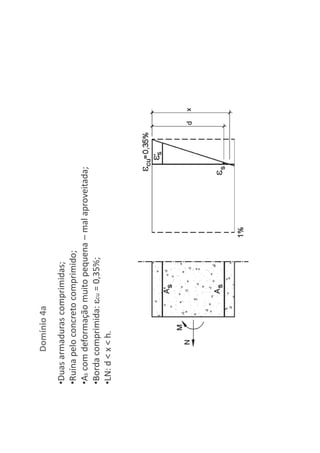
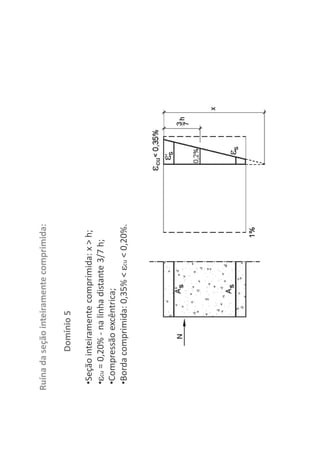
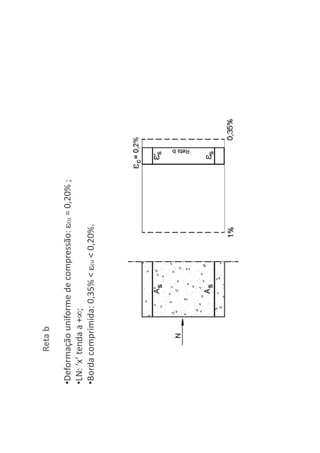
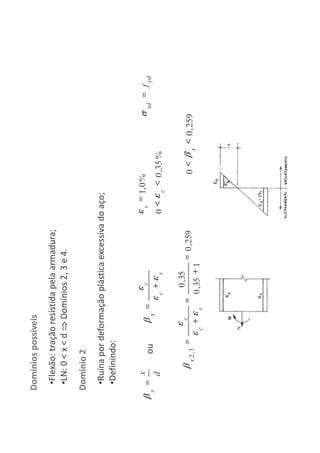
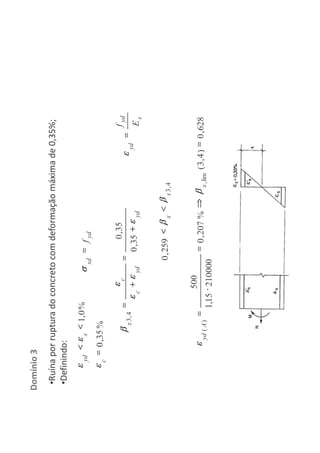
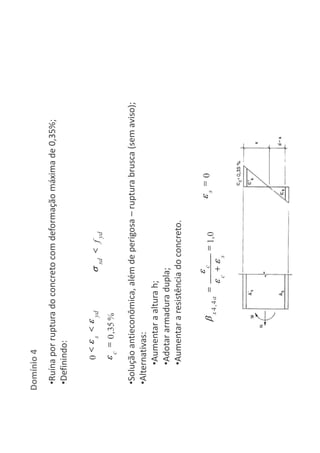
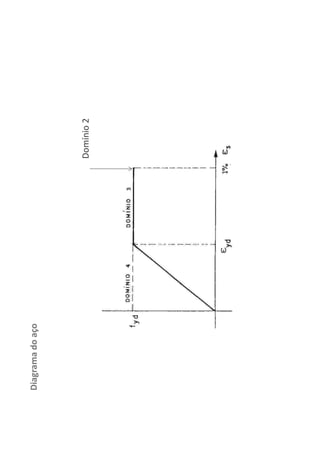
O documento descreve os estágios de cálculo de estruturas de concreto armado sob carga, incluindo os estágios iniciais de carga linear, fissuração do concreto e plastificação, além de definir os domínios de deformação na ruptura considerando os limites dos materiais.

1. BASES PARA O CÁLCULO
Aplicação de uma força: 0 até a ruptura da peça
ESTÁDIOS
ESTÁDIO 1
•Início do carregamento;
•Tensões atuantes menores que a resistência à tração do concreto;
•Diagrama linear de tensões – Vale Lei de Hooke;
•Momento de fissuração – limite entre Estádio 1 e 2.

2. ESTÁDIO 2
•Seção fissurada – concreto não resiste mais à tração;
•Concreto comprimido – diagrama linear – Lei de Hooke;
•Verificações de Estados Limites de Serviço (fissuração e flechas);
•Aumento do carregamento – aumento das fissuras;
•Plastificação do concreto comprimido – Término do Estádio 2.

3. ESTÁDIO 3
•Plastificação do concreto comprimido – limite de ruptura;
•Diagrama parábola-retângulo para o concreto;

4. ESTÁDIO 3
•Para cálculo – simplificação para diagrama retangular do concreto comprimido;
•É neste estádio que se realiza o dimensionamento das estruturas.
•Tensão de 0,85fcd – Seção constante paralela à LN;
•Tensão de 0,80fcd – Caso contrário.

5. •Aço ou concreto atinge o seu limite de deformação:
•Alongamento último do aço (ruína por deformação plástica excessiva do
aço):
•Encurtamento último do concreto (ruína por ruptura do concreto):
Flexão
Compressão simples
DOMÍNIOS DE DEFORMAÇÃO NA RUÍNA
%0,11SUSU
%20,0
%35,0
0
0
CU
CU
CU
CU
Considerações:
•Perfeita aderência entre o aço e o concreto;
•Seções planas permanecem planas.

6. Limites de deformação dos materiais:
•Alongamento máximo do aço: 1,0%;
•Encurtamento máximo do concreto: 0,35%.

7. Ruína por deformação plástica excessiva:
•Tração simples: alongamento constante e igual a 1,0%;
•O alongamento se dá de forma uniforme na seção.
•Notação:
•‘x’ = posição da LN em relação à borda superior da seção (‘+’ abaixo da
borda);
•Na reta a: LN se encontra em - .
Reta a

8. Domínio 1
•Tração em toda a seção, mas não uniforme (Tração excêntrica);
•As com =1,0%;
•Borda superior com 0 < 1,0%;
•LN - < x ≤ 0.

9. Domínio 2
•Flexão simples ou composta;
•Último caso de ruína por deformação plástica excessiva da armadura;
•As com =1,0%;
•Borda superior: 0 < c < 0,35%.

10. Domínio 3
•Flexão simples ou composta;
•Concreto na ruptura e aço tracionado em escoamento;
•Seção subarmada (aço e concreto trabalham com suas resistências de cálculo);
•Aproveitamento máximo dos materiais – ruína com aviso;
•As com yd s 1,0%;
•Borda comprimida: cu = 0,35%.
Ruína por ruptura do concreto na flexão:
•Flexão: LN dentro da seção.

11. Domínio 4
•Flexão simples ou composta;
•Seção superarmada (concreto na ruptura e aço tracionado não atinge o
escoamento);
•Aço mal aproveitado – ruína sem aviso;
•As com 0 < s < yd;
•Borda comprimida: cu = 0,35%.

12. Domínio 4a
•Duas armaduras comprimidas;
•Ruína pelo concreto comprimido;
•As com deformação muito pequena – mal aproveitada;
•Borda comprimida: cu = 0,35%;
•LN: d < x < h.

13. •Seção inteiramente comprimida: x > h;
• cu = 0,20% - na linha distante 3/7 h;
•Compressão excêntrica;
•Borda comprimida: 0,35% < cu < 0,20%.
Domínio 5
Ruína da seção inteiramente comprimida:

14. •Deformação uniforme de compressão: cu = 0,20% ;
•LN: ‘x’ tenda a + ;
•Borda comprimida: 0,35% < cu < 0,20%.
Reta b

15. •LN: definição da posição por semelhança de triângulos.
Diagrama único
•Da reta a para domínios 1 e 2: diagrama gira em torno do ponto A (Armadura
como limite com deformação de 1,0%);
•Nos domínios 3, 4 e 4a: diagrama gira em torno do ponto B (ruptura do concreto
na borda comprimida com deformação de 0,35%);
•Domínios 5 e reta b: diagrama gira em torno do ponto C (Concreto com 0,2%).

16. FLEXÃO SIMPLES NA RUÍNA - EQUAÇÕES
•Momento fletor separado da força cortante;
•Perfeita aderência entre concreto e armadura: c = s;
•Resistência à tração do concreto é desprezada;
•Manutenção da forma plana da seção transversal são proporcionais à
distância em relação à LN
Hipóteses
Diagramas de tensão do concreto

17. •Flexão: tração resistida pela armadura;
•LN: 0 < x < d Domínios 2, 3 e 4.
Domínios possíveis
•Ruína por deformação plástica excessiva do aço;
•Definindo:
Domínio 2
d
x
x
x
x ou
sc
c
x
sc
c
x
%35,00
%0,1
0
1
c
s
c
s ydsd ffsd
259,0
135,0
35,0
3,2 0
1sc
c
x
sc
c
x 259,00 0xx

18. •Ruína por ruptura do concreto com deformação máxima de 0,35%;
•Definindo:
Domínio 3
%35,0
%0,1
0
1
c
syd
c
sy
ydsd ffsd
ydydc
c
x
yyc
c
x
35,0
35,0
4,3
4,3259,0 xx xx
s
yd
yd
E
ff
y
628,0)4,3(%207,0
21000015,1
500
lim,)( 00
2
xAyd xy

19. •Ruína por ruptura do concreto com deformação máxima de 0,35%;
•Definindo:
Domínio 4
%35,0
0
0c
yds
c
ys
ydsd ffsd
•Solução antieconômica, além de perigosa – ruptura brusca (sem aviso);
•Alternativas:
•Aumentar a altura h;
•Adotar armadura dupla;
•Aumentar a resistência do concreto.
0,14,4 1
sc
c
ax
sc
c
x
00ss

20. Diagrama do aço
Domínio 2