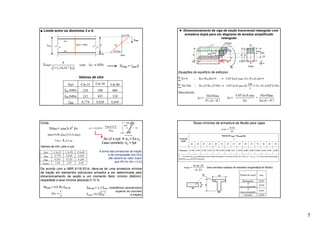
1. O documento discute o dimensionamento de vigas de concreto armado segundo a NBR 6118/2014, incluindo definições de elementos estruturais, diagramas de esforço, etapas de dimensionamento e equações. 2. É detalhado o dimensionamento à flexão simples, com discussão sobre hipóteses, diagramas de tensão-deformação, posição da linha neutra e equações de equilíbrio e compatibilidade. 3. São apresentadas equações para dimensionamento de viga retangular com armadura simples e dupla.

1. 1
Dimensionamento à flexão simples de vigas de concreto
armado segundo a norma NBR 6118/2014
► Generalidades
As edificações são formadas por sistemas estruturais dos mais
diversificados e compostos por diferentes tipos de elementos
estruturais.
Principais elementos estruturais
Piso elementar básico: Laje, vigas e pilares
Modelo real Esquema estático
► Elemento linear – Viga
De acordo com a NBR 6118 (2014), as vigas são elementos
lineares em que a flexão é preponderante.
• Elementos lineares (elementos de barra – eixos)
Relação
adequada
para vigas
• Dimensões
 Largura ou base: bw ≥ 12 cm
 Altura: h ≥ 30 cm (Modulada como múltiplo de 5 cm ou
10cm evitando-se grande variações de altura para vigas
contínuas)
• Vãos efetivos
De acordo com a NBR 6118/2014, o vão efetivo “lef” da viga,
para efeitos de avaliação de esforços, pode ser adotado como:
• Flexão simples: flexão e cisalhamento

2. 2
Diagramas de Momento Fletor e Esforço Cortante
Esquema estático da viga
Reações de apoio
DEC – Diagrama de esforço
cortante
DMF – Diagrama de momento
fletor
A NBR 6118/2014 admite que se dimensione as peças sujeitas à
flexão simples separadamente para os momentos fletores e para
os esforços cortantes.
► Etapas do dimensionamento
 Determinação estática da viga;
 Determinação das ações e cálculo das solicitações;
 Definição dos requisitos dos materiais: concreto e aço;
 Determinação das dimensões da seção transversal;
 Determinação das áreas de aço das armaduras de flexão.
• Ações atuantes
 Peso próprio;
 Alvenarias;
 Lajes;
 Pilares;
 Outras vigas, etc.
Esquema geral de um fluxo de ações
• Coeficientes de ponderação das ações e solicitações (γf)
De acordo com a NBR 6118/2014, as ações características e
consequente solicitações são majoradas para se obter de uma
solicitação de cálculo se dá pela aplicação de um coeficiente de
ponderação sobre as ações que produzem essa solicitação. Para o
estado limite último, tem-se:
Md = γf.Mk
Mk: Momento fletor característico;
Md: Momento fletor de cálculo.
• Coeficientes de ponderação das resistências
De acordo com a NBR 6118/2014, o coeficiente de ponderação
aplicado sobre as resistências dos materiais tem o sentido de
minorar seus valores de referência. Para o estado limite último,
tem-se:
● Resistência de cálculo do concreto (fcd)
Para o concreto com idade igual ou superior a 28 dias, adota-se a
expressão:
Nesse caso, o controle da resistência à compressão do concreto deve ser feito
aos 28 dias, de forma a confirmar o valor de fck (resistência característica à
compressão do concreto) adotado no projeto.

3. 3
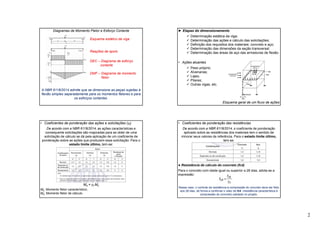
● Resistência de cálculo do aço (fyd)
A resistência de cálculo do aço é obtida a partir de sua resistência
de escoamento característica (fyk), representada pela expressão:
O valor de fyk para os aços sem patamar de escoamento é o valor da tensão
correspondente à deformação permanente de 0,2 %. Para o estado limite
último, pode-se utilizar o diagrama simplificado, para os aços com ou sem
patamar de escoamento.
Diagrama tensão-deformação
para aços de armaduras
passivas
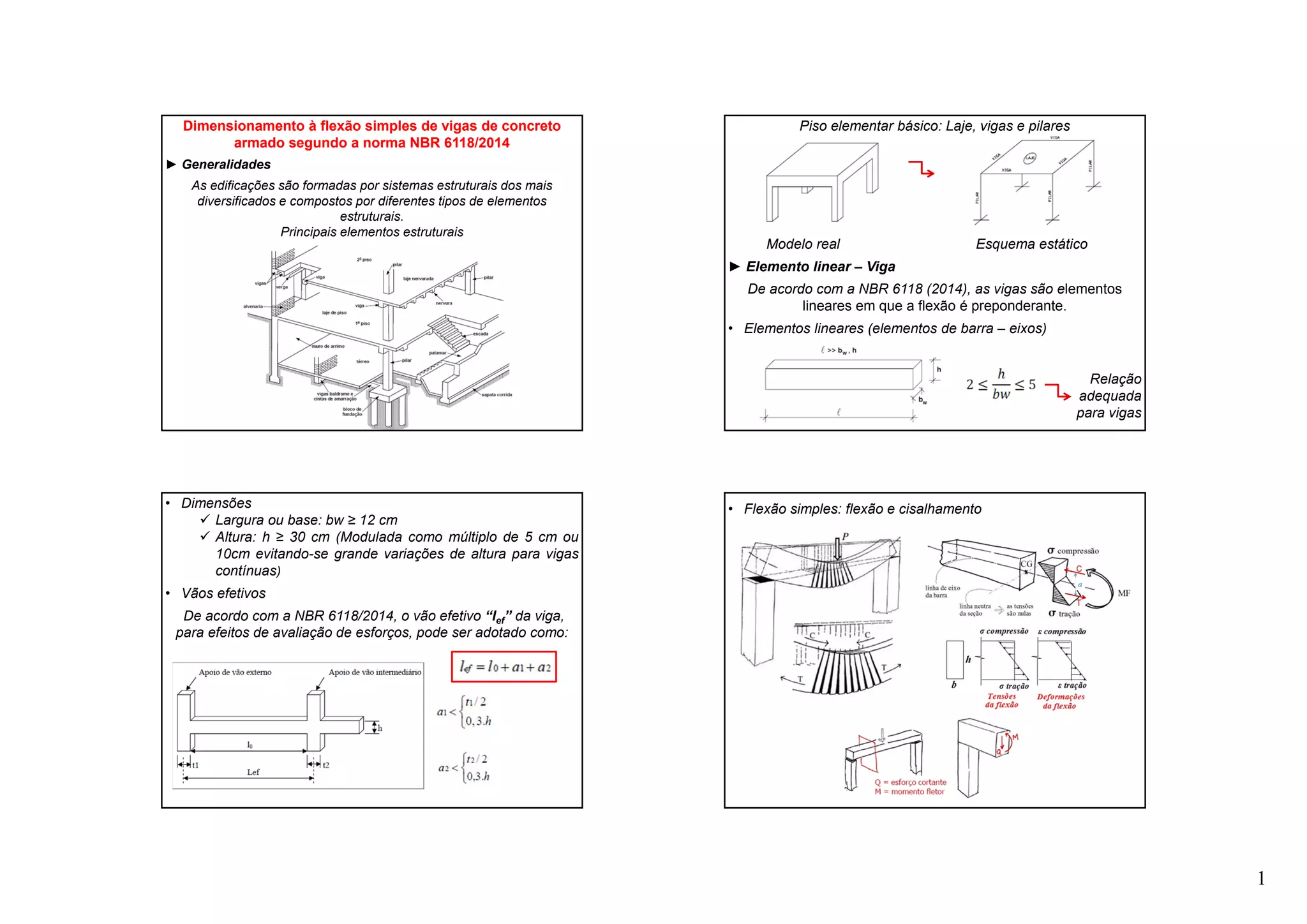
► Dimensionamento à flexão simples “NBR 6118:2014”
A análise de vigas, no estado limite último, é feita com base em
hipóteses básicas, destacando-se:
1) A distribuição de tensões no concreto é feita de acordo com o
diagrama parábola-retângulo, com tensão de pico igual a 0,85 fcd.
εc2: Deformação específica de
encurtamento do concreto no
início do patamar plástico;
εcu: Deformação específica de
encurtamento do concreto na
ruptura.
Diagrama tensão-deformação idealizado
O diagrama tensão-deformação idealizado pode ser substituído pelo
retângulo de profundidade y = λx, com parâmetro λ igual a:
 λ = 0,8, para fck ≤ 50 MPa;
 λ = 0,8 – (fck – 50) / 400, para fck > 50 MPa.
A tensão constante atuante
até a profundidade y
pode ser tomada igual a:
• αc.fcd, no caso da largura
a seção, medida paralelamente
à linha neutra, não diminuir
a partir desta para a
borda comprimida;
• 0,9 αc.fcd, no caso contrário.
Tem-se αc definido como:
• αc = 0,85 para concretos
de classes até C50;
• αc = 0,85 . [1,0 – (fck – 50) / 200]
para concretos de
classes de C50 até C90.
Diagrama tensão-deformação retangular
As diferenças de resultados obtidos com esses dois diagramas são pequenas e
aceitáveis, sem necessidade de coeficiente de correção adicional.
Diagrama tensão-deformação idealizado para retangular
Para proporcionar o adequado comportamento dútil em vigas, a
posição da linha neutra no estado limite último deve obedecer
aos seguintes limites:
a) x/d ≤ 0,45, para concretos com fck ≤ 50 MPa;
b) x/d ≤ 0,35, para concretos com 50 MPa < fck ≤ 90 MPa.

4. 4
2) Caracteriza-se o estado limite último quando a distribuição
de deformações na seção transversal pertencer a um dos seguintes
domínios de deformação:
■ Dependendo do domínio
em que a peça se encontra,
temos a classificação a seguir:
● Seção sub-armada :
Atinge o escoamento na ruptura
(εs > εyd)
● Seção normalmente armada:
Limite entre os domínios 3 e 4.
● Seção super-armada :
Não atinge o escoamento
na ruptura (εs < εyd).
Obs. Para a análise
do diagrama, considere:
- Os pontos (A),
(B) e (C) são chamados
de pólos de ruína.
- As é a armadura
mais tracionada.
- A’s é a armadura
menos tracionada, ou comprimida.
► Dimensionamento de viga de seção transversal retangular com
armadura simples para um diagrama de tensões simplificado
retangular
Equações de equilíbrio de esforços:
Resultando:
► Equações de compatibilidade de deformação
■ As equações de compatibilidade de deformação descrevem as
posições possíveis de uma seção transversal após a deformação
do elemento estrutural, permitindo assim, associar à seção
transversal um estado de tensões conhecido, com base nas
equações constitutivas dos materiais (σ x ε).
■ A partir das hipóteses adotadas e do diagrama dos domínios de
deformação, é possível estabelecer o valor da profundidade da
linha neutra “x”, nas vizinhanças entre dois domínios.
■ Limite entre os domínios 1 e 2:
■ Limite entre os domínios 2a e 2b:
■ Limite entre os domínios 2 e 3:

5. 5
■ Limite entre os domínios 3 e 4:
Valores de εlim
► Dimensionamento de viga de seção transversal retangular com
armadura dupla para um diagrama de tensões simplificado
retangular
Equações de equilíbrio de esforços:
Resultando:
Onde:
Se ε2 ≤ εyd  σ2 = Es.ε2
Caso contrário: σ2 = fyd
Valores de εlim, μlim e εyd
A soma das armaduras de tração
e de compressão (As+A’s)
não deverá ter valor maior
que 4%.Ac (Ac = b.h)
De acordo com a NBR 6118:2014, deve-se ter uma armadura mínima
de tração em elementos estruturais armados a ser determinada pelo
dimensionamento da seção a um momento fletor mínimo (Mdmin),
respeitada a taxa mínima absoluta 0,15 %.
(resistência característica
superior do concreto
à tração)
Taxas mínimas de armadura de flexão para vigas

6. 6
► Espaçamentos entre as barras
■ O arranjo das armaduras deve atender não só à sua função
estrutural, como também às condições adequadas de execução,
particularmente com relação ao lançamento e ao adensamento
do concreto.
■ O espaçamento mínimo livre entre as faces das barras
longitudinais, medida no plano da seção transversal, deve ser
igual ou superior ao maior dos seguintes valores:
Onde:
● A  Espaço para vibrador: 35/50/75/100 mm.
● c  Cobrimento de concreto.
● φi Diâmetro da barra de flexão.
● Espaçamentos horizontal (eh)
● Espaçamentos vertical (ev)
Obs: Os valores de espaçamentos horizontais e veticais se
aplicam também nas regiões com emendas por traspasse das
barras.
► Resultante nas armaduras de flexão
■ O esforço resultante nas armaduras de tração ou de
compressão, poderá ser considerado aplicado no centro de
gravidade das respectivas armaduras, somente se a distância (h’)
entre esse ponto ao ponto da seção da armadura mais afastado
da LN, medido perpendicularmente à mesma, não ultrapassar
10% da altura (h) da viga. Caso contrário, a resultante deverá ser
desmembrada em igual número de camadas existentes, e novas
equações de equilíbrio deverão ser obtidas.
Consideração da resultante de tração nas armaduras
► Armadura de pele
■ A armadura de pele tem por função controlar a abertura de
fissuras nas regiões tracionadas das vigas. Em vigas com altura
menores ou iguais a 60cm a armadura de pele pode ser
dispensada.
■ A armadura de pele é calculada por:
■ O espaçamento da armadura de pele é dada por:
20 cm
e ≤