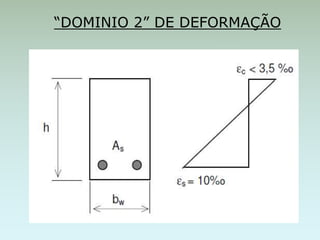
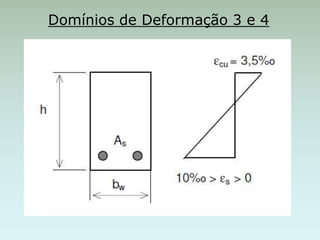
O documento discute os domínios de deformação em estruturas de concreto armado sujeitas à flexão. São definidos quatro domínios de acordo com os limites de deformação do concreto e da armadura. Exemplos numéricos ilustram o cálculo da altura útil e da área de aço necessária para resistir a momentos fletores em diferentes configurações.