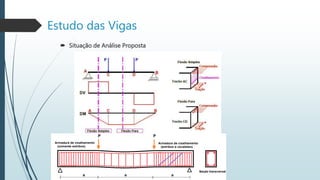
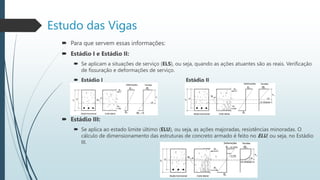
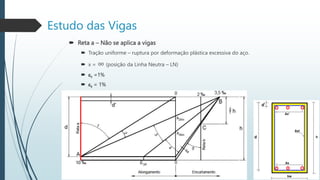
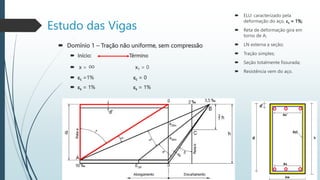
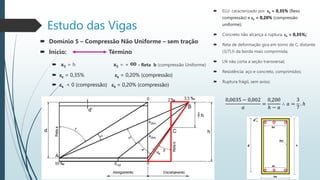
O documento descreve os estágios de deformação de uma viga de concreto armado sob carga crescente, incluindo: - Estádio I - estado elástico sem fissuras visíveis; - Estádio II - estado de fissuração com fissuras visíveis; - Estádio III - estado próximo à ruína com muitas fissuras profundas. Também define os domínios de deformação no estado limite último, caracterizados pelas deformações do concreto e do aço.

1. Estudo das Vigas
 Beto Borja
 Marcio Varela
Estádios - Estados de Fissuração

2.  Processo de Colapso de Uma Viga
 Admitindo-se uma viga de concreto armado sujeita a um carregamento crescente e que, este
cause uma flexão pura (V = 0 e M = constante) na região central da viga, tem-se os seguintes
níveis de deformações da viga em estudo, conhecidos como:
 ESTÁDIO I;
 ESTÁDIO II; e
 ESTÁDIO III;
 Considerações:
 O momento varia de 0 (zero) até um valor que promova o colapso de estrutura;
 Admite-se que a seção transversal da viga permaneça plana durante todo o processo.
Estudo das Vigas

3.  Situação de Análise Proposta
Estudo das Vigas

4.  ESTÁDIO I – Estado Elástico
 Sob a ação do momento fletor MI, de pequena intensidade, a tensão de tração no
concreto não ultrapassa sua resistência característica à tração (ftk):
 Diagramam de tensão normal ao longo da seção é linear;
 As tensões nas fibras mais comprimidas são proporcionais às deformações,
correspondendo ao trecho linear do diagrama tensão-deformação do concreto;
 Não há fissuras visíveis.
Estudo das Vigas

5.  ESTÁDIO II – Estado de Fissuração
 Aumentando o valor do momento fletor para MII, as tensões de tração na maioria dos
pontos abaixo da linha neutra (LN) terão valores superiores ao da resistência
característica à tração do concreto (ftk):
 Considera-se que somente o aço resiste aos esforços de tração;
 Admite-se que a tensão de compressão no concreto continue linear;
 As fissuras de tração na flexão no concreto são visíveis.
Estudo das Vigas

6.  ESTÁDIO III – Estado de Fissuração
 Aumentando o valor do momento fletor para MIII (MU), próximo da ruina, e, considerando
considerando os concretos até C50:
 A fibra mais comprimida do concreto começa a plastificar a partir da deformação
específica de ec2 = 0,2%, chegando a atingir, sem aumento de tensões a deformação
específica ecu = 0,35%;
 O diagrama de tensões tende a ficar vertical (uniforme), com quase todas as fibras
trabalhando com sua tensão máxima, ou seja, praticamente todas as fibras atingiram
deformações superiores a ec2 = 0,2%, e chegando até ecu = 0,35%;
Estudo das Vigas

7.  ESTÁDIO III – Estado de Fissuração
 A peça estará muito fissurada, com fissuras profundas, fazendo com que a altura da
região comprimida seja diminuída;
 Supõe-se que a distribuição de tensões no concreto ocorra segundo um diagrama
parábola retângulo;
Estudo das Vigas

8.  Para que servem essas informações:
 Estádio I e Estádio II:
 Se aplicam a situações de serviço (ELS), ou seja, quando as ações atuantes são as reais. Verificação
de fissuração e deformações de serviço.
 Estádio I Estádio II
 Estádio III:
 Se aplica ao estado limite último (ELU), ou seja, as ações majoradas, resistências minoradas. O
cálculo de dimensionamento das estruturas de concreto armado é feito no ELU, ou seja, no Estádio
III.
Estudo das Vigas

9. Estudo das Vigas
Domínios de Deformação

10.  Hipóteses Básicas de Cálculo no ELU – NBR 6118:2014 – ITEM 17.2.2
 As seções transversais se mantêm planas após a deformação;
 A deformação específica das barras, em tração ou compressão, deve ser a mesma do concreto em
seu entorno;
 As tensões de tração no concreto, normais à seção transversal, podem ser desprezadas,
obrigatoriamente no ELU;
 A ruina da seção transversal para qualquer tipo de flexão no estado limite último fica caracterizada
pelas deformações específicas do concreto (ec) e do aço (es), quando atingem seus valores últimos
(uma delas ou ambos);
Estudo das Vigas

11. Estudo das Vigas
 Hipóteses Básicas de Cálculo no ELU
 Encurtamentos últimos do concreto no ELU:
 Para concretos de classe até C50:
 ec2 = 0,20% - Ocorre nas seções totalmente comprimidas;
 ecu = 0,35% - Ocorre nas seções sob flexão;
 Alongamento último da armadura:
 es = 1% - para prevenir deformação plástica excessiva.

12. Estudo das Vigas
 Hipóteses Básicas de Cálculo no ELU
 Para concretos até a classe C50 a distribuição de tensão no concreto se faz de acordo com um diagrama curvo e retangular,
esse diagrama, segundo item 17.2.2 da norma, pode ser substituído por um retângulo de profundidade y = 0,8.X, onde a
distribuição de tensão é uniforme.
 0,85.fcd no caso da largura da seção, medida paralelamente à linha neutra, não diminuir a partir desta para a borda
comprimida;
 0,80.fcd no caso da largura da seção, medida paralelamente à linha neutra, diminuir a partir desta para a borda comprimida;

13. Estudo das Vigas
 Hipóteses Básicas de Cálculo no ELU
 A tensão nas armaduras deve ser obtida a partir dos diagramas tensão-deformação do aço;
 O estado limite último é caracterizado quando a distribuição das deformações na seção transversal pertencer a
um dos domínios da flexão, definidos a seguir.
 DOMÍNIOS DAS DEFORMAÇÕES DO ELU: concreto classe < C50

14.  Reta a – Não se aplica a vigas
 Tração uniforme – ruptura por deformação plástica excessiva do aço.
 x = ∞ (posição da Linha Neutra – LN)
 ec =1%
 es = 1%
Estudo das Vigas

15.  Domínio 1 – Tração não uniforme, sem compressão
 Início: Término
 x = ∞ x1 = 0
 ec =1% ec = 0
 es = 1% es = 1%
Estudo das Vigas
 ELU: caracterizado pela
deformação do aço, es = 1%;
 Reta de deformação gira em
torno de A;
 LN externa a seção;
 Tração simples;
 Seção totalmente fissurada;
 Resistência vem do aço.

16. Estudo das Vigas
 ELU: caracterizado pela
deformação do aço, es = 1%;
 Concreto não alcança a ruptura, ec
< 0,35%;;
 Reta de deformação gira em torno
de A;
 LN corta a seção transversal;
 Resistência: aço e concreto;
 Domínio 2 – Flexão Simples ou Composta
 Início: Término
 x1 = 0 x2 = 0,259.d
 ec = 0 ec = 0,35%
 es = 1% es = 1%
0,0035
𝑥2
=
0,01
𝑑 − 𝑥2
∴ 𝑥2 = 0,259. 𝑑

17. Estudo das Vigas
 ELU: caracterizado pela deformação e
ruptura do concreto, ec = 0,35%;
 Reta de deformação gira em torno de B;
 LN corta a seção transversal, entre os limites
3 e 4;
 Resistência: aço e concreto, ruptura e
escoamento simultâneos;
 Domínio ideal de cálculo.
 Domínio 3 – Flexão Simples (subarmada) ou Composta
 Início: Término
 x2 = 0,259.d x3 = varia com o tipo de aço
 ec = 0,35% ec = 0,35%
 es = 1% es = eyd - deformação específica do aço
 eyd CA50 = 0,207% 0,0035
𝑥3
=
𝜀𝑦𝑑
𝑑 − 𝑥3
∴ 𝑥3 =
0,0035. 𝑑
𝜀𝑦𝑑 + 0,0035

18. Estudo das Vigas
 Domínio ideal de cálculo (NBR-
6118/2014).
 Anterior:
 Nova Condição de cálculo:
 Domínio 3 – Flexão Simples (subarmada) ou Composta
 Parte desse Domínio não pode ser mais usado em função do
limite x/d imposto pela NBR 6118:2014. A justificativa é garantir
as condições mínimas de ductilidade.
0,259. 𝑑 < 𝑥 ≤
0,0035. 𝑑
𝜀𝑦𝑑 + 0,0035
𝑥34 ≤ 0,628.d
𝑥
𝑑
≤ 0,45 para fck ≤ 50MPa. Mais
restritivo que 𝒙𝟑𝟒;
𝑥
𝑑
≤ 0,35 para 50 Mpa < fck ≤ 90 MPa;
𝑥
𝑑
≤ 0,45

19. Estudo das Vigas
 ELU: caracterizado pela deformação e ruptura
do concreto, ec = 0,35%;
 Reta de deformação gira em torno de B;
 LN corta a seção transversal, tração e
compressão;
 Deformação da armadura inferior a eyd;
 Resistência: aço e concreto, ruptura frágil;
 Peças super armadas
 Domínio 4 – Flexão Simples (super armada) ou Composta
 Início: Término
 x3 = x3
* x4 = d
 ec = 0,35% ec = 0,35%
 es = eyd es = 0

20. Estudo das Vigas
 ELU: caracterizado pela deformação e ruptura
do concreto, ec = 0,35%
 Reta de deformação gira em torno de B;
 LN corta a seção transversal no cobrimento
menos comprimido;
 Resistência: aço e concreto, comprimidos;
 Ruptura frágil, sem aviso;
 Pequena zona de concreto tracionado.
 Domínio 4a – Flexão Composta com armadura Comprimida
 Início: Término
 x4a = d x4a = h
 ec = 0,35% ec = 0,35%
 es = 0 es < 0 (compressão)

21. Estudo das Vigas
 ELU: caracterizado por ec = 0,35% (flexo
compressão) e ec = 0,20% (compressão
uniforme);
 Concreto não alcança a ruptura, ec < 0,35%;;
 Reta de deformação gira em torno de C, distante
(3/7).h da borda mais comprimida;
 LN não corta a seção transversal;
 Resistência: aço e concreto, comprimidos;
 Ruptura frágil, sem aviso;
 Domínio 5 – Compressão Não Uniforme – sem tração
 Início: Término
 x5 = h x5 = + ∞ - Reta b (compressão Uniforme)
 ec = 0,35% ec = 0,20% (compressão)
 es < 0 (compressão) es = 0,20% (compressão)
0,0035 − 0,002
𝑎
=
0,200
ℎ − 𝑎
∴ 𝑎 =
3
7
. ℎ

22. Equações de Compatibilidade de Deformação
Próxima Aula
Estudo das Vigas
 Beto Borja
 Marcio Varela