Elepot2006 proj (1)

Eletrônica de Potência
Fevereiro/2006Prof. Ricardo Ribeiro 1
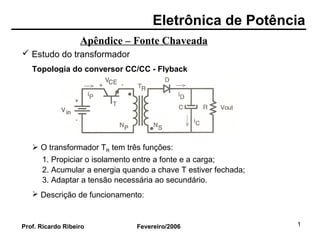
Apêndice – Fonte Chaveada
 Estudo do transformador
Topologia do conversor CC/CC - Flyback
 O transformador TR tem três funções:
1. Propiciar o isolamento entre a fonte e a carga;
2. Acumular a energia quando a chave T estiver fechada;
3. Adaptar a tensão necessária ao secundário.
 Descrição de funcionamento:

 Estudo do transformador
Cálculo do núcleo do transformador para a fonte Flyback
Seja a lei de Faraday:
dt
dB
ANV epin =
onde: Np é o número de espiras do primário, Ae é a área da secção
transversal do núcleo e B é a densidade de fluxo magnético.
A derivada dB/dt pode ser aproximada por:
ont
B
t
B
dt
dB ∆
=
∆
∆
=
Conseqüentemente,
D
BfAN
t
BAN
V
sep
on
ep
in
∆
=
∆
= com
s
on
T
t
D =

Desse modo:
 Estudo do transformador: cálculo do núcleo
sp
in
e
BfN
VD
A
∆
= max
Considere o núcleo com o formato da Fig. abaixo,
Em que:
Ap – área ocupada pelo primário.
Kw – fator de utilização da área do
enrolamento.
Aw – área da janela do núcleo.
Kp – fator de utilização do primário.
Assim:
wwpp AKKA =

Considere a relação:
JAIN ppefp =
onde J é a densidade de corrente no condutor e ipef é o valor eficaz da
corrente no primário.
Então,
wwp
pefp
p AKK
J
IN
A == ou
JKK
IN
A
wp
pefp
w =
Manipulando-se as equações anteriores, pode-se escrever:
swp
pefin
we
wp
pefp
sp
in
we
BfJKK
IVD
AA
JKK
IN
BfN
VD
AA
∆
=⇒
∆
=
maxmax
Para o conversor flyback,
3
(max)
D
II ppef = mas
D
I
I
medp
p
)(
(max)
2
= assim,
D
II medppef
3
4
)(=

onde η é o rendimento da fonte (η = 0.7 - pior caso), Pout é a potência de
saída e Pin é a potência de entrada.
Consequentemente,
Desta forma,
D
BfJKK
IV
AA
swp
medpin
we
3
4)(
∆
=
Seja Dmax = 0.45 (valor de projeto), então:
swp
medpin
we
BfJKK
IV
AA
∆
=
)(77,0
Por outro lado,
η
out
medpinin
P
IVP == )(
swp
out
we
BfJKK
P
AA
∆
=
1.1

Considere as seguintes unidades:
Pout[W] – potência de saída;
J[A/cm2
] – densidade de corrente;
fs[Hz] – freqüência de chaveamento;
∆B[T] – variação de fluxo magnético;
Assim:
4
4
101.1
cm
BfJKK
P
AA
swp
out
we
∆
=
 Estudo do transformador: escolha dos condutores
A área da seção reta do condutor é dado por:
J
I
S pef
cm =

 Estudo do transformador: exemplo numérico
Especificar o núcleo de uma fonte flyback em condução descontínua para:
Pout = 60W, fs = 67kHz, Kp = 0.5, Kw = 0.4, J = 200A/cm2
e ∆B = 0.16T
Solução: 4
4
101.1
cm
BfJKK
P
AA
swp
out
we
∆
=
4
3
4
54.1
16.010672004.05.0
10601.1
cmAA we =
×××××
××
=
A partir da tabela de núcleos EE, escolhe-se o núcleo E 42/15.
 Estudo do transformador: cálculo do entreferro
A energia armazenada no indutor, no instante ton, é:
BHVILW pp
2
1
2
1 2
(max) ⇒=∆
onde V é o volume do entreferro.

Como:
V
B
W
B
H
0
2
0 2
1
µµ
=∆⇒=
em que, sendo δ o comprimento do entreferro. Então:δeAV =
e
e
AB
W
A
B
W 2
0
0
2
2
2
1 ∆
=⇒=∆
µ
δδ
µ
2/δ=gl
Núcleo de Ferrite - EE
A energia ∆W pode ser obtida como segue:
s
out
in Wf
P
P ∆==
η
Assim,
s
out
f
P
W
η
=∆

Condições de contorno para potência de saída
 A densidade de fluxo de saturação para o ferrite é da ordem de 0.3T.
 O ciclo de trabalho, inferior a Bmax, depende de fs.
 Quando fs aumenta, o valor de B deve diminuir para reduzir perdas.
 Deve-se garantir que quando Vin aumenta, D <= Dmax.
As restrições acima, podem ser descritas como segue:
sppoutpp
s
out
fILPIL
f
P
η
η
2
(max)
2
(max)
2
1
2
1
=⇒=
Por outro lado,
(max)
(max)
(max)
(max)
(max)
(max)
min
D
fIL
TD
IL
t
IL
V
spp
s
pp
on
pp
===
Assim,
(max)min(max)
(max)
(max)min2
(max)
(max)
(max)min
2
1
2
1
DVI
fI
DV
fIP
fI
DV
L p
p
spout
sp
p ηη ==⇒=

Conseqüentemente, a corrente do primário pode ser dada por:
(max)min
(max)
2
DV
P
I out
p
η
=
Para η = 0.7 e Dmax = 0.45,
min
(max)
35.6
V
P
I out
p =
Exemplo numérico: seja uma fonte com as seguintes características;
Pout = 60W, fs = 67kHz, Vmin = 36V, Vmax = 76V, η = 0.7
Solução:
A
V
P
I out
p 6.10
36
6035.635.6
min
(max) =
×
==
J
f
P
W
s
out 3
3
1028.1
10677.0
60 −
×=
××
==∆
η

Exemplo numérico: continuação da solução
mm
AB
W
e
69.0
1018116.0
1028.110422
62
37
2
0
=
××
××××
=
∆
= −
−−
πµ
δ
mmlg 345.0
2
==
δ
 Estudo do transformador: enrolamento primário
Seja a relação:
(max)
(max)
4.0
4.0
p
ppp
I
B
NBIN
π
δ
δπ =⇒=
28.8
6.104.0
069.01600
=
×
×
=
π
pN • B (gauss) e δ (cm)
Com os dados do exemplo anterior,

 Estudo do transformador: enrolamento secundário
A tensão do enrolamento secundário é dado por:
douts VVV +=
onde Vd é a tensão sobre o diodo retificador.
Para que a desmagnetização seja assegurado:
φ∆== onpoffs
s
p
tVtV
N
N
Seja o pior caso dado por:
(max)(max)(max) )( onponss
s
p
onsoff tVtTV
N
N
tTt =−⇒−=
Assim,
(max)
(max)
(max)(max)
)1(
)1(
D
D
V
V
NNDVDV
N
N
p
s
psps
s
p −
=⇒=−
(max)
(max) )1()(
D
D
V
VV
NN
p
dout
ps
−+
=

 Estudo do transformador: enrolamento secundário
Seja: Vout = 12V, Vd = 1V e Dmax = 0.45, então:
64.3
45.036
)45.01)(112(
28.8
)1()(
(max)
(max)
=
×
−+
=
−+
=
D
D
V
VV
NN
p
dout
ps
Enrolamento secundário pra múltiplas saídas:
Para cada saída, é empregada uma expressão como segue:
(max)
(max)
(min)
)( )1()(
D
D
V
VV
NN
p
dnout
psn
−+
=
Sendo n um enrolamento qualquer secundário.

Elepot2006 proj (1)

Mais conteúdo relacionado

Mais procurados

Semelhante a Elepot2006 proj (1)

Mais de JADSON SANTOS

Último

Elepot2006 proj (1)