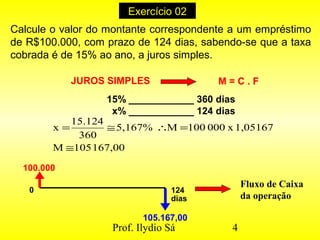
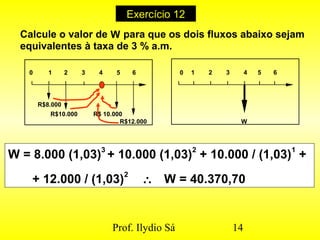
1) O documento apresenta exercícios resolvidos de matemática financeira, incluindo cálculos de juros simples e compostos, taxas nominais e efetivas. 2) São mostrados exemplos como calcular o aumento acumulado de preços com inflação, taxas de juros anuais e períodos menores, e determinar valores futuros ou tempos de aplicação financeira. 3) Os exercícios visam aplicar conceitos como juros, descontos, equivalentes e fluxos de caixa em situações financeiras.

1. MATEMÁTICA FINANCEIRA
NA EDUCAÇÃO BÁSICA
EXERCÍCIOS GERAIS
RESOLVIDOS
PROF. ILYDIO PEREIRA DE SÁ

2. Prof. Ilydio Sá 2

3. Prof. Ilydio Sá 3
Exercício 01
Uma mercadoria sofreu 4 acréscimos consecutivos de 3%, 4%, 6,5%
e 8%, respectivamente. Nesse mesmo período, as taxas de inflação
correspondente foram de 2%; 1,5%; 5% e 3%. Obtenha:
a) A taxa nominal correspondente ao aumento total acumulado
dessa mercadoria.
b) A taxa de inflação acumulada do período.
c) A taxa real de aumento dessa mercadoria.
a) 1,03 x 1,04 x 1,065 x 1,08 ≅ 1,2321 - fator de aumento da
mercadoria, logo, (1,2321 – 1) x 100 ≅ 23,21% é a taxa nominal do
aumento acumulado da mercadoria.
b) 1,02 x 1,015 x 1,05 x 1,03 ≅ 1,1197 – fator de inflação
acumulada, logo, (1,1197 – 1) x 100 ≅ 11,97% é a taxa de inflação
acumulada.
c) Fator de aumento real = 1,1004
1197,1
2321,1
≅
Taxa real de aumento da mercadoria (1,1004 – 1) x 100 ≅ 10,04%

4. Prof. Ilydio Sá 4
Exercício 02
15% ____________ 360 dias
x% ____________ 124 dias
JUROS SIMPLES M = C . F
105.167,00
100.000
0 124
dias
Calcule o valor do montante correspondente a um empréstimo
de R$100.000, com prazo de 124 dias, sabendo-se que a taxa
cobrada é de 15% ao ano, a juros simples.
167,00105M
1,05167x000100M5,167%
360
15.124
x
≅
=∴≅=
Fluxo de Caixa
da operação

5. Prof. Ilydio Sá 5
Um capital de R$50.000, aplicado durante 10 meses, rende
juros de R$8.000. Determinar a taxa anual correspondente,
se a aplicação foi a juros simples.
58.000
50.000
0 10
Exercício 03
JUROS SIMPLES M = C . F
meses10para%,16detaxa1,16
00050
00058
F ⇒==
19,2%12x1,6%anualtaxa%6,1
10
16%
imensal,taxa ==∴==

6. Prof. Ilydio Sá 6
JUROS SIMPLES
13.000
10.000
0 12
Exercício 04
Taxa global da operação = 2,5% x 12 = 30%, logo fator = 1,3
Calcular o montante da aplicação de um
capital de R$ 10.000 pelo prazo de 12 meses, à
taxa de 2,5 % a.m., a juros simples.
M = 10 000 x 1,3 = 13 000,00
Fácil, não ?

7. Prof. Ilydio Sá 7
Calcular o montante de um capital de R$ 100.000,
aplicado à taxa de 4,5 % a.m., durante 11 meses.
M = C . F
n
i = 4,5% a.m.
M
100.000
0 11
Exercício 05
M = 100.000 . (1,045)
11
=
M = 162.285,30

8. Prof. Ilydio Sá 8
i = ?
25.600
20.000
0 6
M = C . F
n
Exercício 06
Qual a taxa aproximada, de uma aplicação que rendeu o
montante de R$ 25 600, a partir de um investimento de R$ 20 000,
por um prazo de 6 meses?
mês.ao4,2%deéaproximadataxaaLogo,
1,0421,28F1,28F
28,1
00020
60025
F
66
6
≅=∴=
==

9. Prof. Ilydio Sá 9
Que quantia deve ser investida, hoje, a fim de acumular
R$ 200.000, em 10 anos, à taxa de 10 % a.a. ?
i = 10 % a.a.
200.000
C
0 10
M = C . F
n
Exercício 07
C = 200.000 / 1,1
10
=
C = 77.108,66

10. Prof. Ilydio Sá 10
Exercício 08
i = 8 % a.a.
12.000
5.000
0 n
log(1,08)
log(2,4)
n(2,4)log(1,08)log.n
2,41,08
2,4
5000
00012
1,08
000121,08x5000
n
n
n
=∴=
=
==
=
0,380211-0,477120,30103.3
10log-3log2log.3
10log-3)x(2log
10
24
log(2,4)log 3
≅+≅
≅+=
==
0,033422-3.0,477120,30103.2
100log-33.log2log.2
100log-)3x(2log
100
108
log(1,08)log 32
≅+≅
+=
==
anos11,3767
0,03342
0,38021
log(1,08)
(2,4)log
n ≅≅=
Por quanto tempo deve ser colocado o capital de R$ 5.000, à taxa de
8% a.a, a fim de produzir um montante de R$ 12 000, sendo a
capitalização anual. Dados: log 2 ≅ 0,30103 e log 3 ≅ 0,47712

11. Prof. Ilydio Sá 11
Exercício 09
Imagine uma caderneta de poupança hipotética
que ofereça juros de 4,5% ao semestre, com
capitalização bimestral dos juros. Determine a
taxa de juros semestral efetiva.
4,5% ao semestre, com juros bimestrais = TAXA NOMINAL
Como 1 semestre possui 3 bimestres:
TAXA EFETIVA BIMESTRAL = 4,5% a.s. / 3 = 1,5% a.b.
Capitalizando-se 1,5% a.b. a juros compostos, durante
3 bimestres, pelo Fator (1 + i)n
:
TAXA SEMESTRAL EFETIVA = (1,015)3
= 1,0457
4,57% a.s.

12. Prof. Ilydio Sá 12
A taxa de juros de um empréstimo bancário é de
14% a.a., com pagamento trimestral dos juros.
Determine a taxa efetiva anual do empréstimo.
Exercício 10
14% a. a., com pgto trimestral de juros = TAXA NOMINAL
Como 1 ano possui 4 trimestres:
TAXA EFETIVA TRIMESTRAL = 14% a.a. / 4 = 3,5% a.t.
Capitalizando-se 3,5% a.t. a juros compostos, durante 4
trimestres, pelo Fator (1 + i)n
:
TAXA EFETIVA ANUAL = (1,035)4
= 1,1475 → 14,75% a.a.

13. Prof. Ilydio Sá 13
Exercício 11
Um financiamento foi combinado sob taxa de 15% ao
ano, com capitalização anual. Qual a taxa equivalente,
para uma base de juro quadrimestral?
1 ano = 3 quadrimestres
qF qF qF
aF
%.4,77deépedida
ralquadrimesttaxaaLogo,
1,047715,1F
1,15FFF
3
q
3
qa
3
q
≅=
=⇒=

14. Prof. Ilydio Sá 14
Calcule o valor de W para que os dois fluxos abaixo sejam
equivalentes à taxa de 3 % a.m.
R$12.000
0 1 2 3 4 5 6 0 1 2 3 4 5 6
R$8.000
R$10.000 R$ 10.000
W
W = 8.000 (1,03)
3
+ 10.000 (1,03)
2
+ 10.000 / (1,03)
1
+
+ 12.000 / (1,03)
2
∴ W = 40.370,70
Exercício 12

15. Prof. Ilydio Sá 15
Exercício 13
Um eletrodoméstico foi comprado de acordo com o fluxo de
caixa apresentado abaixo. Determinar a taxa de juros mensal,
sobre o saldo devedor, inserida no pagamento a prazo.
23,3%éjurosdemensaltaxaaLogo,
1,233
16
14,735
16
2175
F
16
192255
16
(-6).8.4-255
F
06-5F-8F
600F.500F.800
2
2
≅
+
≅
+
=
+±
=
±
=
=
+=
0 1 2
1200
400
500
600
800 Foco
escolhido