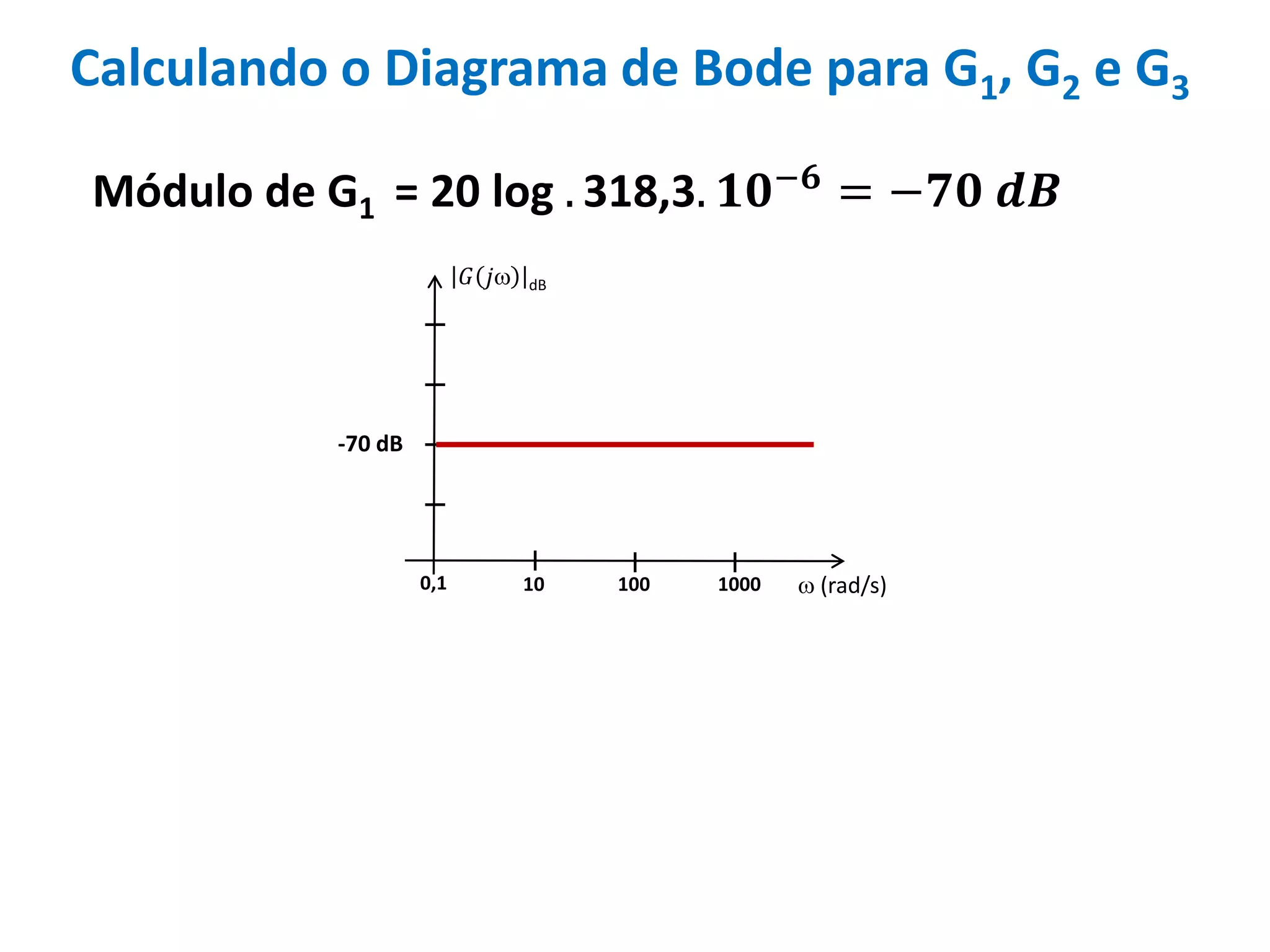
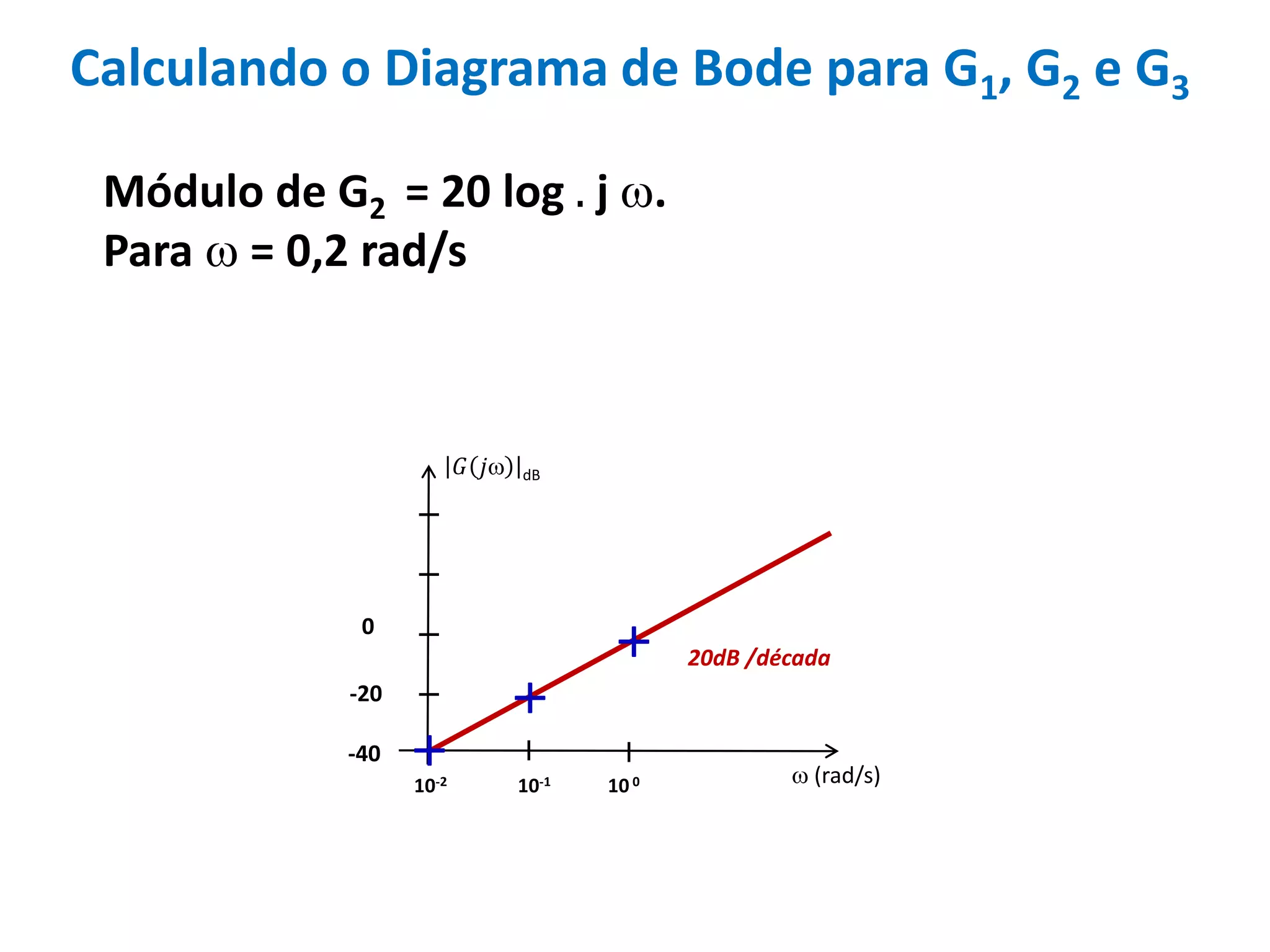
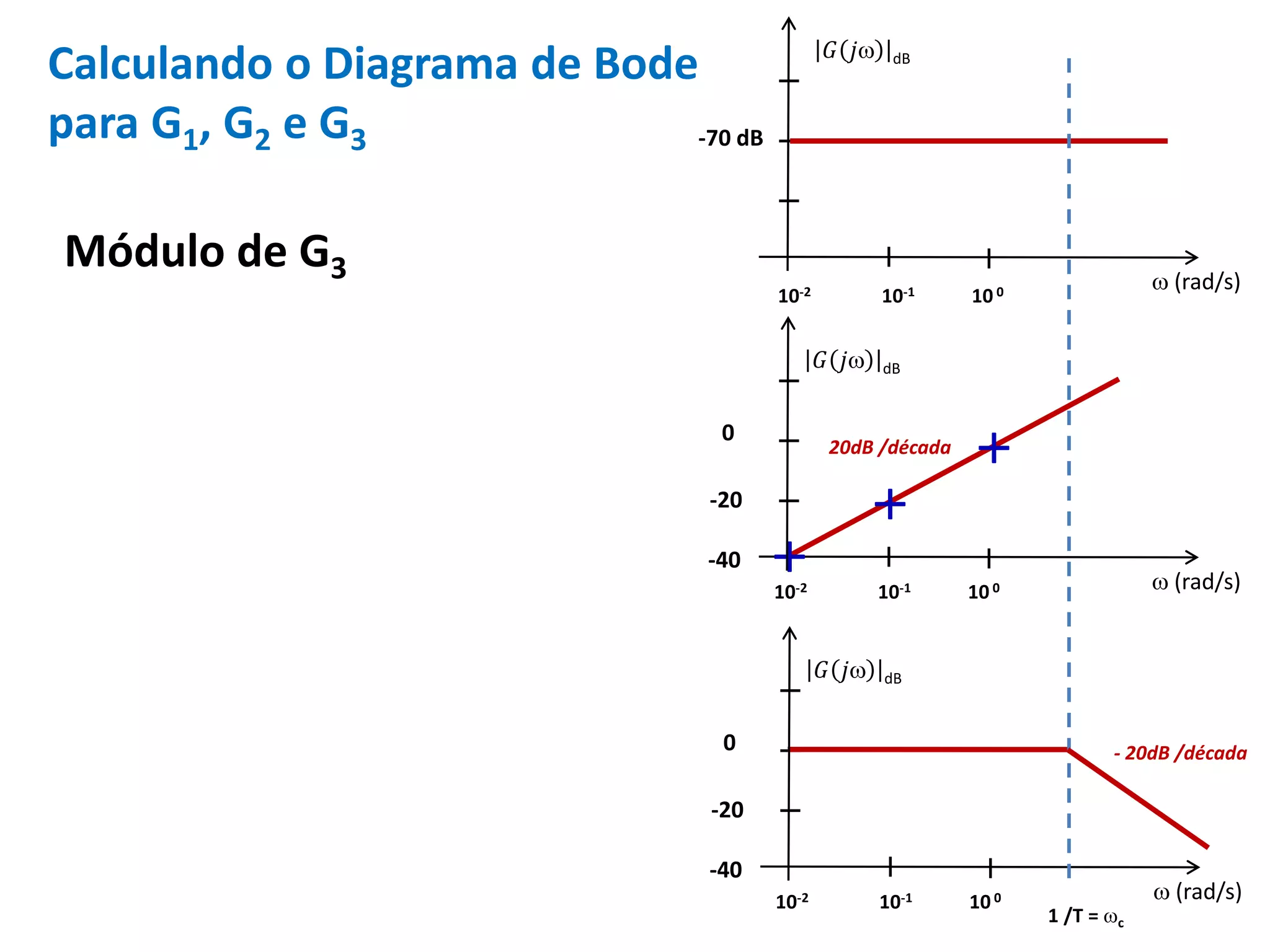
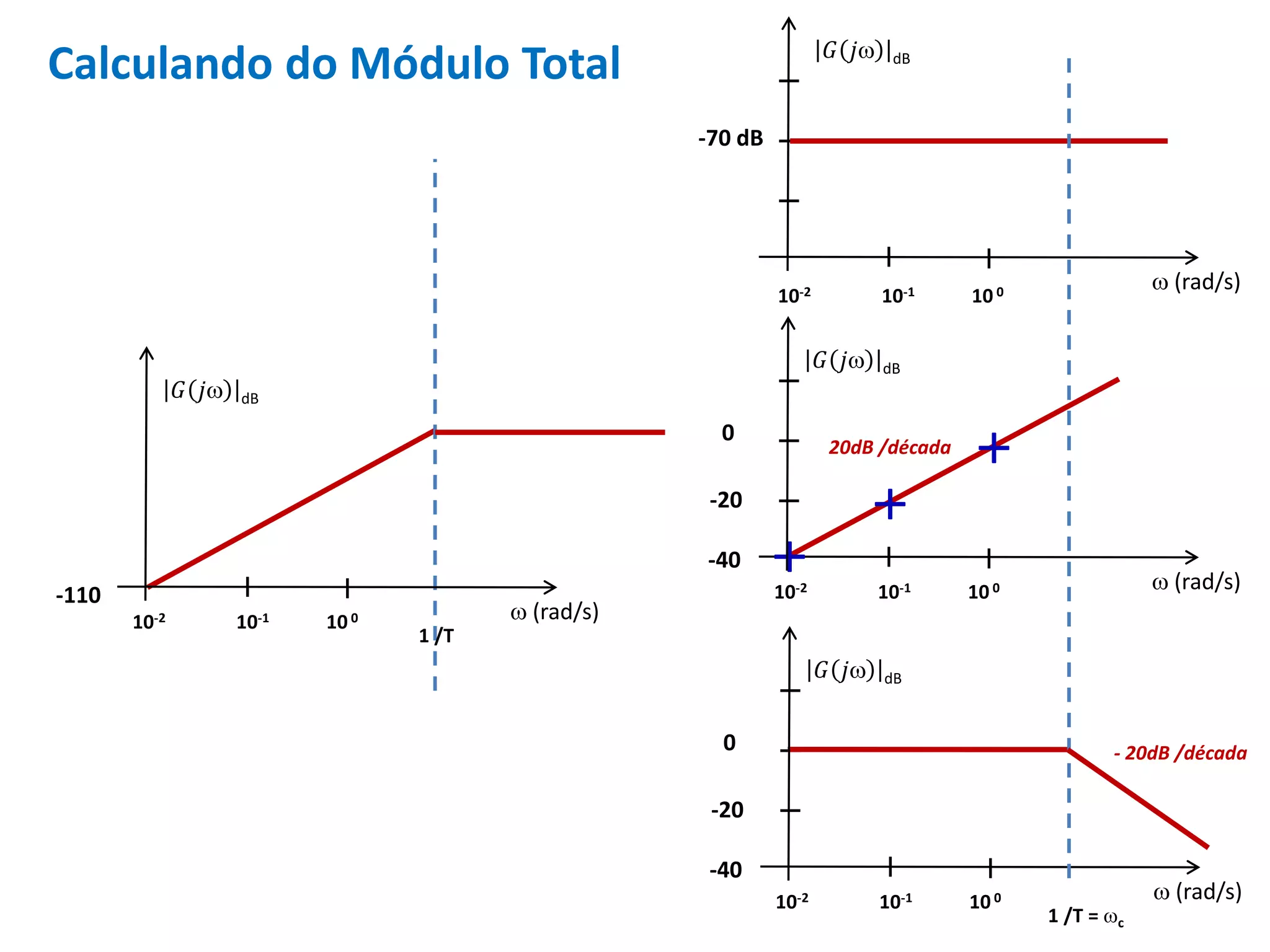
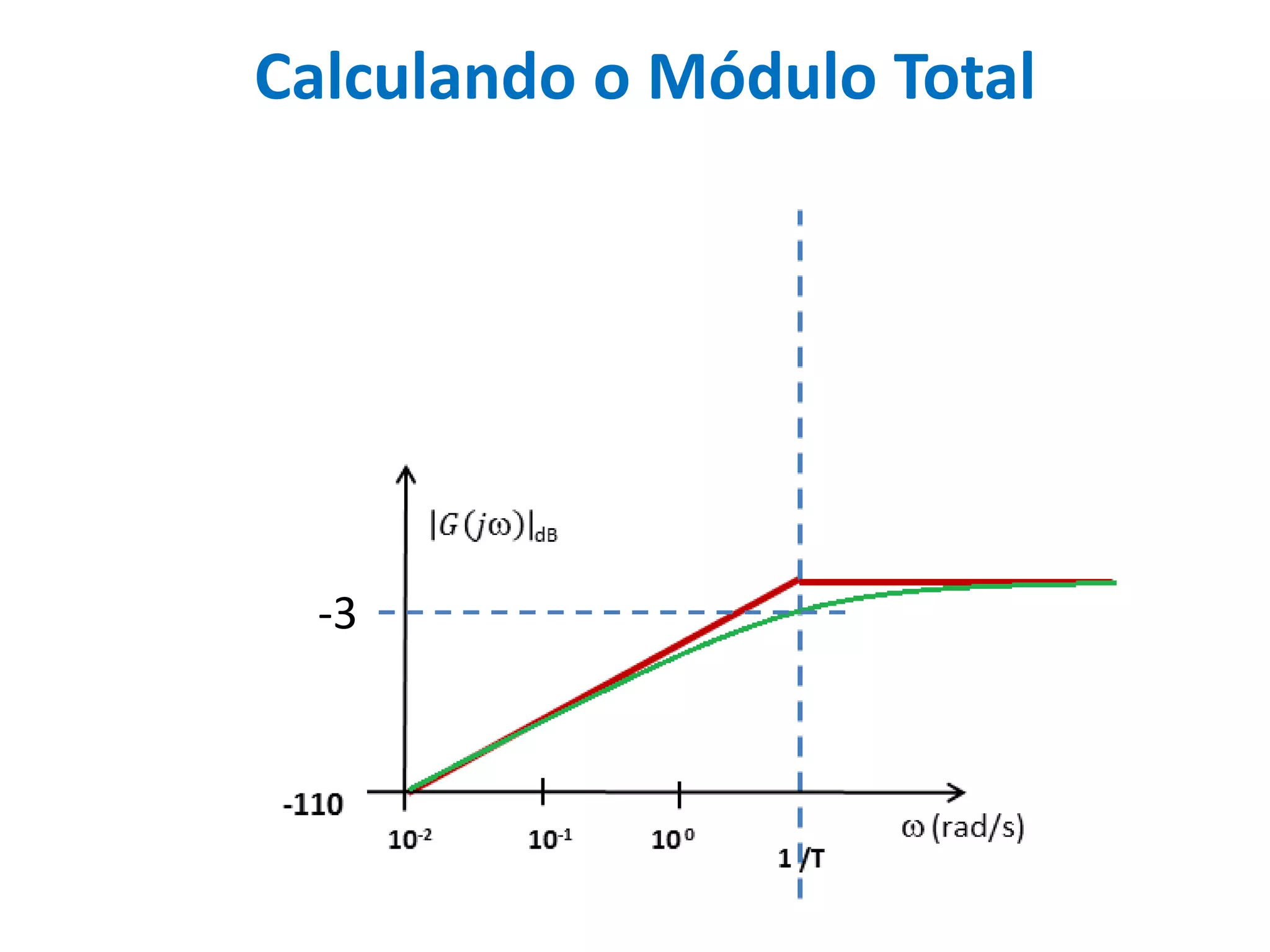
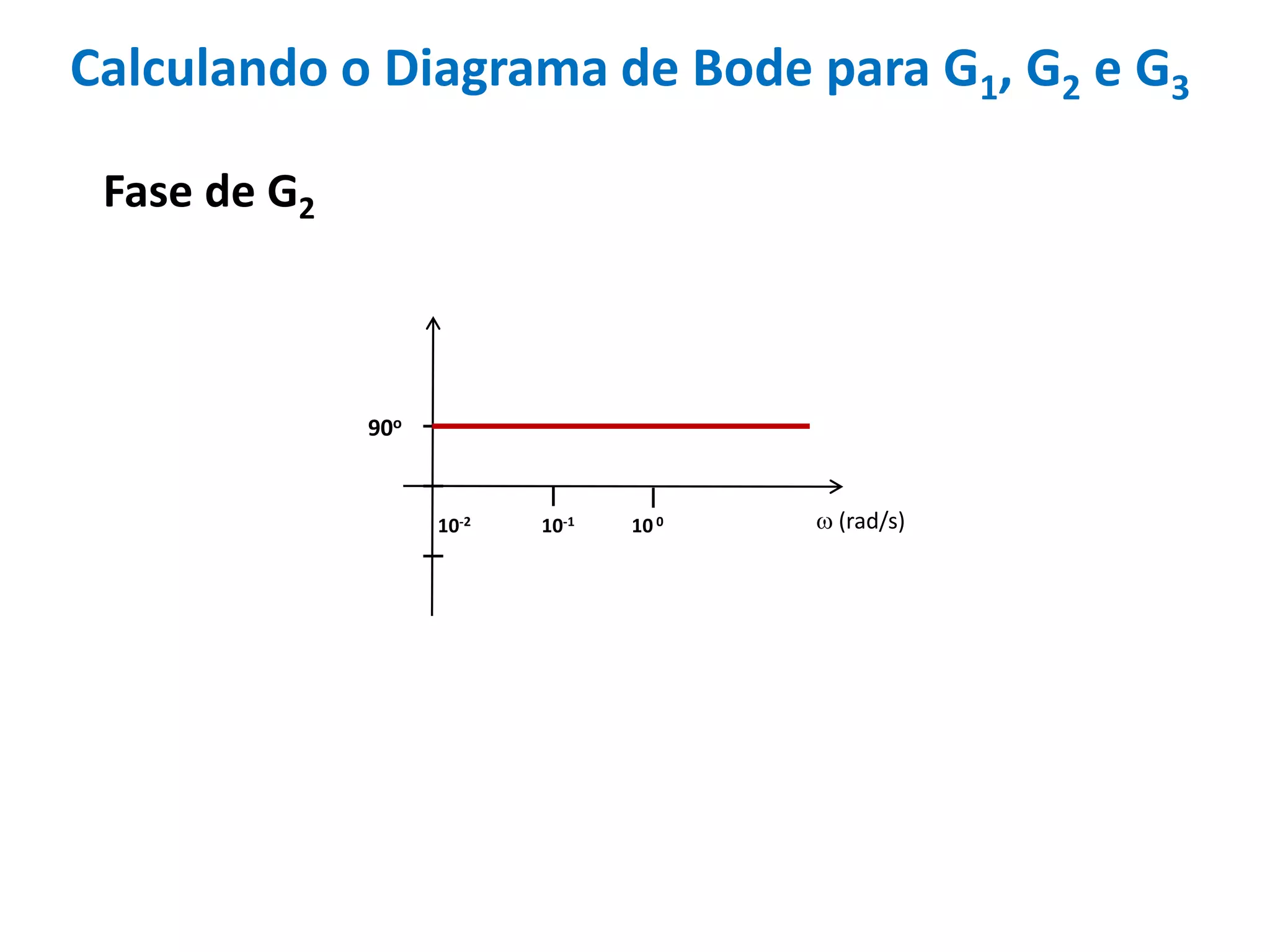
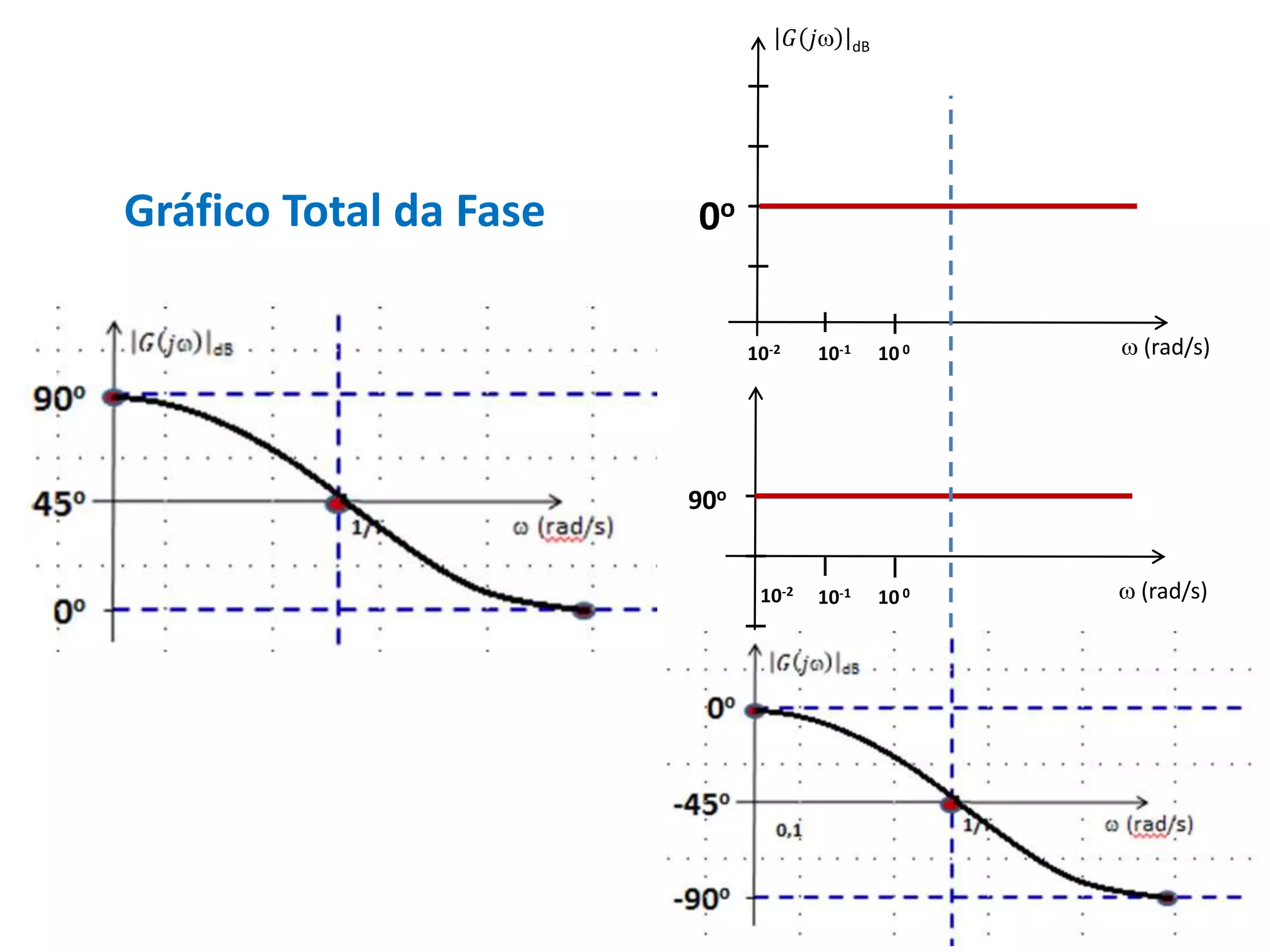
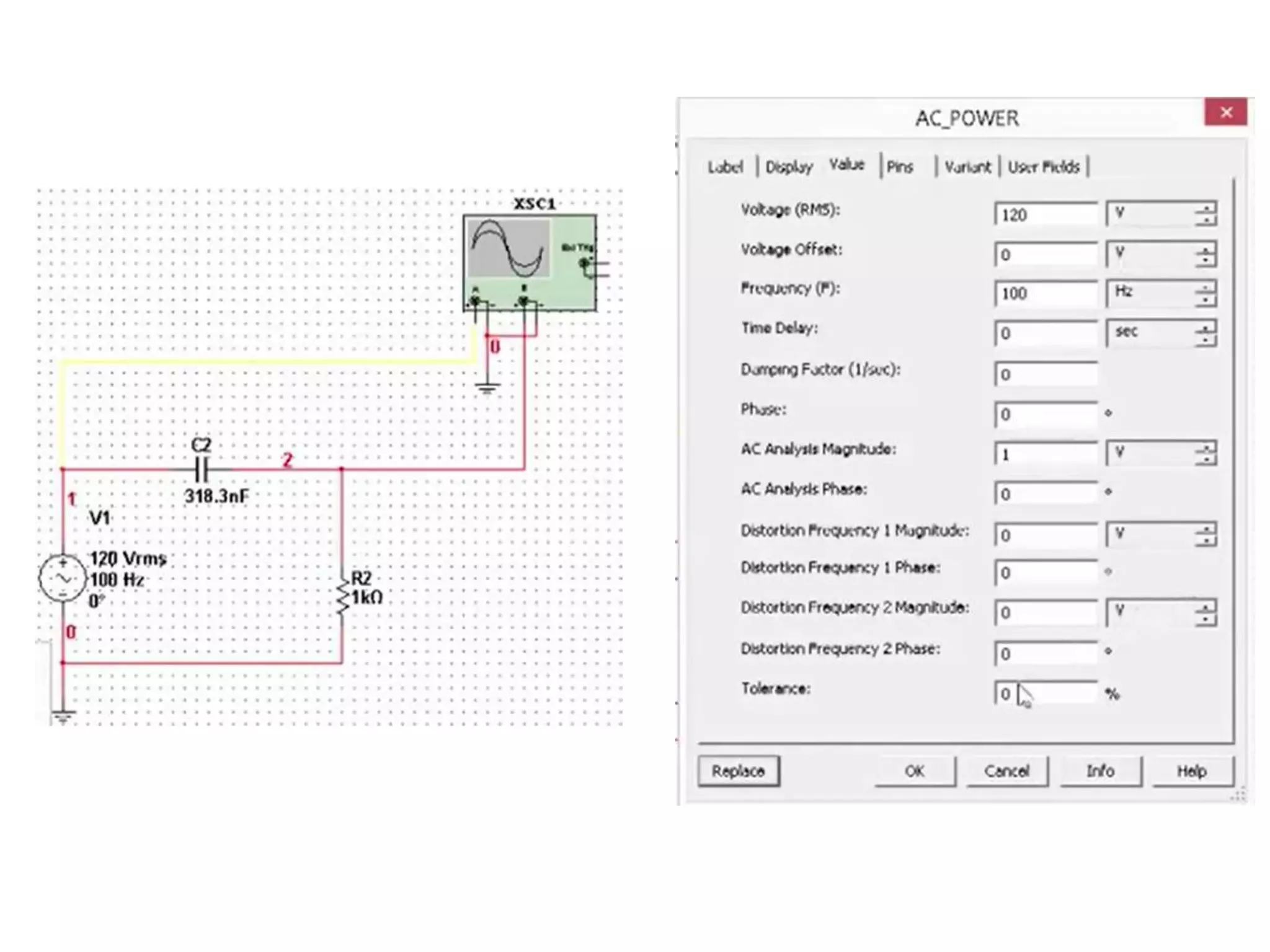
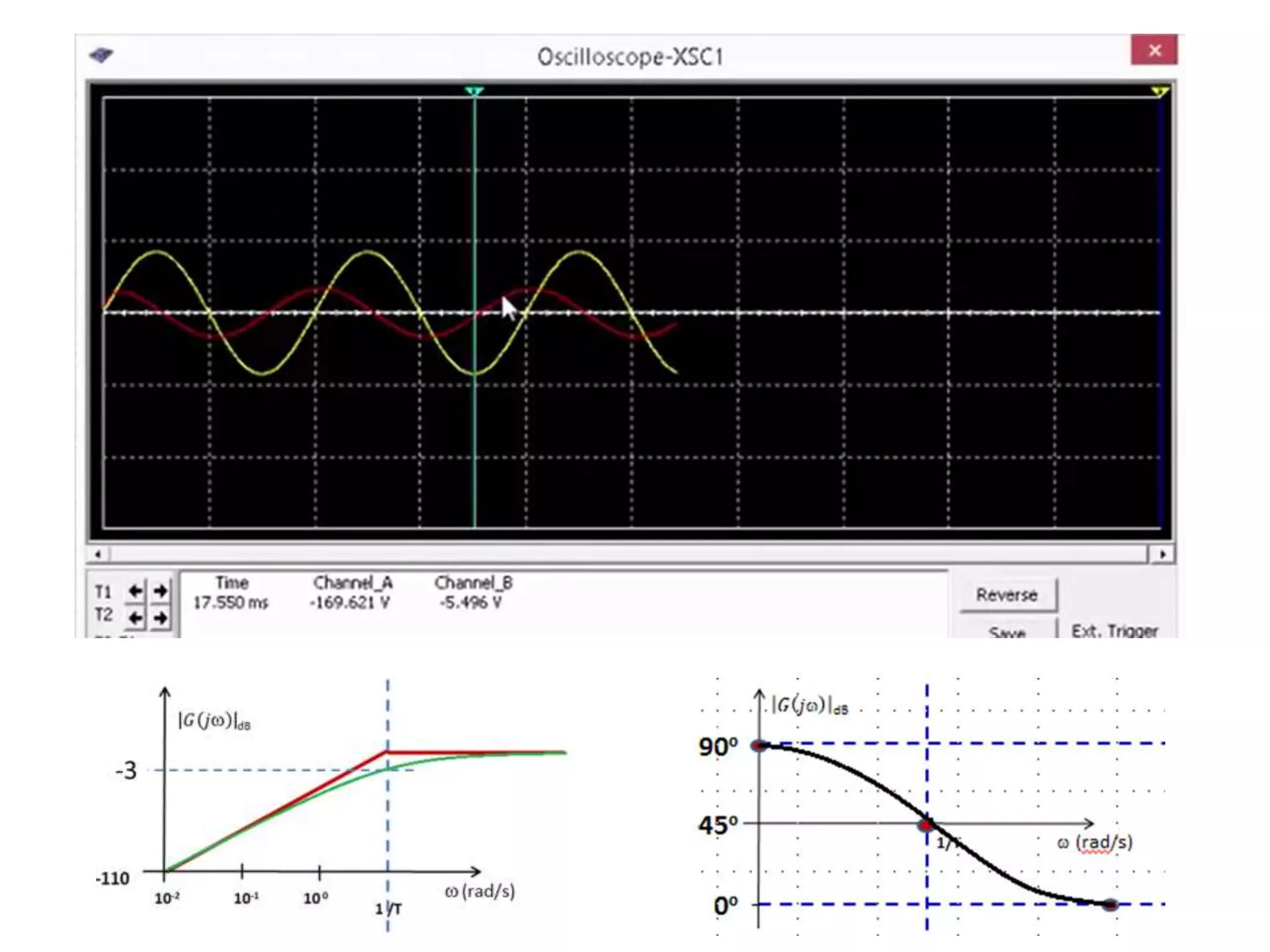
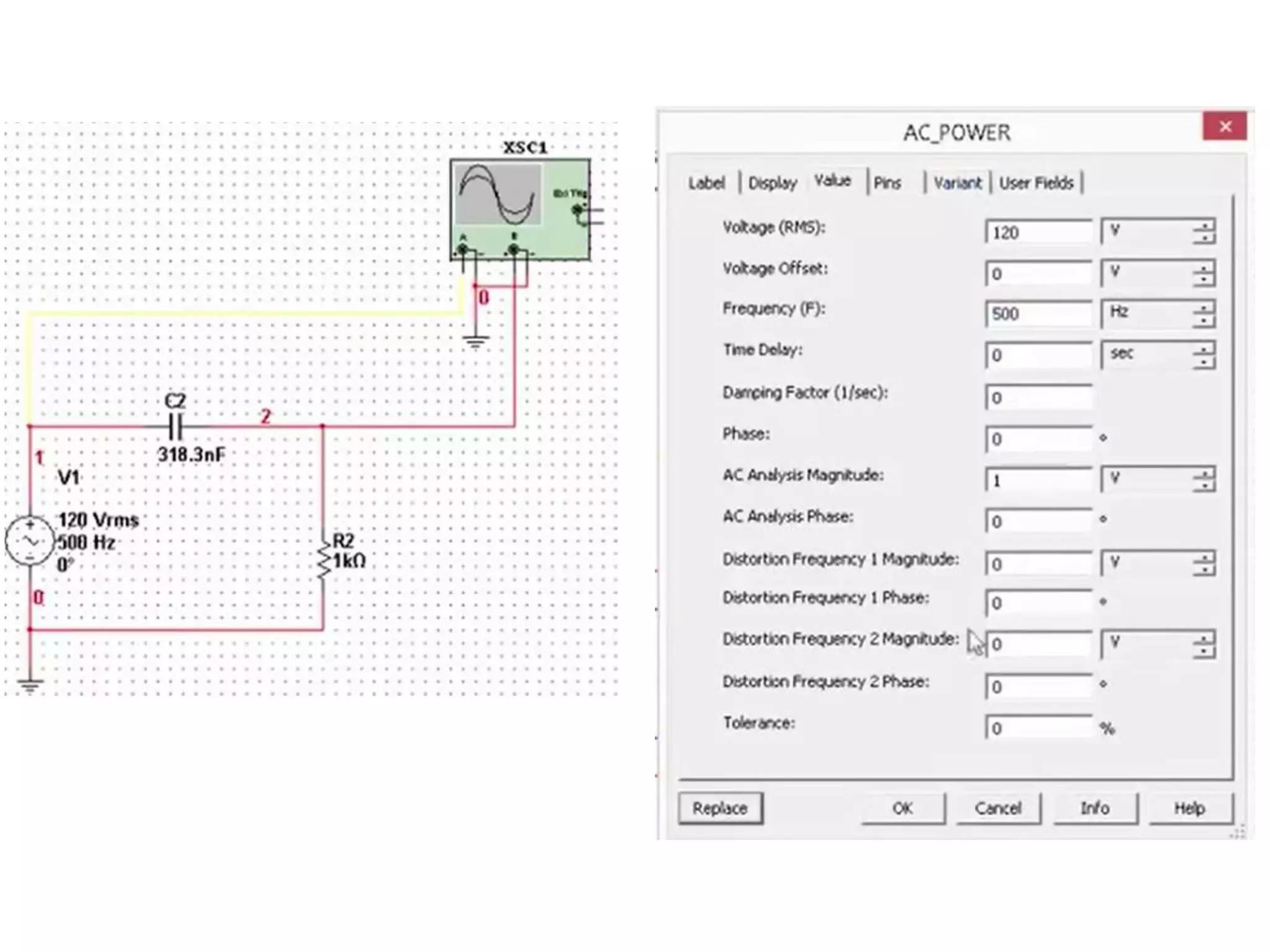
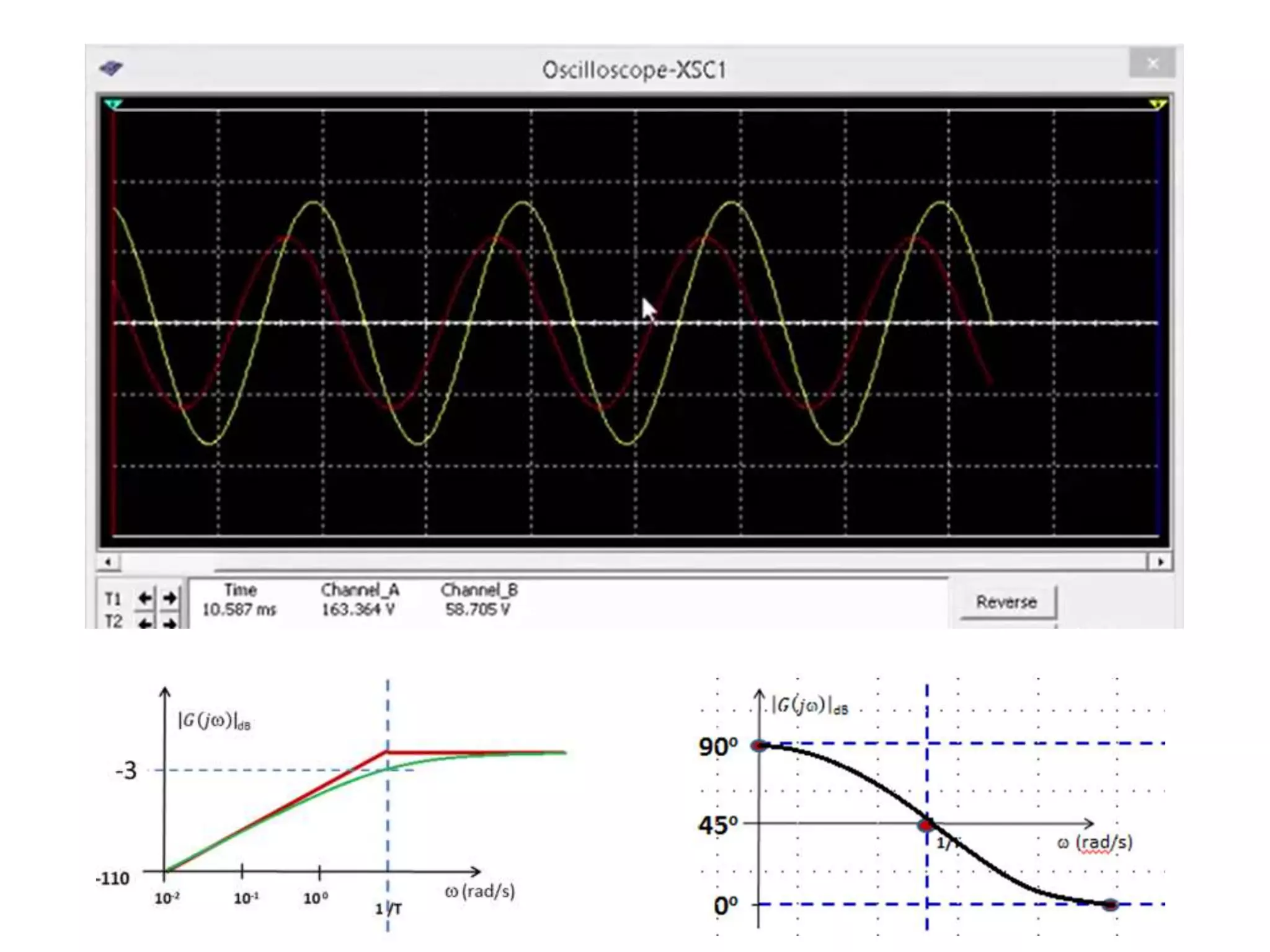
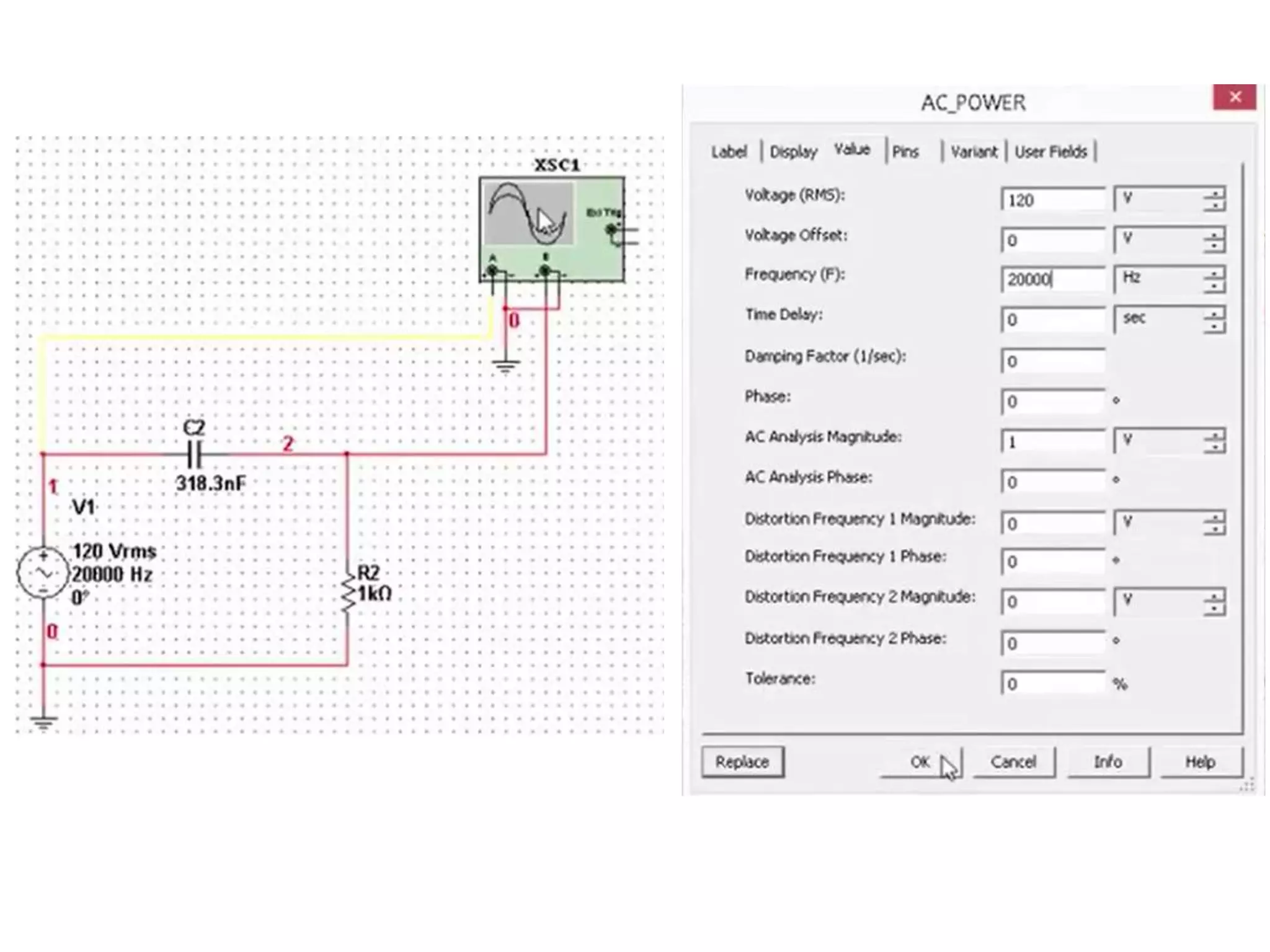
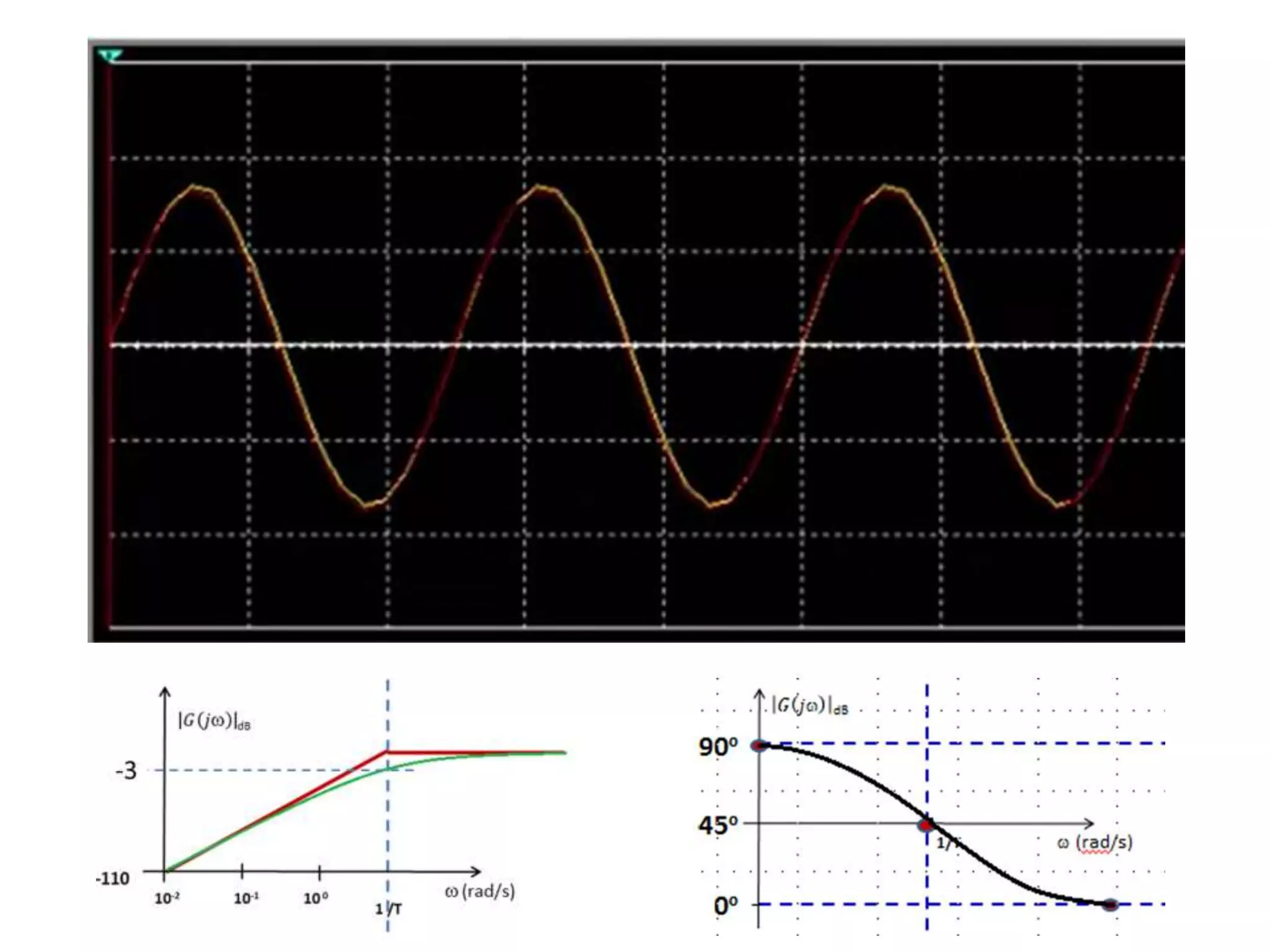
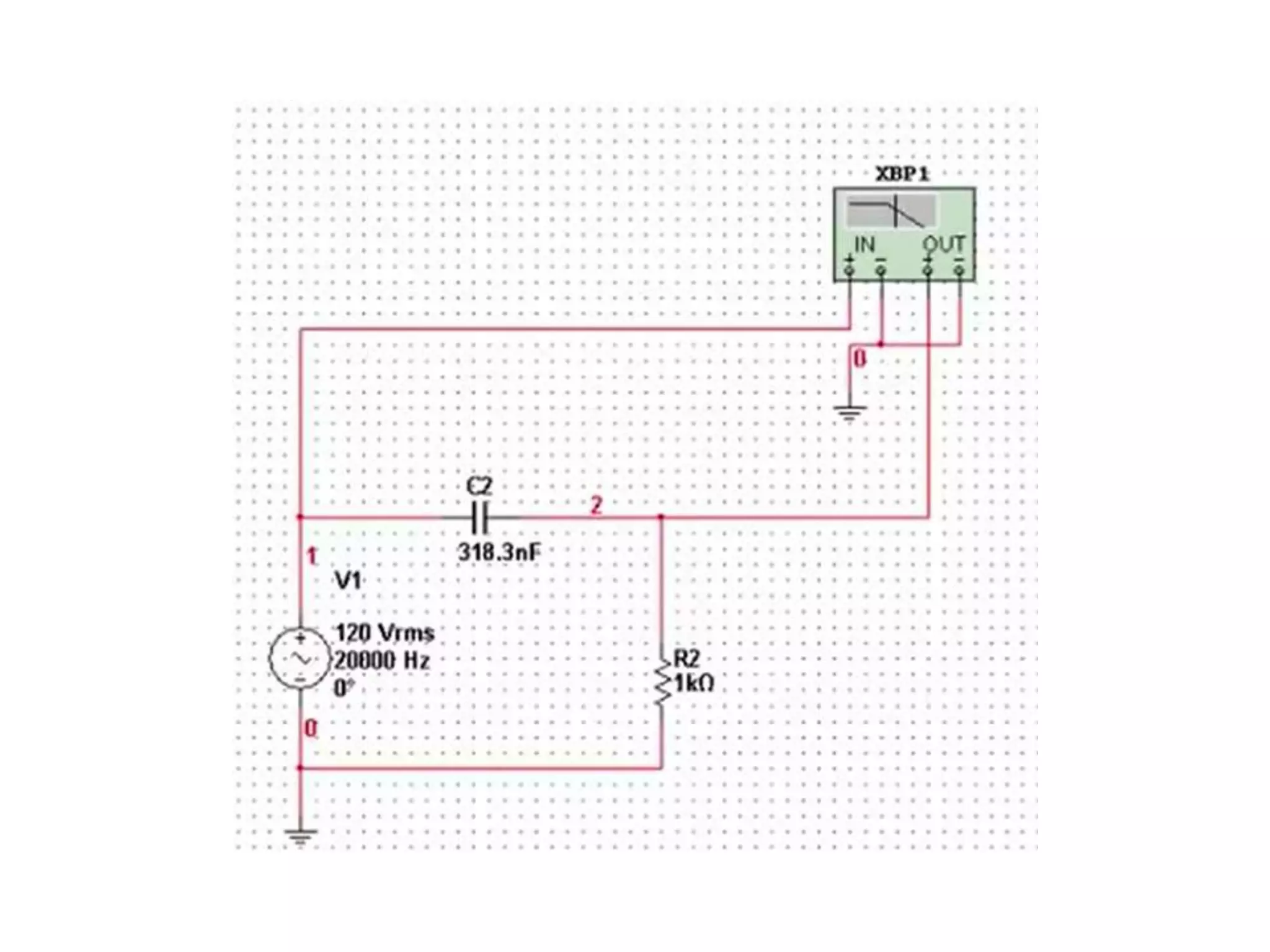
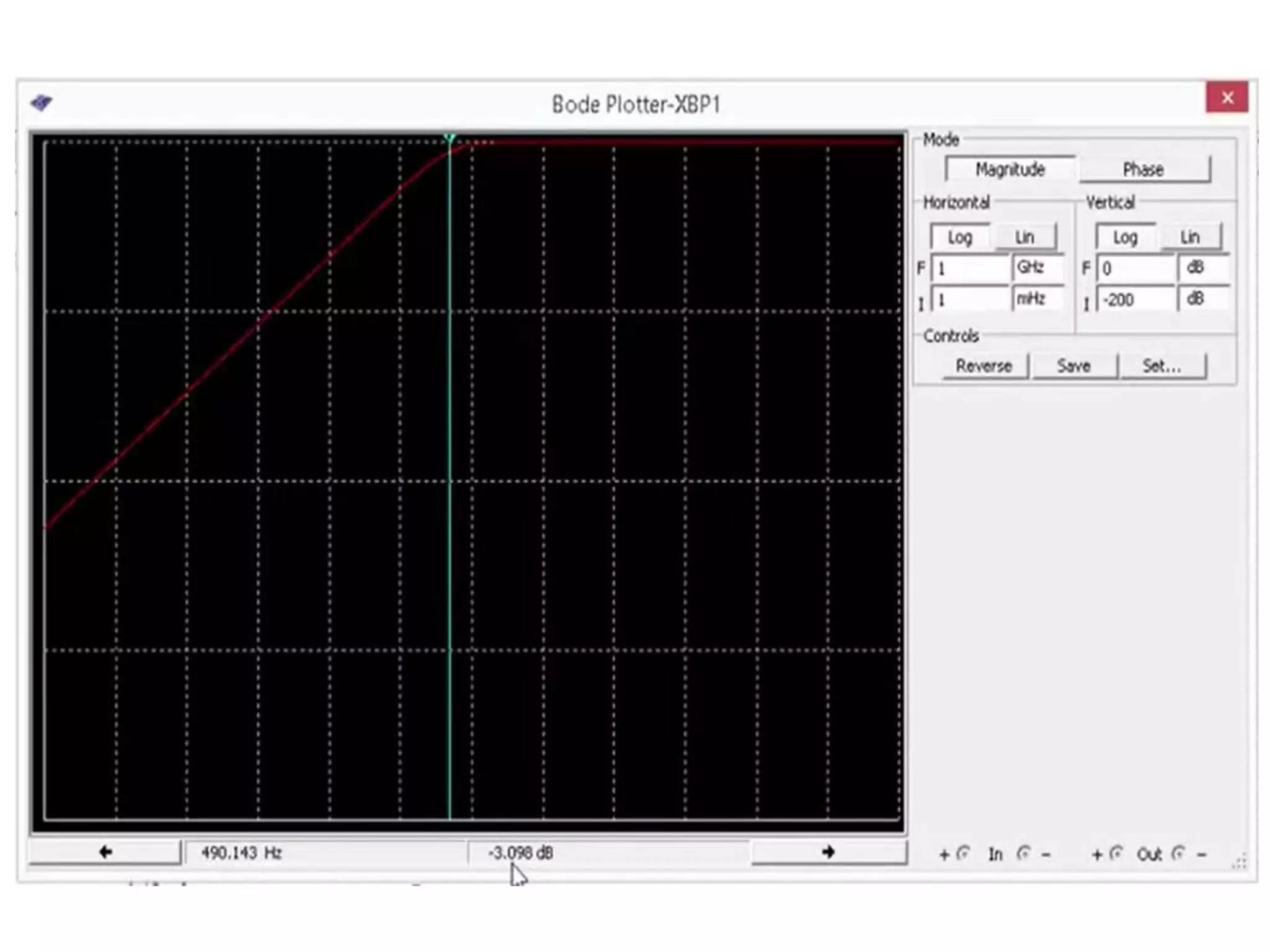
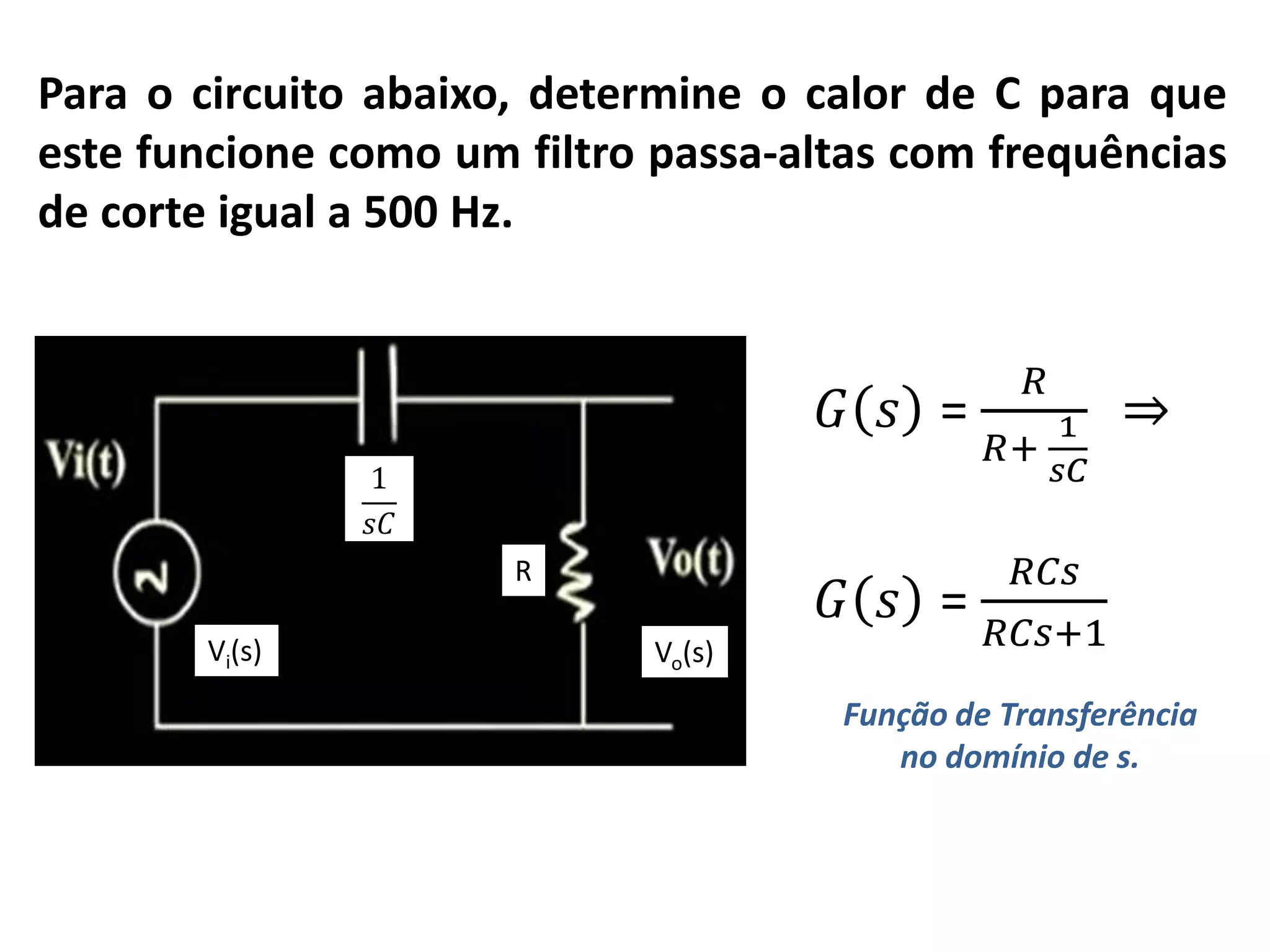
Este documento descreve como calcular o capacitor C para um circuito RC que funciona como um filtro passa-altas com frequência de corte de 500 Hz. Ele calcula o valor de C como 318,3 nF assumindo R = 1 kΩ. Em seguida, desenha os diagramas de Bode para a função de transferência, mostrando a magnitude caindo a -20 dB/década acima da frequência de corte e a fase variando de 0° a 90° entre 10-2 e 100 rad/s.

1. Diagrama de Bode
Exemplo de aplicação

2. Para o circuito abaixo, determine o calor de C para que
este funcione como um filtro passa-altas com frequências
de corte igual a 500 Hz.
1
𝑠𝐶
R
Vi(s) Vo(s)
𝐺 𝑠 =
𝑅
𝑅+
1
𝑠𝐶
𝐺 𝑠 =
𝑅𝐶𝑠
𝑅𝐶𝑠+1
Função de Transferência
no domínio de s.

3. No domínio da frequência, tem-se que a função de
transferência fica com a forma:
𝐺 𝑗 =
𝑅𝐶𝑗
𝑅𝐶𝑗+1
Que pode ser reescrita na forma:
𝐺 𝑗 = 𝑅𝐶 . 𝑗.
1
𝑗 𝑅𝐶+1
Fator de Ganho K
Fator Derivativo Fator de Primeira
Ordem

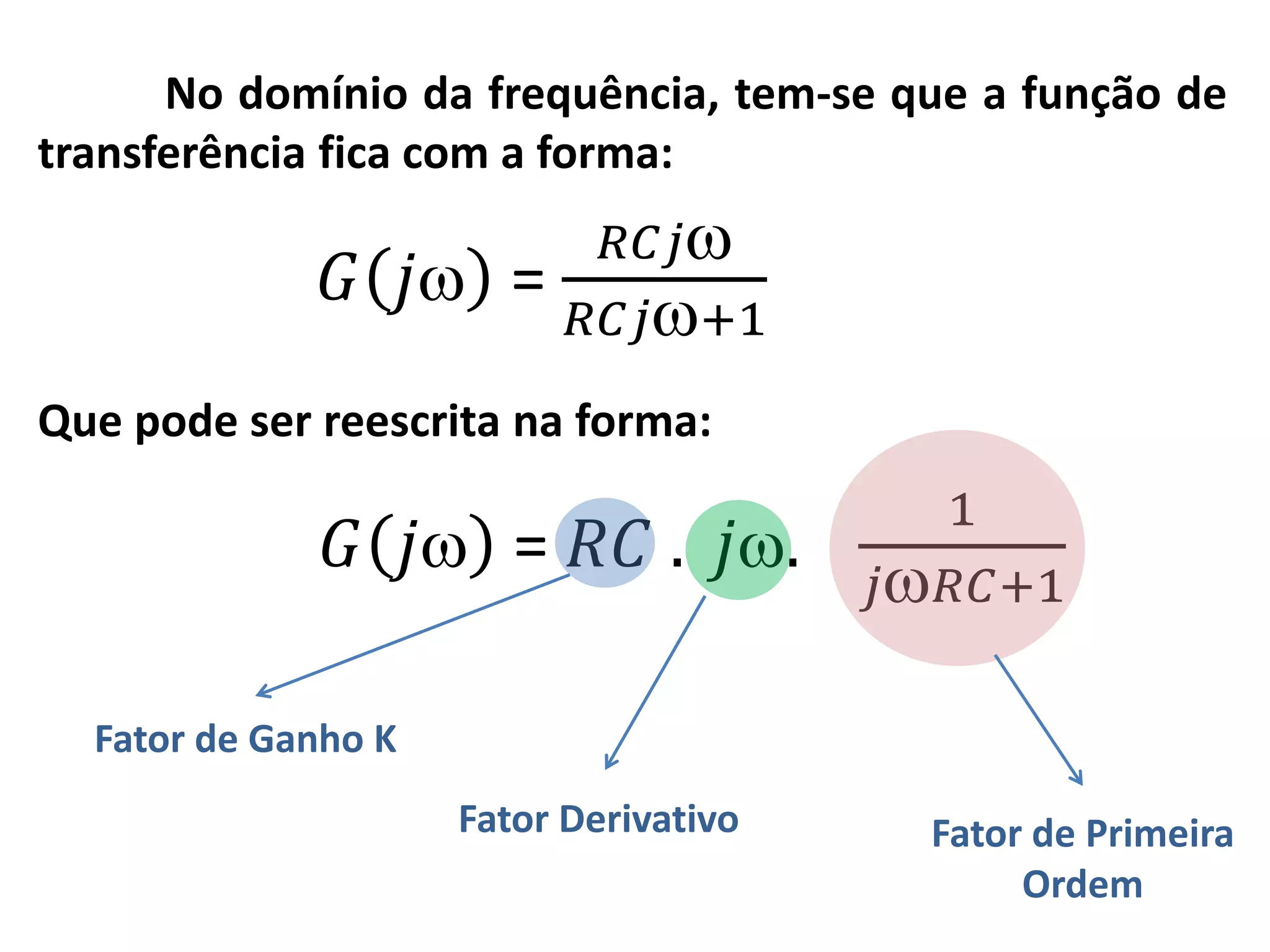
4. Inicialmente, calculamos o valor de RC, começando
pelo fator de primeira ordem. Comparando
Fator de Primeira Ordem
𝐺 𝑗 =
1
𝑗 𝑇 + 1
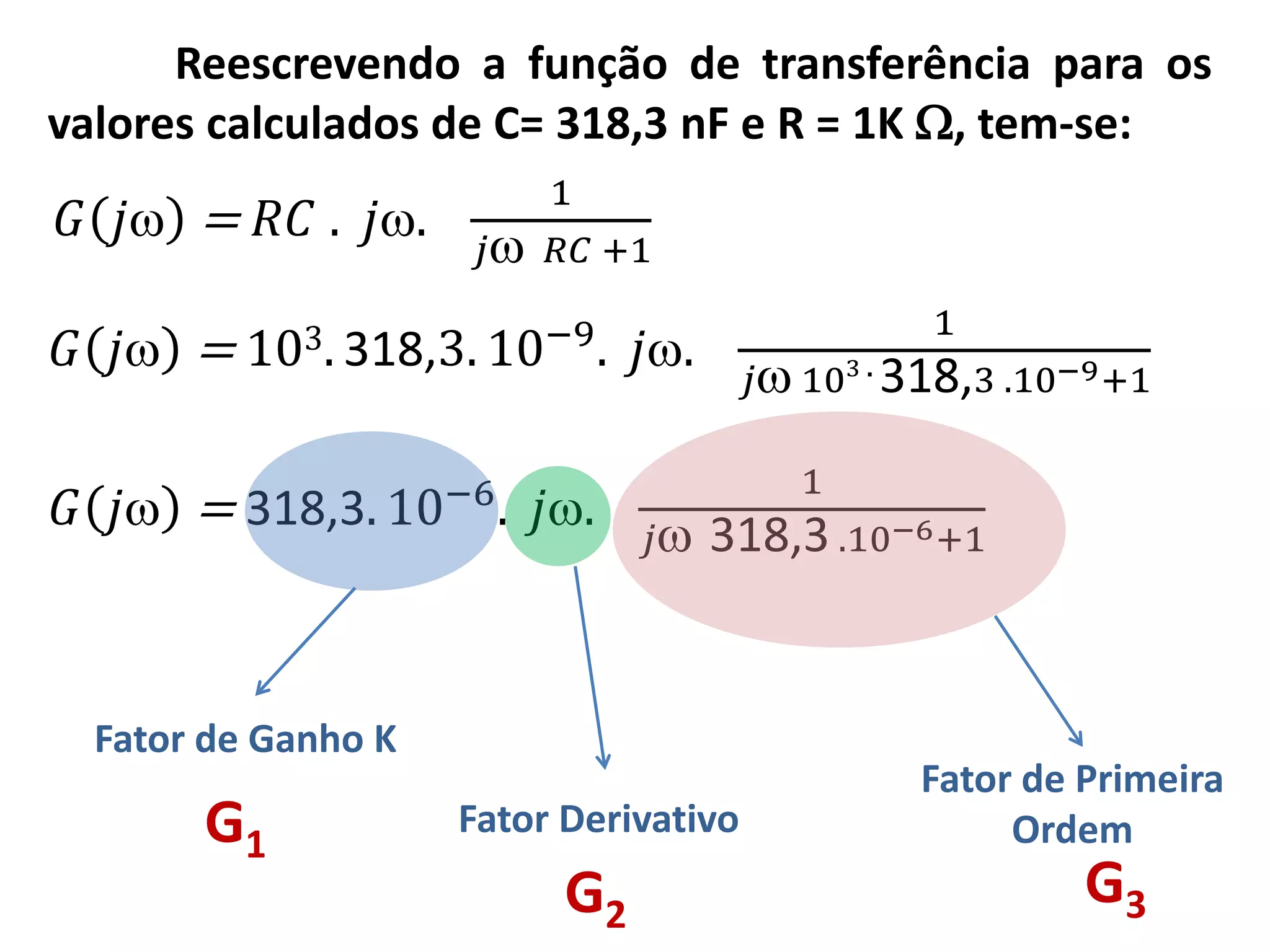
𝐺 𝑗 = 𝑅𝐶 . 𝑗.
1
𝑗 𝑅𝐶 +1
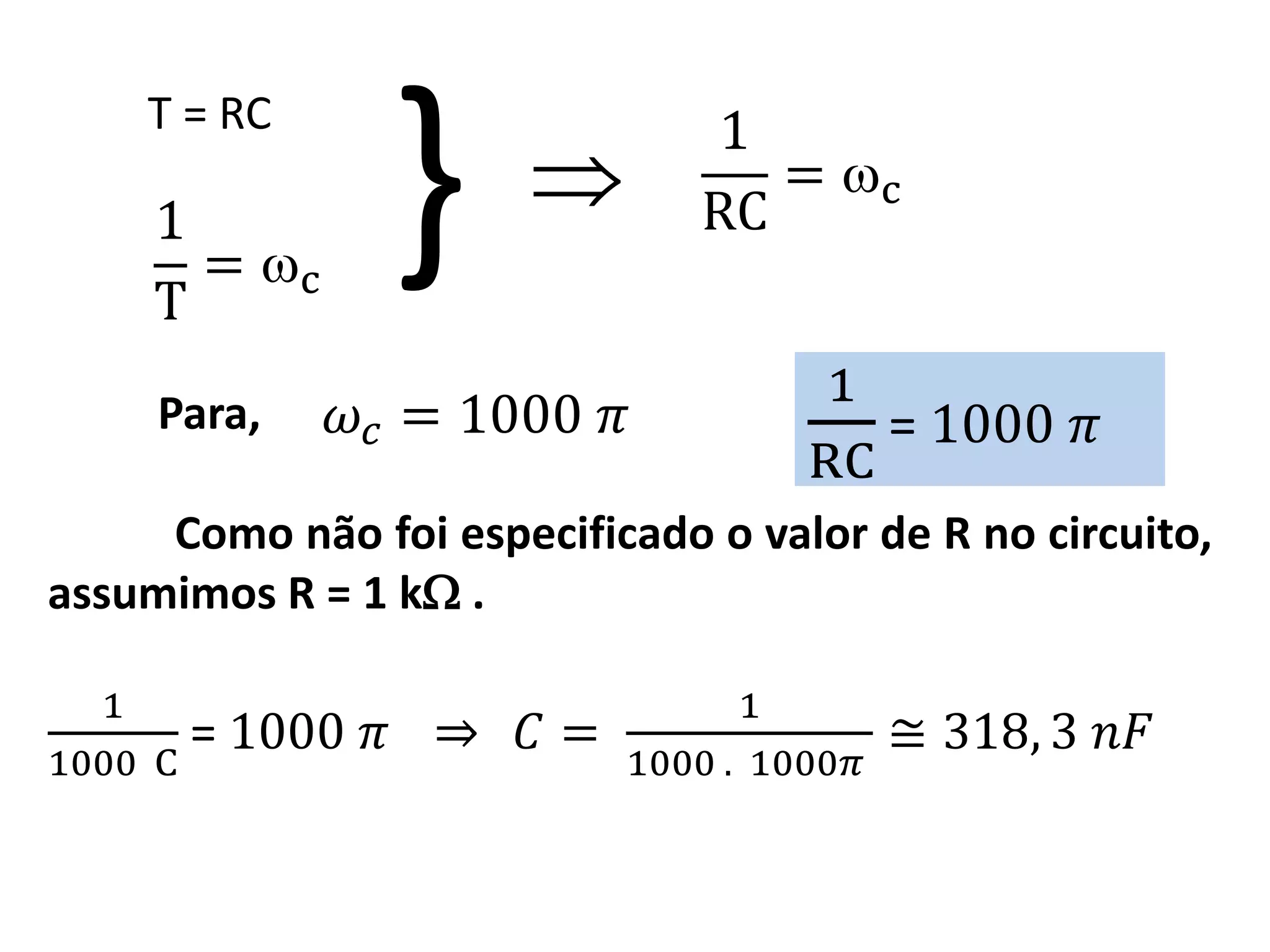
 T = RC
1
𝑇
=  𝑐 = frequência de corteAlém disso,
Como na fórmula [c] = rad / s , há a necessidade
da conversão de 500 Hz para rad/s, ou seja:
𝜔𝑐 = 2𝜋 𝑓𝑐 = 2𝜋 500 = 1000 𝜋

5. T = RC
1
T
= c
𝜔𝑐 = 1000 𝜋
} 
1
RC
= c
Para,
1
RC
= 1000 𝜋
Como não foi especificado o valor de R no circuito,
assumimos R = 1 k .
1
1000 C
= 1000 𝜋 𝐶 =
1
1000 . 1000𝜋
≅ 318, 3 𝑛𝐹

6. Reescrevendo a função de transferência para os
valores calculados de C= 318,3 nF e R = 1K , tem-se:
𝐺 𝑗 = 𝑅𝐶 . 𝑗.
1
𝑗 𝑅𝐶 +1
𝐺 𝑗 = 103. 318,3. 10−9
. 𝑗.
1
𝑗 103 . 318,3 .10−9+1
𝐺 𝑗 = 318,3. 10−6
. 𝑗.
1
𝑗 318,3 .10−6+1
Fator de Ganho K
Fator Derivativo
Fator de Primeira
OrdemG1
G2
G3

7. Calculando o Diagrama de Bode para G1, G2 e G3
Módulo de G1 = 20 log . 318,3. 𝟏𝟎−𝟔 = −𝟕𝟎 𝒅𝑩
 (rad/s)
𝐺 𝑗 dB
0,1 10 100 1000
-70 dB

8. Calculando o Diagrama de Bode para G1, G2 e G3
Módulo de G2 = 20 log . j .
Para  = 0,2 rad/s
 (rad/s)
𝐺 𝑗 dB
10-2
-40
-20
0



10-1 10 0
20dB /década

9. Calculando o Diagrama de Bode
para G1, G2 e G3
Módulo de G3  (rad/s)
𝐺 𝑗 dB
-70 dB
 (rad/s)
𝐺 𝑗 dB
10-2
-40
-20
0



10-1 10 0
10-2 10-1 10 0
 (rad/s)
𝐺 𝑗 dB
10-2
-40
-20
0
10-1 10 0
1 /T = c
- 20dB /década
20dB /década

10. Calculando do Módulo Total
-70 dB
 (rad/s)
𝐺 𝑗 dB
10-2 10-1 10 0
1 /T
-110
 (rad/s)
𝐺 𝑗 dB
 (rad/s)
𝐺 𝑗 dB
10-2
-40
-20
0



10-1 10 0
10-2 10-1 10 0
 (rad/s)
𝐺 𝑗 dB
10-2
-40
-20
0
10-1 10 0
- 20dB /década
20dB /década
1 /T = c

11. Calculando o Módulo Total
-3

12. Calculando o Diagrama de Bode para G1, G2 e G3
Fase de G1
 (rad/s)
𝐺 𝑗 dB
0o
10-2 10-1 10 0

13. Calculando o Diagrama de Bode para G1, G2 e G3
Fase de G2
 (rad/s)
90o
10-2 10-1 10 0

14. Gráfico Total da Fase
 (rad/s)
𝐺 𝑗 dB
0o
10-2 10-1 10 0
 (rad/s)
90o
10-2
10-1 10 0