Carregado porThiago Mosqueiro
2,181 visualizações
Efeito terminônico em tubo
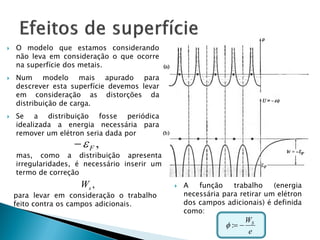
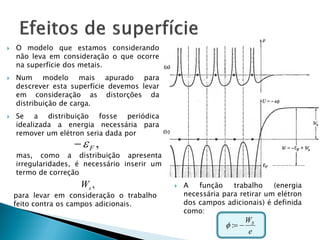
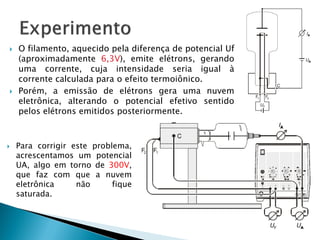
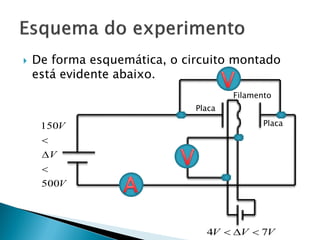
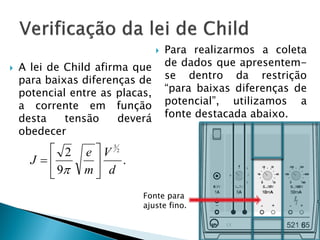
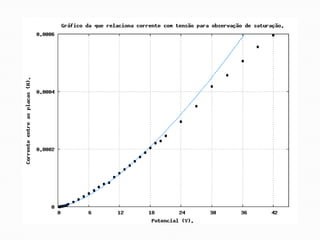
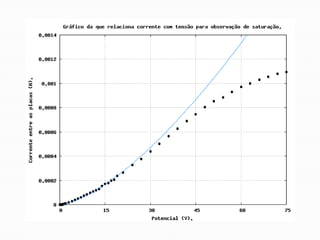
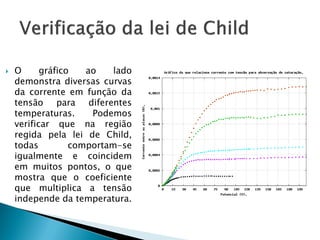
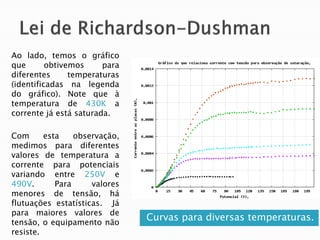
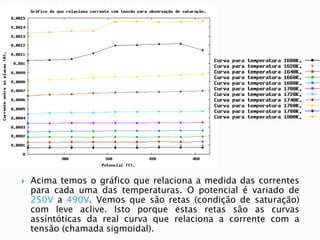
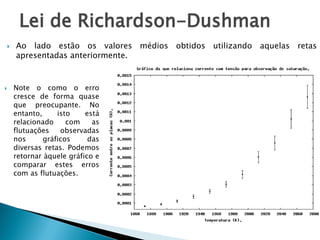
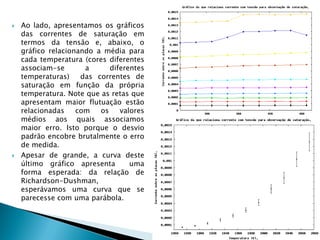
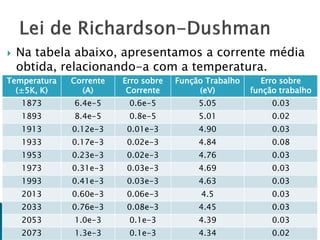
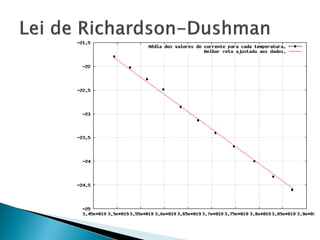
O relatório discute o fenômeno da emissão termiônica, inicialmente descrito por Frederick Guthrie, e sua redescoberta por Thomas Edison e John Ambrose Fleming, que desenvolveram modelos teóricos para explicar a emissão de elétrons. A pesquisa propõe um modelo baseado na estatística de Fermi-Dirac e nas condições do material, destacando a relação entre corrente elétrica e temperatura conforme a Lei de Richardson-Dushman. Além disso, apresenta uma montagem experimental para validar esses modelos e investigar o comportamento de emissões eletrônicas em diferentes temperaturas e tensões.
![[SIFSC] LaTeX para teses e dissertações](https://cdn.slidesharecdn.com/ss_thumbnails/mosqueirosifsc2012latexslideshare-150711235547-lva1-app6891-thumbnail.jpg?width=640&height=640&fit=bounds)
