O documento apresenta comentários sobre questões de métodos quantitativos e raciocínio lógico do concurso para o BNDES, incluindo diversas questões e soluções. Os temas abordam variâncias, correlações, distribuição de frequências e testes de hipóteses. Os autores incentivam os concurseiros a aprenderem com os erros e desejam sucesso nos estudos.

1. mjpio12@gmail.com 1
COMENTÁRIOS DA PROVA DE MÉTODOS QUANTITATIVOS E RACIOCÍNIO LÓGICO
BNDES 2011 ENGENHEIRO – PROF PIO
Prezados concurseiros, segue abaixo os comentários das questões de métodos quantitativos,
matemática financeira e raciocínio lógico propostas pela CESGRANRIO no último concurso para o
BNDES (ENGENHEIRO).
Bons estudos a todos!
APRENDAMOS COM NOSSOS PRÓPRIOS ERROS!!!
31) Ao medir-se a temperatura de um forno, em graus Celsius, em diversos momentos, obteve-se uma
amostra com variância igual a 225. Se cada uma das medidas de temperatura for convertida para graus
Fahrenheit, utilizando-se a fórmula 32C
5
9
F += , o valor da nova variância amostral será
(A) 257
(B) 405
(C) 437
(D) 729
(E) 761
SOLUÇÃO
7299.81225.
25
81
)C(V
5
9
)F(V
2
===





= .
LETRA (D)
32) As variáveis aleatórias X e Y têm variâncias iguais e possuem coeficiente de correlação igual a 0,2. O
coeficiente de correlação entre as variáveis aleatórias X e 5X – 2Y é
(A) – 0,35
(B) – 0,2
(C) 0,1
(D) 0,56
(E) 0,92
SOLUÇÃO
Dados: ( ) 2,0Y,X);Y(DP)X(DP)Y(V)X(V =ρ=⇒=
Pedido: ( )Y2X5,X −ρ
( )
( )
)Y2X5(DP.)X(DP
Y2X5,XCov
Y2X5,X
−
−
=−ρ
Como ( ) )X(V.2,0)Y,X(Cov
)Y(DP.)X(DP
)Y,X(Cov
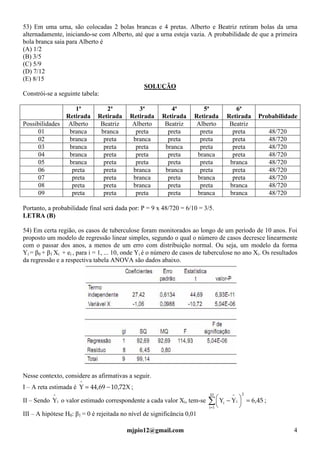
Y,X =⇒=ρ
)X(DP.5)X(V25)Y2X5(DP)X(V25)X(V4)X(V29
)X(V2,0.20)X(V29)Y,X(Cov20)X(V29)Y,X(Cov)2(.5.2)Y(V4)X(V25)Y2X5(V
==−⇒=−
=−=−=−++=−
( ) [ ]
[ ] [ ]
( ) )X(V6,4Y2X5,XCov)X(V6,4)X(V4,0)X(V5
)X(V2,0.2)X(V5)Y,X(Cov2)X(V5)Y(E)X(E2)Y,X(Cov2)Y(E.)X(E2)X(V5
)Y(E)X(E2)Y,X(Cov)Y(E.)X(E2)²X(E²)X(E5)Y(E)X(E2)²X(E5)XY(E2²)X(E5
))Y(E2)X(E5(.)X(E)XY2²X5(E)Y2X5(E.)X(E)Y2X5(.XEY2X5,XCov
=−⇒=−
=−=−=+−−
=++−−=+−−
=−−−=−−−=−
( )
( ) ( ) ( )
92,0
5
6,4
)X(V5
)X(V6,4
)X(V.5
Y2X5,XCov
)X(DP.5.)X(DP
Y2X5,XCov
)Y2X5(DP.)X(DP
Y2X5,XCov
Y2X5,X ===
−
=
−
=
−
−
=−ρ
LETRA (E)

2. mjpio12@gmail.com 2
33) A distribuição de frequências de uma certa amostra é representada no gráfico abaixo.
Sobre a média µ, a mediana m e a moda M dessa amostra, tem-se
(A) m < µ < M
(B) m < M < µ
(C) µ < M < m
(D) M < µ < m
(E) M < m < µ
SOLUÇÃO
Trata-se de uma distribuição com cauda se alongando para a direita, isto é, uma distribuição
assimétrica positiva. Daí, M < m < µ
LETRA (E)
34) Considere as afirmativas a seguir a respeito de três predicados: M, N e P.
• Se algo é M então não é N.
• Se algo não é M então é P.
Analisando-se as afirmações acima, conclui-se que
(A) se algo é N, então é P.
(B) se algo é P, então é N.
(C) se algo é N, então não é P.
(D) se algo não é P, então é N.
(E) se algo não é N, então é P
SOLUÇÃO
Fazendo a contrapositiva de “Se algo é M então não é N” tem-se “Se algo é N, então não é M”.
Como “Se algo não é M então é P”, conclui-se “Se algo é N, então é P”.
LETRA (A)
35) Em uma urna, há um grande número de fichas de quatro tipos: quadradas brancas, quadradas
vermelhas, redondas brancas e redondas vermelhas. Sabe-se que:
• 70% de todas as fichas são brancas.
• 25% das fichas quadradas são vermelhas.
• 60% das fichas vermelhas são redondas.
A porcentagem de fichas redondas e brancas nessa urna é de
(A) 26%
(B) 30%
(C) 34%
(D) 38%
(E) 42%

3. mjpio12@gmail.com 3
SOLUÇÃO
Sejam: X o número total de fichas, Q o número total de fichas quadradas e V o número total de fichas
vermelhas.
Seja o seguinte quadro, preenchido com as informações dadas:
Fichas Quadradas Fichas Redondas
Fichas Brancas 0,75Q 0,7X – 0,75Q
Fichas Vermelhas 0,25Q = 0,4V 0,6V
Como 70% de todas as fichas são brancas, conclui-se que 30% são vermelhas, isto é, V = 0,3X.
Como 0,25Q = 0,4V⇒ 0,25Q = 0,4. 0,3X = 0,12X ⇒ Q = 12X/25.
Portanto, a porcentagem de fichas redondas e brancas será dada por: 0,7X – 0,75Q = 0,7X – 0,75. 12X/25
= 7X/10 – 9X/25 = (35X – 18X)/50 = 17X/50 = 34X/100 = 34%X
LETRA (C)
40) A taxa interna de retorno, de determinado fluxo financeiro,
(A) é sempre maior que a taxa de juros de mercado.
(B) é sempre única.
(C) é negativa se o valor presente líquido do fluxo for negativo.
(D) anula seu valor presente líquido, quando usada para descontá-lo.
(E) nunca pode ser nula.
SOLUÇÃO
Definição de TIR: é a taxa que anula o valor presente líquido (VPL) de um projeto de investimento.
LETRA (D).
44) Uma máquina produz comprimidos de um medicamento. Conforme indicado no rótulo do produto,
cada comprimido deve pesar, em média, 0,5 g. Para testar se a máquina está regulada corretamente, foi
estabelecido um procedimento para testar a hipótese H0 de que a massa média dos comprimidos
produzidos é, de fato, igual a 0,5 g contra a hipótese alternativa H1 de que tal massa é inferior a 0,5 g.
O procedimento de teste consistiu em pesar uma amostra de 100 comprimidos, obter a média m e o desvio
padrão s das massas registradas, em gramas, e rejeitar H0 quando m < 0,5 – 0,15 s. O nível de
significância do teste (ou seja, a probabilidade de se rejeitar a hipótese nula caso ela seja verdadeira) é,
aproximadamente,
(A) 0,059
(B) 0,067
(C) 0,119
(D) 0,134
(E) 0,150
SOLUÇÃO
Tem-se um teste unilateral inferior.
5,0=0μ ;
mX = ;
sS = .
Como n = 100, usa-se a Distribuição Normal.
Rejeita-se H0 quando Z0 < – Zα
Sendo Z0 = (m – 0,5)/0,1s
O problema fornece m < 0,5 – 0,15s ⇒ m – 0,5 < – 0,15s. Dividindo-se ambos os lados por 0,1s, tem-se:
(m – 0,5)/0,1s < – 0,15s/0,1s ⇒ Z0 < –1,5. Consultando a tabela da normal e considerando a simetria,
tem-se que α = 0,067.
LETRA (B)

4. mjpio12@gmail.com 4
53) Em uma urna, são colocadas 2 bolas brancas e 4 pretas. Alberto e Beatriz retiram bolas da urna
alternadamente, iniciando-se com Alberto, até que a urna esteja vazia. A probabilidade de que a primeira
bola branca saia para Alberto é
(A) 1/2
(B) 3/5
(C) 5/9
(D) 7/12
(E) 8/15
SOLUÇÃO
Constrói-se a seguinte tabela:
1ª
Retirada
2ª
Retirada
3ª
Retirada
4ª
Retirada
5ª
Retirada
6ª
Retirada Probabilidade
Possibilidades Alberto Beatriz Alberto Beatriz Alberto Beatriz
01 branca branca preta preta preta preta 48/720
02 branca preta branca preta preta preta 48/720
03 branca preta preta branca preta preta 48/720
04 branca preta preta preta branca preta 48/720
05 branca preta preta preta preta branca 48/720
06 preta preta branca branca preta preta 48/720
07 preta preta branca preta branca preta 48/720
08 preta preta branca preta preta branca 48/720
09 preta preta preta preta branca branca 48/720
Portanto, a probabilidade final será dada por: P = 9 x 48/720 = 6/10 = 3/5.
LETRA (B)
54) Em certa região, os casos de tuberculose foram monitorados ao longo de um período de 10 anos. Foi
proposto um modelo de regressão linear simples, segundo o qual o número de casos decresce linearmente
com o passar dos anos, a menos de um erro com distribuição normal. Ou seja, um modelo da forma
Yi = β0 + β1 Xi + ei , para i = 1, ... 10, onde Yi é o número de casos de tuberculose no ano Xi. Os resultados
da regressão e a respectiva tabela ANOVA são dados abaixo.
Nesse contexto, considere as afirmativas a seguir.
I – A reta estimada é X72,1069,44Y
^
−= ;
II – Sendo i
^
Y o valor estimado correspondente a cada valor Xi, tem-se ∑=
=




 −
10
1i
2
i
^
i 45,6YY ;
III – A hipótese H0: β1 = 0 é rejeitada no nível de significância 0,01

5. mjpio12@gmail.com 5
Está correto o que se afirma em
(A) II, apenas
(B) I e II, apenas
(C) I e III, apenas
(D) II e III, apenas
(E) I, II e III
SOLUÇÃO
I – (F) A reta estimada é X06,142,27Y
^
−= ;
II – (V) Trata-se de SQE = 6,45;
III – (V) Note que 0,01 = 1% é maior que o p-valor = 5,04x10-6
, portanto rejeita-se H0.
LETRA (D)
55) Na cantina de uma fábrica, o lanche constituído de sanduíche e suco custa R$ 4,00. O sanduíche custa
R$ 2,40 a mais que o suco. O preço do suco, em reais, é
(A) 0,80
(B) 1,00
(C) 1,20
(D) 1,40
(E) 1,60
SOLUÇÃO
Seja x o preço do sanduíche e y o preço do suco. Daí, x + y = 4.
x = y + 2,4; y + 2,4 + y = 4; 2y = 4 – 2,4; 2y = 1,6; y = 0,8.
LETRA (A)
56) Míriam, Tereza e Vera possuem, cada uma, um pássaro de estimação. Uma delas tem um canário,
outra, um periquito, e outra, um papagaio. Sabe-se que:
• o periquito não pertence a Míriam;
• Vera não possui o canário;
• Tereza não possui o periquito;
• o papagaio não pertence a Míriam.
Então, é verdade que
(A) Míriam possui o periquito.
(B) Tereza possui o canário.
(C) Vera possui o papagaio.
(D) Míriam não possui o canário.
(E) Tereza possui o papagaio.
SOLUÇÃO
Como o periquito não pertence à Miriam e nem à Tereza, só pode ser de Vera.
Como o papagaio não pertence à Miriam, só pode pertencer à Tereza.
Finalmente, conclui-se que o canário pertence à Miriam. Logo:
Míriam: canário
Tereza: papagaio
Vera: periquito
LETRA (E)

6. mjpio12@gmail.com 6
65) O diagrama abaixo mostra um fluxo financeiro composto de três recebimentos sucessivos, iguais a
R$ 10,00, seguidos de um último recebimento de R$ 110,00, após quatro períodos.
Se a taxa de juros compostos usada for de 10% por período, o valor presente líquido desse fluxo de
recebimentos, em reais, será de
(A) 90,00
(B) 100,00
(C) 110,00
(D) 130,00
(E) 140,00
SOLUÇÃO
Note que se trata de uma capitalização composta que pelo fato de termos recebimentos de R$ 10,00
se transforma em uma capitalização simples, isto é, não há capitalização de juros sobre juros. Logo,
sendo a taxa de 10% por período, tem-se que VPL = R$ 100,00.
LETRA (B)
67) Sérgio, Julia e Marcelo estão juntos, nessa ordem, em uma fila. Sérgio diz: “O número de pessoas que
está atrás de mim é o triplo do número de pessoas que está à minha frente.” Marcelo diz: “O número de
pessoas que está atrás de mim é o dobro do número de pessoas que está à minha frente.” O número de
pessoas dessa fila é
(A) 16
(B) 18
(C) 20
(D) 25
(E) 28
SOLUÇÃO
Suponha a seguinte fila: x pessoas, Sérgio, Julia, Marcelo, y pessoas. Do enunciado tem-se:
y + 2 = 3x; y = 3x – 2;
y = 2(x + 2);
3x – 2 = 2x + 4; x = 6; y = 16. Portanto, teremos na fila 6 + 16 + 3 = 25 pessoas.
LETRA (D)
Um boa sorte à todos!!! NÃO DESANIMEM!!!! Vamos em frente!!!
Fiquem com DEUS!!!
Um abraço, Prof Pio.