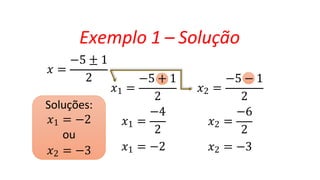
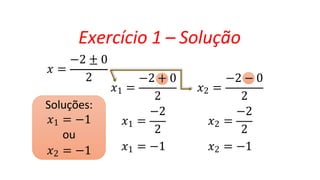
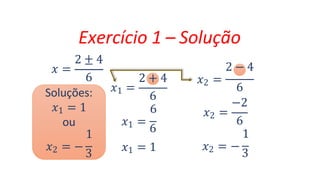
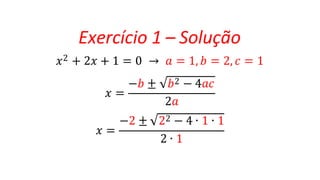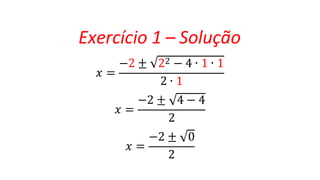O documento explica a fórmula de Bhaskara, que é usada para resolver equações do segundo grau. A fórmula é derivada através de uma série de passos algebraicos, começando com ax2 + bx + c = 0. O discriminante, representado por Δ, é uma parte importante da fórmula, determinando se a equação tem soluções reais ou complexas. Exemplos demonstram como aplicar a fórmula e calcular o discriminante.

1. MATEMÁTICA
9º ANO
Thalles Rannieri
EQUAÇÕES DO 2º GRAU - A FÓRMULA DE
BHASKARA

2. A Fórmula Resolutiva
(Fórmula de Bhaskara)
É comum ouvir que a fórmula geral para a
resolução de equações do 2º grau com uma
incógnita foi determinada pelo matemático
indiano Bhaskara, no século XII.

3. Equação do 2º grau completa
No Brasil a fórmula resolutiva utilizada para
determinar a solução de uma equação do 2º
grau com uma incógnita é popularmente
conhecida como a Fórmula de Bhaskara.

4. Conhecendo a fórmula...
Considere a equação 𝒂𝒙² + 𝒃𝒙 + 𝒄 = 𝟎 ,
com 𝑎 ≠ 0, 𝑏 e 𝑐 ∈ ℝ.
𝟏º Passo: Isolamos o termo 𝒄.
𝒂𝒙² + 𝒃𝒙 + 𝒄 = 𝟎
𝒂𝒙² + 𝒃𝒙 = −𝒄

5. Conhecendo a fórmula...
𝟐º Passo: Para que o termo 𝒂𝒙² represente
um termo de um trinômio quadrado perfeito,
multiplicamos os dois membros da igualdade
por 𝟒𝒂.
𝟒𝒂
𝒂𝒙² + 𝒃𝒙 = −𝒄
∙ 𝒂𝒙𝟐 + 𝒃𝒙 = (𝟒𝒂) ∙ (−𝒄)
𝟒𝒂²𝒙𝟐 + 𝟒𝒂𝒃𝒙 = −𝟒𝒂𝒄

6. Conhecendo a fórmula...
𝟑º Passo: Adicionamos 𝒃² aos dois
membros da igualdade para que o primeiro
membro represente um trinômio quadrado
perfeito.
𝟒𝒂²𝒙𝟐 + 𝟒𝒂𝒃𝒙 = −𝟒𝒂𝒄
𝟒𝒂²𝒙𝟐 + 𝟒𝒂𝒃𝒙 + 𝒃² = 𝒃² − 𝟒𝒂𝒄

7. Conhecendo a fórmula...
𝟒º Passo: Fatoramos o primeiro membro.
𝟒𝒂²𝒙𝟐 + 𝟒𝒂𝒃𝒙 + 𝒃² = 𝒃² − 𝟒𝒂𝒄
𝟐𝒂𝒙 + 𝒃 𝟐 = 𝒃𝟐 − 𝟒𝒂𝒄
𝑎 + 𝑏 2 = 𝑎² + 2𝑎𝑏 + 𝑏2
Produto Notável

8. Conhecendo a fórmula...
𝟓º Passo: Extraímos a raiz quadrada de
ambos os membros da igualdade.
2𝑎𝑥 + 𝑏 2 = 𝑏2 − 4𝑎𝑐
2 =
2𝑎𝑥 + 𝑏 𝑏2 − 4𝑎𝑐
2𝑎𝑥 + 𝑏 = ± 𝑏2 − 4𝑎𝑐

9. Conhecendo a fórmula...
𝟔º Passo: Passamos 𝒃 para o segundo
membro.
2𝑎𝑥 + 𝑏 = ± 𝑏2 − 4𝑎𝑐
2𝑎𝑥 = −𝒃 ± 𝑏2 − 4𝑎𝑐

10. Conhecendo a fórmula...
7º Passo: Dividimos os dois membros por 𝟐𝒂.
2𝑎𝑥 = −𝑏 ±
2𝑎
=
2𝑎𝑥 −𝑏 ±
𝑏2 − 4𝑎𝑐
𝑏2 − 4𝑎𝑐
𝑥 =
−𝑏 ±
2𝑎
𝑏2 − 4𝑎𝑐
2𝑎
Fórmula de
Bhaskara

11. Exemplo 1
Resolva a equação do 2º grau a seguir:
𝑥2 + 5𝑥 + 6 = 0
𝑎 = 1, 𝑏 = 5, 𝑐 = 6
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎

12. Exemplo 1 – Solução
𝑥2 + 5𝑥 + 6 = 0 → 𝑎 = 1, 𝑏 = 5, 𝑐 = 6
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
𝑥 =
2𝑎
−5 ± 52 − 4 ∙ 1 ∙ 6
2 ∙ 1

13. Exemplo 1 – Solução
𝑥 =
−5 ± 52 − 4 ∙ 1 ∙ 6
𝑥 =
2 ∙ 1
−5 ± 25 − 24
𝑥 =
2
−5 ± 1
2

14. Exemplo 1 – Solução
𝑥 =
−5 ± 1
2
−5 ± 1
𝑥 =
2

15. Exemplo 1 – Solução
𝑥 =
−5 ± 1
2
𝑥1 =
2
−4
𝑥1 =
2
𝑥1 = −2
𝑥2 =
−5 + 1 −5 − 1
2
−6
𝑥2 =
2
𝑥2 = −3
Soluções:
𝑥1 = −2
ou
𝑥2 = −3

16. Exercício 1
Resolva a equação do 2º grau a seguir:
𝑥2 + 2𝑥 + 1 = 0
𝑎 = 1, 𝑏 = 2, 𝑐 = 1
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎

17. Exercício 1 – Solução
𝑥2 + 2𝑥 + 1 = 0 → 𝑎 = 1, 𝑏 = 2, 𝑐 = 1
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
𝑥 =
2𝑎
−2 ± 22 − 4 ∙ 1 ∙ 1
2 ∙ 1

18. Exercício 1 – Solução
𝑥 =
−2 ± 22 − 4 ∙ 1 ∙ 1
2 ∙ 1
𝑥 =
−2 ± 4 − 4
𝑥 =
2
−2 ± 0
2

19. Exercício 1 – Solução
𝑥 =
−2 ± 0
2
−2 ± 0
𝑥 =
2

20. Exercício 1 – Solução
𝑥 =
−2 ± 0
2
𝑥1 =
2
−2
𝑥1 =
2
𝑥1 = −1
𝑥2 =
−2 + 0 −2 − 0
2
−2
𝑥2 =
2
𝑥2 = −1
Soluções:
𝑥1 = −1
ou
𝑥2 = −1

21. Fórmula de Bhaskara
Discriminante da equação...
𝒙 =
−𝒃 ± 𝒃𝟐 − 𝟒𝒂𝒄
𝟐𝒂
∆= 𝒃𝟐 − 𝟒𝒂𝒄

22. Fórmula de Bhaskara
Discriminante da equação...
A expressão 𝒃𝟐 − 𝟒𝒂𝒄 é chamada
discriminante da equação, por convenção é
letra grega ∆
costume representá-la pela
(delta). Assim,
∆= 𝒃𝟐 − 𝟒𝒂𝒄

23. Fórmula de Bhaskara
Substituindo delta ∆ na fórmula,
encontramos a expressão:
𝒙 =
−𝒃 ± 𝒃𝟐 − 𝟒𝒂𝒄 ∆
𝒙 =
𝟐𝒂
−𝒃 ± ∆
𝟐𝒂
Forma contraída da
Fórmula de Bhaskara.

24. Exemplo 2
Determine o discriminante da equação do
2º grau a seguir:
𝑥2 − 5𝑥 + 6 = 0
𝑎 = 1, 𝑏 = −5, 𝑐 = 6
∆= 𝑏2 − 4𝑎𝑐

25. 𝑥2 − 5𝑥 + 6 = 0 → 𝑎 = 1, 𝑏 = −5, 𝑐 = 6
∆= 𝑏2 − 4𝑎𝑐
∆= −5 2 − 4 ∙ 1 ∙ 6
∆= 25 − 24
∆= 1
Exemplo 2 – Solução

26. Exercício 2
Determine o discriminante da equação do
2º grau a seguir:
3𝑥2 − 2𝑥 − 1 = 0
𝑎 = 3, 𝑏 = −2, 𝑐 = −1
∆= 𝑏2 − 4𝑎𝑐

27. Exercício 2 – Solução
3𝑥2 − 2𝑥 − 1 = 0 → 𝑎 = 3, 𝑏 = −2, 𝑐 = −1
∆= 𝑏2 − 4𝑎𝑐
∆= −2 2 − 4 ∙ 3 ∙ −1
∆= 4 + 12
∆= 16

28. Exercício 3
Determine o discriminante da equação do
2º grau a seguir:
−3𝑥2 + 4𝑥 − 7 = 0
𝑎 = −3, 𝑏 = 4, 𝑐 = −7
∆= 𝑏2 − 4𝑎𝑐

29. 𝑎 = −3
−3𝑥2 + 4𝑥 − 7 = 0 → ቐ 𝑏 = 4
𝑐 = −7
∆= 𝑏2 − 4𝑎𝑐
∆= 42 − 4 ∙ −3 ∙ −7
∆= 16 − 84 →
∆= −68
Exercício 3 – Solução

30. Exercício 4
Resolva a equação do 2º grau a seguir:
3𝑥2 − 2𝑥 − 1 = 0
𝑎 = 3, 𝑏 = −2, 𝑐 = −1
∆= 𝑏2 − 4𝑎𝑐 →
−𝑏 ± ∆
𝑥 =
2𝑎

31. Exercício 4 – Solução
3𝑥2 − 2𝑥 − 1 = 0 → 𝑎 = 3, 𝑏 = −2, 𝑐 = −1
∆= 𝑏2 − 4𝑎𝑐
∆= −2 2 − 4 ∙ 3 ∙ −1
∆= 4 + 12
∆= 16
∆= 16

32. Exercício 4 – Solução
3𝑥2 − 2𝑥 − 1 = 0 → 𝑎 = 3, 𝑏 = −2, 𝑐 = −1
𝑥 =
−𝑏 ± ∆
2𝑎
𝑥 =
− −2 ± 16
2 ∙ 3
∆= 16

33. Exercício 4 – Solução
𝑥 =
− −2 ± 16
2 ∙ 3
2 ± 4
𝑥 =
6

34. Exercício 1 – Solução
𝑥 =
2 ± 4
6
𝑥1 =
2 + 4
6
6
𝑥1 =
6
𝑥1 = 1
2
2 − 4
𝑥 =
6
−2
𝑥2 =
6
1
𝑥2 = −
3
Soluções:
𝑥1 = 1
ou
1
𝑥2 = −
3