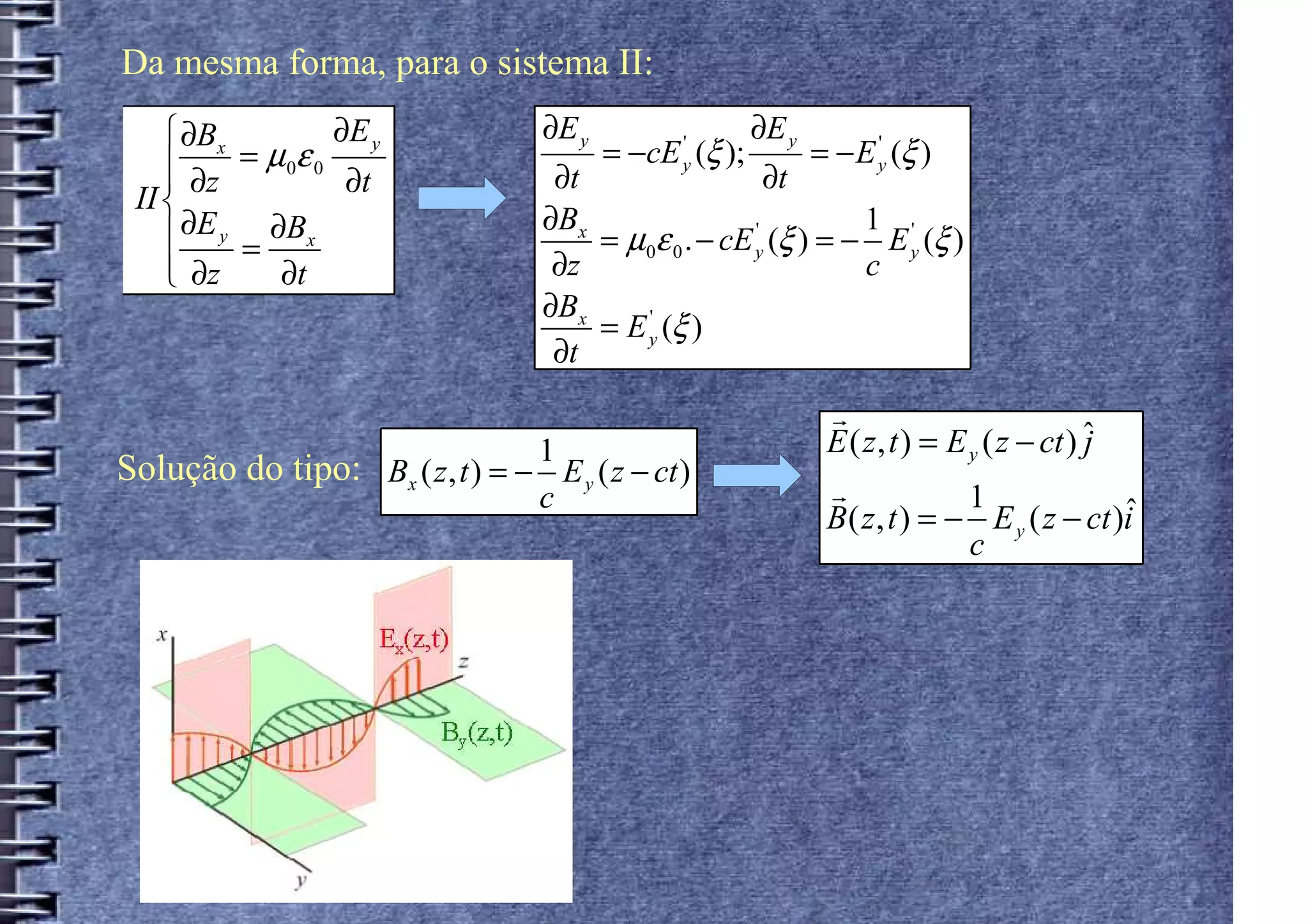
I. O documento descreve as equações de Maxwell no vácuo e sua solução para ondas eletromagnéticas unidimensionais. II. As equações resultam na equação de onda para os campos elétrico e magnético, que se propagam como ondas planas harmônicas ortogonais. III. O campo elétrico e magnético oscilam em fase um com o outro e a uma frequência ω, formando ondas eletromagnéticas que se propagam à velocidade da luz c.

1. A Equação de Onda Eletromagnética
Equações de Maxwell no vácuo, em região sem cargas ou correntes
elétricas: r r
∇ ⋅ E = 0 ⇒ Lei de Gauss para Eletricidade
r r
∇ ⋅ B = 0 ⇒ Lei de Gauss para Magnetismo
r
r r ∂B
∇× E = − ⇒ Lei de Faraday
∂t
r
r r ∂E
∇ × B = ε 0 µ0 ⇒ Lei de Ampère - Maxwell
∂t
r r r r
Solução em uma única dimensão: E = E ( z , t ); B = B ( z , t )
r r ∂E x ∂E y ∂E z ∂E z
∇⋅E = + + =
∂x ∂y ∂z ∂z
r r  ∂E z ∂E y   ∂E x ∂E z   ∂E y ∂E x 
∇× E = 
 ∂y − ∂z i +  ∂z − ∂x  j +  ∂x − ∂y k

ˆ ˆ
 ˆ
     
∂E y
ˆ ∂E j
r r
∇× E = − i+ x ˆ
∂z ∂z

2. r r ∂E z ∂E y ∂B
ˆ + ∂E x ˆ = − ∂Bx i + y ˆ + ∂Bz ˆ
r r
∇.E = =0 ∇× E = − i j 
 ∂t
ˆ j k

∂z ∂z ∂z  ∂t ∂t 
r r ∂Bz ∂E y ∂Bx ∂E x ∂B y ∂Bz
∇.B = =0 ⇒ = ; =− ; =0
∂z ∂z ∂t ∂z ∂t ∂t
∂B y ∂E
ˆ + ∂Bx ˆ = µ 0ε 0  ∂E x i + y ˆ + ∂E z ˆ
r r
∇× B = − i j 
 ∂t
ˆ j k

∂z ∂z  ∂t ∂t 
∂B y ∂E x ∂Bx ∂E y ∂E z
⇒ = − µ 0ε 0 ; = µ 0ε 0 ; =0
∂z ∂t ∂z ∂t ∂t
E z e Bz são constantes ⇒ E z = Bz = 0
 ∂B y ∂E x  ∂Bx ∂E y
 = − µ 0ε 0  = µ 0ε 0
 ∂z ∂t  ∂z ∂t
I II 
 ∂E x = − ∂B y  ∂E y = ∂Bx

 ∂z ∂t  ∂z
 ∂t

3.  ∂B y ∂E  ∂Bx ∂E y
 = − µ 0ε 0 x  = µ 0ε 0
 ∂z ∂t  ∂z ∂t
I II 
 ∂E x = − ∂B y  ∂E y = ∂Bx
 ∂z
 ∂t  ∂z
 ∂t
 ∂ 2 By ∂ 2 Ex
 2 = − µ 0ε 0 (derivada parcial em relação a z)
 ∂z ∂z∂t
I
 ∂ 2 Ex ∂ 2 By
 ∂z∂t = − ∂t 2

(derivada parcial em relação a t)
∂ 2 By ∂ 2 By ∂ 2 By ∂ 2 By
= µ 0ε 0 ⇒ − µ 0ε 0 =0
∂z 2
∂t 2
∂z 2
∂t 2
 ∂ 2 Bx ∂2Ey
 = µ 0ε 0 (derivada parcial em relação a t)
 ∂z∂t ∂t 2
II  2
 ∂ E y ∂ Bx
2
 ∂z 2 = ∂z∂t

(derivada parcial em relação a z)
∂2Ey ∂2Ey ∂2Ey ∂2Ey
= µ 0ε 0 ⇒ − µ 0ε 0 =0
∂z 2
∂t 2
∂z 2
∂t 2

4. ∂ 2 By ∂ 2 By ∂2Ey ∂2Ey
− µ 0ε 0 =0 − µ 0ε 0 =0
∂z 2
∂t 2
∂z 2
∂t 2
∂2 f 1 ∂2 f 1
− 2 2 =0 ; v=
∂z 2
v ∂t µ 0ε 0
Equação de ondas unidimensional
f ( z, t ) = F ( z − vt ) + G ( z + vt )
F → onda caminhante progessiva ( + z)
G → onda caminhante regressiva ( − z)

5. 1
E x ( z , t ) = E x ( z − ct ), v = c =
µ 0ε 0
∂E x dE dE
= −c x = −cE x (ξ ), ξ ≡ z − ct ; E x (ξ ) = x
' '
∂t dξ dξ
∂E x dE x
= = E x (ξ )
'
∂z dξ
 ∂B y ∂E ∂B y 1 '
 = − µ 0ε 0 x = − µ0ε 0 . − cE (ξ ) = E x (ξ )
'
Substituindo no  ∂z ∂t ∂z
x
c
I
sistema I:  ∂E x = − ∂B y ∂B y
= − E x (ξ )
'
 ∂z
 ∂t ∂t
1
Solução do tipo: B y ( z , t ) = E x ( z − ct )
c
r
Onda eletromagnética se propaga na E ( z , t ) = E x ( z − ct )i
ˆ
direção +z, E e B ortogonais entre si r 1
E à direção de propagação: B( z, t ) = E x ( z − ct ) ˆ j
c

6. Da mesma forma, para o sistema II:
 ∂Bx ∂E y ∂E y ∂E y
 = µ 0ε 0 = −cE (ξ );
'
= − E y (ξ )
'
∂t ∂t
y
 ∂z ∂t
II 
∂Bx
 ∂E y = ∂Bx 1 '
= µ0ε 0 . − cE y (ξ ) = − E y (ξ )
'
 ∂z
 ∂t ∂z c
∂Bx
= E y (ξ )
'
∂t
r
1 E ( z , t ) = E y ( z − ct ) ˆ
j
Solução do tipo: Bx ( z , t ) = − E y ( z − ct )
c r 1
B ( z , t ) = − E y ( z − ct )iˆ
c

7. Ondas planas harmônicas
r
E ( z , t ) = Em cos[k ( z − ct ) + δ ]i = Em cos(kz − ωt + δ )i
ˆ ˆ
r
B ( z , t ) = Bm cos(kz − ωt + δ ) ˆ j
Em → amplitude do campo elétrico; Bm → amplitude do campo magnético
ω
k= → número de onda
c
1 2π
T= = → período temporal
f ω
2π
λ= → período espacial ou comprimento de onda
k
E x ( z , t ) = Em cos[k ( z − ct ) + δ1 ] B y ( z , t ) = Bm cos(kz − ωt + δ 2 )
∂E x ∂B y
= − kEm sen(kz − ωt + δ1 ) = ωBm sen(kz − ωt + δ1 )
∂z ∂t
∂E x ∂B y ω 1 1
=− ⇒ kEm = ωBm ⇒ Bm = . Em = .Em
∂z ∂t c ω c