Este documento apresenta um relatório sobre um teste de estatística. Inclui a resolução de vários exercícios estatísticos sobre populações, amostras, variáveis, médias, desvios padrão e correlações. Conclui demonstrando aplicações práticas da estatística no dia a dia.

1. DEPARTAMENTO DE CIÊNCIAS SOCIAIS E HUMANAS
CURSO DE ADMINISTRAÇÃO PÚBLICA
CADEIRA: ESTATÍSTICA
1
o
Ano
Teste 2: Trabalho de Campo
Discente:
Angelina Verssone
Docente:
António Fernando Zucula
Espungabera, Março de 2021.

2. ÍNDICE
Introdução..................................................................................................................................................................................1
Resolução De Exercícios.....................................................................................................................................................2
Conclusão..................................................................................................................................................................................8
Referências Bibliográficas..................................................................................................................................................9

3. INTRODUÇÃO
Inicialmente, a actividade estatística surgiu como um ramo da Matemática. Limitava-se ao estudo
de medições e técnicas de contagem de fenómenos naturais e ao cálculo de probabilidades de
acontecimentos que se podiam repetir indefinidamente. Actualmente, os métodos estatísticos são
utilizados em muitos sectores de actividade, tendo como algumas aplicações estudos de
fiabilidade, pesquisas de mercado, testes de controlo de qualidade, tratamento de inquéritos,
sondagens, modelos econométricos, previsões.
Portanto, neste trabalho buscamos mostrar como a estatística se pode usar de uma maneira prática
na resolução dos problemas que deparamos com eles no nosso quotidiano, com base na resolução
de alguns problemas práticos.
1

4. RESOLUÇÃO DE EXERCÍCIOS
1. População é um conjunto de indivíduos ou objectos que apresentam pelo menos uma
característica em comum. Ao passo que amostra refere-se a todo o subconjunto não vazio e
com menor número de elementos do que o conjunto definido como população.
2. Variável independente: é aquela que muda ou é controlada para ver os seus efeitos na
variável dependente, matematicamente falando, eles são os elementos de entrada da equação
ou modelo de estudo, enquanto Variável dependente: é aquela que é afectada pela variável
independente, sendo assim considerado de saídas de um modelo ou de uma equação.
Exemplos: Estou realizando tarefas para ganhar mesada. E para cada tarefa, que eu realizo, ganho
$3
 Variável independente: A variável independente é a quantidade de tarefas que eu faço,
pois essa é a variável sobre a qual tenho controlo.

 Variável dependente: A variável dependente é a quantia do dinheiro que ganho, pois ela
depende de quantas tarefas realizei.



3. Para responder a esta questão, primeiro temos de saber o tempo médio que o professor gasta de
casa para o local de serviço, calculando assim a média aritmética para cada transporte no
período em descrição.
Chapa 100: 28 29 32 37 33 25 29 32 41 34
Transporte público: 29 31 33 32 34 30 31 32 35 33
chapa 100 =
28+29+32+37+33+25+29+32+41+34
=
320
= 32
10 10
29+31 +33+32+34+30+31+32+35+33 320
.= 10 = 10 = 32
R.: Ambos os transportes. Porque tanto usando o chapa 100, assim como o transporte público, o
professor gasta em média 32 minutos para chegar ao local de trabalho.
2

5. 4.
Remuneração Fi fi Fi xi hi fi/hi xi.fi (Xi- )2
fi. (Xi- )2
(%) (%)
[60; 80[ 7,8 0,078 7,8 70 20 0,0039 5,46 29 787,3081 2 323,4100318
[80; 100[ 15,2 0,152 23 90 20 0,0076 13,68 23 283,7081 3 539,1236312
[100; 120[ 31,2 0,312 54,2 110 20 0,0156 34,32 17 580,1081 5 484,9937272
[120; 140[ 19,5 0,195 73.7 130 20 0,00975 25,35 12 676,5081 2 471,9190795
[140; 160[ 7,2 0,072 80.9 150 20 0,0036 10,8 8 572,9081 617,2493832
[160; 200[ 8,1 0,081 89 180 40 0,00202 14,58 3 917,5081 317,3181561
[200; 250[ 5,4 0,054 94,4 225 50 0.00108 121,5 309,4081 16,7080374
[250; 300[ 2,6 0,026 97 275 50 0,00052 7,15 1 050,4081 27,3106106
[300; 350[ 3 0,03 100 325 50 0,0006 9,75 6 791,4081 203,742243
Total 100 1 242, 59 86 858,4729 14 804,14492429
a) Dados: Fórmula/Resolução
L(máx.) = 350 AT= L(max)-L(min)
L(min.) = 60 AT= 350-60
AT =? AT= 290.
R.: A amplitude total da distribuição dos empregados desta instituição é igual a 290.
b) = ∑ ∙!
(70 × 7,8%) + (90 × 15,2%) + (110 × 31,2%) + (130 × 19,5%) + (150 × 7,2%) + (180 × 8,1%) 100%
(225 × 5,4%) + (275 × 2,6%) + (325 × 3%)
. .
3

6. =
24259%
= 242, 59
100%
A media aritmética da distribuição é igual a 242, 59.
 A classe modal é aquela a que corresponde maior frequência por unidade de amplitude.
Neste caso, o maior valor de fi/hi é 0,0156 correspondente à classe [100; 120 [.
1. Variância:
Dados
(Xi − X) . i = . 0 , . / 3 3
N= 100%
Fórmula/Resolução
= ∑(Xi − X) . i = .0,./3 = 148,0414492429 ≈ 148,04.
n 100
R: A variância da distribuição é aproximadamente igual a 148, 04.
Desvio Padrão:
Dados
S
2
= 148, 04
Fórmula/Resolução
= = 148,04 = , 9.
R: O desvio Padrão da distribuição é igual a 12, 167.
4

7. 2. Fórmula:
(<− @−)
; ==+ ∙
( )
 Classe a que pertence Q1 (classe a que corresponde uma frequência acumulada 0,25):
[100; 120[
1=100+
(0,25 − 0,23)
×20=> 1=100+
0,2 × 20
=> 1 = 101, 23.
0,312 0,312
R: O valor correspondente a quartil um (Q1) é 101, 23.
 Classe a que pertence Q2 (classe a que corresponde uma frequência acumulada 0,5):
[100; 120[
2=100+
(0,5 − 0,23)
×20=> 2=100+
0,27 × 20
=> 2 = 117, 3.
0,312 0,312
R: O quartil dois (Q2) é igual a 117, 3.
 Classe a que pertence Q3 (classe a que corresponde uma frequência acumulada 0,75):
[140; 160[
3=140+ (0,75 − 0,737)
×20=> 3=140+ 0,013 × 20
=> 3 = 143, 61.
0,072 0,072
R: O valor de quartil três corresponde a 143, 61 na distribuição.
3. Dados
S= , 9
= 242, 59
Fórmula/Resolução
E = ×100 => E =
12, 167
× 100 => E = 0,05 × 100 = 5%.
242, 59
R: O coeficiente de variação desta distribuição é igual a 0,05, que corresponde a 5%.
5

8. 5. Dados Fórmula:
Pão forma (A): 9,8% P(A) = ú K L O P R S á L
ú J M P R W Rí L
Pão Arrufado (B): 22,9%
Ambos tipos de pães (C): 5,1%
a) P(A)+P(B)+P(C)
9,8% 22,9% 5,1%
( ) + ( ) +
( )=100% +
100% +
100%
( ) + ( ) + ( ) = 0,098 +0,229 +0,051 =0,378.
R: A probabilidade de pessoa comprar pelo menos um dos dois tipos de pães é de 0,378 ou seja,
37,8%.
b) P(A) = úJ M O P Q T á L = , % = 0,098
ú K L O P R RíX L %
R: A probabilidade de uma pessoa comprar pão forma é de 0,098.
6

9. 6.
Lote Volume (unidades Custo (Mtn)
Custo (Mtn)
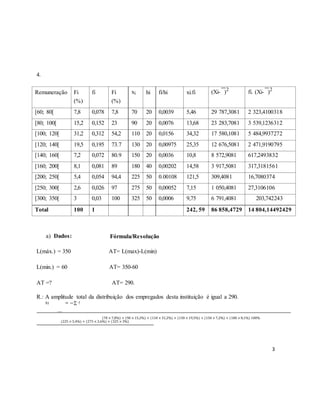
1 1500 3100
2 800 1900
6000
3 2600 4200
4 1000 2300 5000
5 600 1200
6 2800 4900 4000
7 1200 2800
3000
8 900 2100
Custo (Mtn)
9 400 1400
2000
10 1300 2400
11 1200 2400
1000
12 2000 3800
0
0 1000 2000 3000
b) A correlação existente entre volume e custo de produção é positiva quase perfeita.
c) r =
` [( h , )( h j , ) ⋯ ( , ^ g, )( h j , )]
√ a ` = √ , ^ ×√ n g
r =√ `
a
= 0,98.
`
R: O coeficiente de correlação é igual a 0,98.
7

10. CONCLUSÃO
Em nosso dia a dia, frequentemente estamos fazendo observações de fenô- menos e gerando
dados. Os professores analisam dados de alunos; analistas de sistemas analisam dados de
desempenho de sistemas computacionais; médicos analisam resposta do paciente a tratamentos, e
todos nós, ao lermos jornais e revistas, estamos vendo resultados estatísticos provenientes do
censo demográfico, de pesquisas eleitorais, da bolsa de valores.
Estatística é um campo do estudo centrado na produção de metodologia para coleta, organização,
descrição, análise e interpretação de dados bem como na obtenção de conclusões válidas e na
tomada de decisões razoáveis baseadas em tais análises.
Por conseguinte, as duas premissas acima citada, fizeram-se sentir a medida que fui resolvendo os
exercícos e ver como a estística oferece métodos tão simples e práticos, embora probabilísticos de
resolução de problemas.
8

11. REFERÊNCIAS BIBLIOGRÁFICAS
ISCED, Estatística-Manual do curso de Administração Pública, s.e, Beira, 2019.
POCINHO, Margarida, Estatística volume I, Rio de Janneiro, 2009.
ESPAÇO ANTLÂNTICO, Manual técnico do formando-Estatística Aplicada, Lisboa, s.a
MEASURE EVALUATION, Módulo II-Noções de Estatística Básica, Maputo, 2008.
ALMEIDA, Rosa Lívia Freitas, et all, Matemática-Estatística e probabilidade, 3a
edição,
Fortaleza-Ceará, São Paulo, 2015.
9