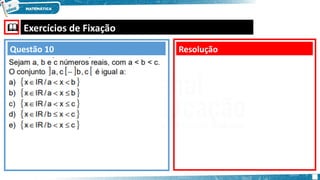
O documento aborda a teoria dos conjuntos, explicando definições, denotações, representações, diagramas de Venn, relações de pertinência, igualdade e desigualdade de conjuntos, e conceitos como subconjuntos, união, intersecção e conjunto vazio. São apresentados exemplos práticos e exercícios de fixação para facilitar a compreensão dos conceitos. Além disso, o documento menciona conjuntos numéricos, incluindo naturais, inteiros, racionais, irracionais e reais, detalhando suas definições e subconjuntos.







































![ Intervalos Reais
Intervalo Aberto
Por descrição: {x IR | a < x < b}
Por notação: ]a, b[
Na reta real:
Intervalo Fechado
Por descrição: {x IR | a x b}
Por notação: [a, b]
Na reta real:
Intervalo aberto à esquerda e fechado
à direita
Por descrição: {x IR | a < x b}
Por notação: ]a, b]
Na reta real:
Intervalo fechado à esquerda e
aberto à direita
Por descrição: {x IR | a x < b}
Por notação: [a, b[
Na reta real:](https://image.slidesharecdn.com/387991fc35fb9dc60bb8d40e010bbc136cd44-240708132239-14e7f0a5/85/38799_1fc35fb9dc60bb8d40e010bbc136cd44-pdf-50-320.jpg)
![ Intervalos Reais
Intervalo fechado em a
Por descrição: {x IR | x a}
Por notação: [a, + [
Na reta real:
Intervalo aberto em a
Por descrição: {x IR | x > a}
Por notação: ]a, + [
Na reta real:
Intervalo fechado em b
Por descrição: {x IR | x b}
Por notação: ]- , b]
Na reta real:
Intervalo aberto em b
Por descrição: {x IR | x < b}
Por notação: ]- , b[
Na reta real:](https://image.slidesharecdn.com/387991fc35fb9dc60bb8d40e010bbc136cd44-240708132239-14e7f0a5/85/38799_1fc35fb9dc60bb8d40e010bbc136cd44-pdf-51-320.jpg)
![ Exercícios de Fixação
Sejam os intervalos:
A = ]− ∞ 1,] B = ]0, 2 ] C = [ − 1,1 ]
O intervalo C (A ∩ B) é:
∪
a) ]− 1,1 ]
b) [ − 1,1 ]
c) [ 1,0 ]
d) ] 1,0 ]
Resolução
Questão 03](https://image.slidesharecdn.com/387991fc35fb9dc60bb8d40e010bbc136cd44-240708132239-14e7f0a5/85/38799_1fc35fb9dc60bb8d40e010bbc136cd44-pdf-54-320.jpg)