1) O documento discute escalares e vetores, apresentando exemplos de grandezas escalares e vetoriais.
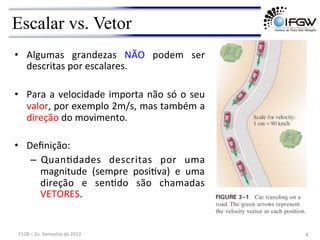
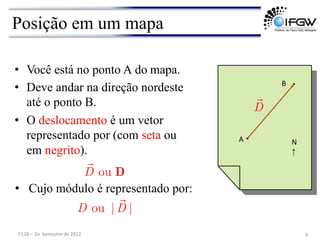
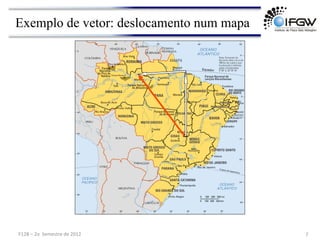
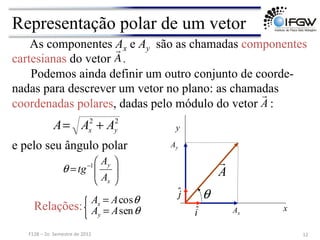
2) É explicado que vetores, ao contrário de escalares, requerem a especificação de magnitude, direção e sentido para serem completamente descritos.
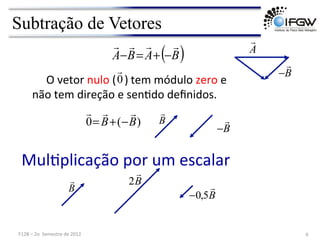
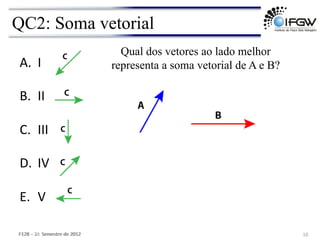
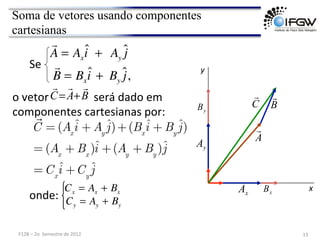
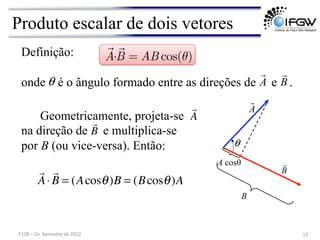
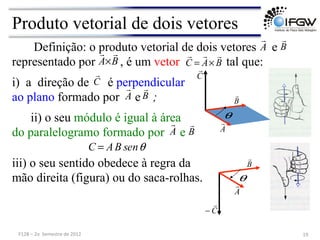
3) São apresentadas operações com vetores como soma, subtração, multiplicação por escalar e produto escalar e vetorial.