Programação linear
- 1. Escola Secundaria Ferreira Dias Professoera de Matemática Programação Linear Na disciplina de: Matemática Professora: Cristina Correia Na turma: 10ºT Feito por: Carina Silva nº7 Cátia Ribeiro nº8 Jessica Gonçalves nº16 Zulmaria Loupa nº27 1 1ºT Carina Silva nº7 Cátia Ribeiro nº8 Jessica Gonçalves nº16 Zulmira Loupa nº27
- 2. Escola Secundaria Ferreira Dias Professoera de Matemática Indice Introdução O que é a programação linear? Para que serve? Onde se aplicam os seus conhecimentos? Exemplos de P.L Conclusão 2 1ºT Carina Silva nº7 Cátia Ribeiro nº8 Jessica Gonçalves nº16 Zulmira Loupa nº27
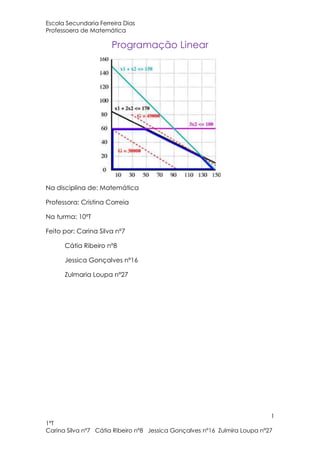
- 3. Escola Secundaria Ferreira Dias Professoera de Matemática O que é programação linear? Através desta ferramenta consegue-se encontrar a solução óptica para certos tipos de problemas, tem sido apliacada por diversas entidades e empresas a inúmeros problemas. Entre os primeiros estudos não militares a serem concluídos, destaca-se amultinacional de restauração McDonald's, estudou a optimização dos horários detrabalho em quatro estabelecimentos e conseguiu uma mais eficiente utilização damão-de-obra, em grande parte a tempo parcial, e com maior grau de satisfação porparte dos trabalhadores. Para que serve a programação linear? A programação linear serve para resolver problemas onde todas as suas variáveis são restritas a números inteiros. Onde se aplicam os seus conhecimentos? É aplicada por diversas entidades e empresas a inúmeros problemas. Exemplos de PL Uma empresa fabrica dois produtos A e B. Cada um deste produtos requer umacerta quantidade de tempo na linha de montagem e ainda mais algum para a sua finalização. Cada produto do tipo A necessita de 5 horas na linha de montagem e de 2 horas para a finalização. Cada produto de tipo B necessita de 3 horas na linha de montagem e de 4 horas para a finalização. Numa semana, a empresa dispõe de 108 horas para a linha de montagem e 60 horas para a finalização. Toda a produção é vendida. O lucro de cada produto é de 120 € para o produto A e de 210 € para o B. Quantas unidades, por semana, dos produtos A e B se devem produzir, de modo a que o lucro seja máximo? Podemos elaborar uma tabela para melhor esquematizar os dados: A B Disponibilidade Montagem 5 3 180 Finalização 2 4 60 Lucro 120 210 3 1ºT Carina Silva nº7 Cátia Ribeiro nº8 Jessica Gonçalves nº16 Zulmira Loupa nº27
- 4. Escola Secundaria Ferreira Dias Professoera de Matemática Seja x o número de unidades que a empresa produz, por semana, do produto A e y o número de unidades que a empresa produz, por semana, do produto B. O tempo necessário na linha de montagem para os dois produtos é 5x+3y horas, no total. Como somente existem 108 horas de disponibilidade, temos a restrição: 5x+3y ≤ 108 De forma análoga temos a seguinte restrição: 2x+4y ≤ 60 4 1ºT Carina Silva nº7 Cátia Ribeiro nº8 Jessica Gonçalves nº16 Zulmira Loupa nº27
