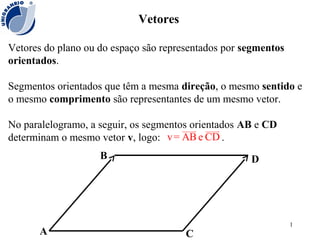
1. 1
Vetores
Vetores do plano ou do espaço são representados por segmentos
orientados.
Segmentos orientados que têm a mesma direção, o mesmo sentido e
o mesmo comprimento são representantes de um mesmo vetor.
No paralelogramo, a seguir, os segmentos orientados AB e CD
determinam o mesmo vetor v, logo: .v= AB e CD
uuuur uuuur
A
B
C
D

2. 2
Quando escrevemos , estamos afirmando que o vetor é
determinado pelo segmento orientado AB de origem A e extremidade
B.
Qualquer outro segmento de mesmo comprimento, mesma direção e
mesmo sentido de AB representa também o vetor v.
Cada ponto do espaço pode ser considerado como origem de um
segmento orientado que é representado por v.
O comprimento ou o módulo, a direção e o sentido de um vetor v é,
também, o módulo, a direção e o sentido de qualquer um de seus
representantes.
O módulo de v é indicado por .
v= AB
uuuur
v

3. 3
Todo ponto do espaço representa o vetor zero, também chamado de
vetor nulo, e é indicado por 0.
A cada vetor não nulo v corresponde um vetor oposto –v, que tem o
mesmo módulo, a mesma direção e sentido contrário ao de v.
Um vetor v é unitário se .
v
.-v
v 1=

4. 4
Dois vetores u e v são colineares se tiverem a mesma direção.
u e v são colineares se tiverem representantes AB e CD pertencentes
a uma mesma reta ou a retas paralelas.
.
B
.A v
CD
.u
. .A Bv C Du

5. 5
Os vetores não nulos u, v e w ( o número de vetores não importa)
possuem representantes AB, CD e EF pertencentes a um mesmo
plano , diz-se que eles são coplanares.
.
B
.A u
C
D
.v
.
E
F
wπ
π

6. 6
Operações com vetores
Adição de vetores: Sejam os vetores u e v representados pelos
segmentos orientados AB e BC, respectivamente:
Os pontos A e C determinam o vetor soma .AC = u + v
uuuur
A
B
C
u v
u + v

7. 7
Operações com vetores
Propriedades da adição:
i) Associativa: (u + v) + w = u + (v + w).
ii) Comutativa: u + v = v + u.
iii) Existe somente um vetor nulo 0 tal que, para todo vetor v, se tem:
v + 0 = 0 + v = v
iv) Qualquer que seja o vetor v, existe somente o vetor –v , chamado
de oposto de v, tal que:
v + (-v) = -v + v = 0 .

8. 8
A
B
C
D
u + v
v + u
u
u
v
v

9. 9
A
B
C
D
u
-v
v
-u
A
B
C
D
u
v
- v
u
u
-u
v
v

10. 10
Operações com vetores
Multiplicação de um Número Real por um Vetor: Dado um vetor v
(diferente de zero) e um número real k (diferente de zero), chama-se
produto do número real k pelo vetor v o vetor u = kv, tal que:
a) módulo: .
b) direção: a mesma de v.
c) sentido: se k > 0 o mesmo de v; e contrário ao de v se k < 0.
u kv k v= =
.
.
v
2v
.- 3v

11. 11
Operações com vetores
Propriedades da Multiplicação por um Número Real:
i) a(bu) = (ab)u.
ii) (a + b)u = au + bu.
iii) a(u + v) = au + av.
iv) 1u = u.

12. 12
Vetores
O paralelogramo ABCD é determinado pelos vetores ,
sendo M e N pontos médios dos lados DC e AB, respectivamente.
Calcule:
AB e CD
uuuur uuuur
A
D
B
C
a) AD + AB b) BA + DA c) AC - BC
1d) AN + BC e) MD + MB f) BM - DC
2
uuuuv uuuuv uuuuv uuuuuv uuuuv uuuuv
uuuuv uuuuv uuuuvuuuuuv uuuuuv uuuuuv
M
N
.
.

13. 13
Vetores
.
A
D
B
C
=a) AD + AB AC
uuuuv uuuuv uuuuv
M
N
.
.

14. 14
Vetores
.
A
D
B
C
M
N
.
.
= + =b) BA + DA CD DA CA
uuuuv uuuuuv uuuuv uuuuuv uuuuv

15. 15
Vetores
. = =c) AC - BC AC + CB AB
uuuuv uuuuv uuuuv uuuuv uuuuv
D
B
C
N
.
.
M
A

16. 16
Vetores
. = =d) AN + BC AN + NM NB + NM AMou NC=
uuuuruuuuv uuuuv uuuuv uuuuuvuuuuuv uuuuv uuuuuv
D
B
C
N
.
.
M
A

17. 17
Vetores
. = =e) MD + MB MD + DN MN
uuuuuv uuuuuv uuuuuv uuuuuv uuuuuv
D
B
C
N
.
.
M
A

18. 18
Vetores
. = =1f) BM - .DC BM + MD BD
2
uuuuvuuuuuv uuuuuv uuuuuv uuuuv
D
B
C
N
.
.
M
A

19. 19
Ângulo de Dois Vetores
.
u
O ângulo de dois vetores u e v não nulos é o ângulo formado pelas
semirretas OA e OB e tal que 0 .
θ
θ π≤ ≤
ur ur
v
0
A
B
θ

20. 20
Ângulo de Dois Vetores
.u v
0
θ=π
a) Se , u e v têm a mesma direção e sentidos con= trários.θ π
ur ur
b) Se , u e v têm a mesma direção e o mesmo= 0 sentido.θ
ur ur
. u v0
θ=0

21. 21
Ângulo de Dois Vetores
.
u
v0
.c) Se , u e v são ortogonais e indica-se:u v=
2
πθ ⊥
ur ur ur ur
v
uu + v
.
A
B
C
2 2 2
O ΔOBC permite escrever: .u+v = u + v

22. 22
Ângulo de Dois Vetores
.d) O vetor nulo é considerado ortogonal a qualquer vetor
e) Se u é ortogonal a v e k R , u é ortogonal a kv.∈
urr r r
.
f) O ângulo formado pelos vetores u e -v é o suplemento do ângulo
de u e v
ur ur
ur ur
.-v v
θπ −
θ
u

23. 23
. v60º
u
Sabendo que o ângulo entre os vetores u e v é de 60º,
determinar o ângulo formado pelos vetores:
a) u e -v
b) -u e v
c) -u e -v
d) 2u e 3v
uv uv
uv uv
uv uv
uv uv
uv uv

24. 24
.-v v
u
a) u e -v
uv uv
120º
60º

25. 25
. v
u
b) -u e v
uv uv
60º
-u 120º

26. 26
.-v v
-u
c) -u e -v
uv uv
60º
60º
u

27. 27
. 3v
2u
d) 2u e 3v
uv uv
60º