Unidade 3 cap 1.2 (b) e cap 1.3

Validade de um argumento:
validade formal = depende exclusivamente da sua forma
ou
validade informal = depende também do seu conteúdo proposicional
Forma argumentativa
= a estrutura do argumento
(sem qualquer referência ao seu conteúdo proposicional)
Inspetor de circunstâncias
= dispositivo gráfico
sucessão de tabelas de verdade (para cada premissa e para a conclusão)
que permite determinar se uma forma argumentativa é válida
(obs: aplicável apenas à determinação da validade formal)

Ex. 1
Matosinhos é uma cidade do norte e do interior de Portugal (F)
Portanto, Matosinhos é uma cidade do interior de Portugal (F)
Interpretação: P = Matosinhos é uma cidade do norte de Portugal.
Q = Matosinhos é uma cidade do interior de Portugal
P ∧ Q
Q
P Q P ∧ Q ╞ Q
V V V V
V F F F
F V F V
F F F F
Tabela de verdade da
premissa
Martelo semântico
(“logo” ou “portanto”)
Tabela de verdade da
conclusão
O argumento é [dedutivamente] válido porque em nenhuma circunstância
a premissa é verdadeira e a conclusão falsa (isso é impossível)

Ex. 2
Matosinhos é uma cidade do norte ou do interior de Portugal (V)
Portanto, Matosinhos é uma cidade do norte de Portugal (V)
Interpretação: P = Matosinhos é uma cidade do norte de Portugal.
Q = Matosinhos é uma cidade do interior de Portugal
P ∨ Q
P
P Q P ∨ Q ╞ P
V V V V
V F V V
F V V F
F F F F
O argumento é [dedutivamente] inválido porque há uma circunstância
em que a premissa é verdadeira e a conclusão falsa (isso é possível)

OBS:
Um argumento não é válido numas circunstâncias e inválido noutras
Se em alguma circunstância a premissa é verdadeira e a conclusão é falsa,
isto é,
se é possível o argumento ter premissa(s) verdadeira(s) e conclusão falsa,
então
o argumento é [dedutivamente] inválido
O inspetor de circunstâncias também torna evidente
que:
1 – sendo as premissas verdadeiras
2 – sendo o argumento válido
3 – é impossível (sabendo 1 e 2) rejeitar a conclusão

Coerência
Argumento coerente = aquele em que é possível a(s) premissa(s) e a conclusão
serem verdadeiras simultaneamente.
(independentemente da validade)
Esta forma argumentativa é inválida (ver 2.ª linha) mas coerente (ver 1.ª linha)
P Q P ∨ Q ╞ Q
V V V V
V F V F
F V V V
F F F F

P P ╞ P
V V F
F F V
P Q P ∧ Q ╞ Q
V V V V
V F F F
F V F V
F F F F
Lisboa fica em Espanha.
Logo, Lisboa não fica em Espanha
Espanha é um país europeu e ibérico.
Logo Espanha é um país ibérico
Esta forma argumentativa é
inválida (ver 1.ª linha) e incoerente.
Esta forma argumentativa é válida
e coerente (ver 1.ª linha)
Interpretação:
P = Lisboa fica em Espanha
Interpretação:
P = Espanha é um país europeu.
Q = Espanha é um país ibérico.

Avaliação dos argumentos
“No domingo {quase que de certeza absoluta que} não saio porque {,eu já sei como é
nestas situações, eu} estudo, e {o caso, como de costume, põe-se nestes termos: ou}
saio ou {então} estudo.”
1.º
Colocar o argumento na forma canónica:
No domingo saio ou estudo
No domingo estudo
Logo, no domingo não saio
2.º
Fazer a interpretação:
P = No domingo saio
Q = No domingo estudo

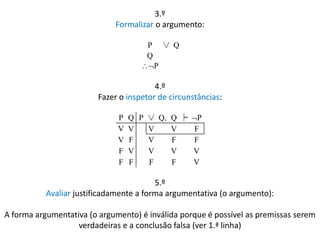
3.º
Formalizar o argumento:
P ∨ Q
Q
P
4.º
Fazer o inspetor de circunstâncias:
P Q P ∨ Q, Q ╞ P
V V V V F
V F V F F
F V V V V
F F F F V
5.º
Avaliar justificadamente a forma argumentativa (o argumento):
A forma argumentativa (o argumento) é inválida porque é possível as premissas serem
verdadeiras e a conclusão falsa (ver 1.ª linha)

Argumentos (e formas argumentativas) válidos e inválidos
Alguns argumentos (e respetivas formas argumentativas)
válidos e falaciosos
por serem muito comuns têm designações próprias.
1.1 – Modus Ponens
1.2 – Modus Tollens
1.3 – Falácia do Modus Ponens
1.4 – Falácia do Modus Tollens
2.1 – Silogismo Disjuntivo
2.2 – Falácia do Silogismo Disjuntivo
3 – Silogismo Hipotético
Falácia = argumento que, por exemplo, parece válido mas não é.

1.1
Modus Ponens
(modo que afirma)
Se o individuo é português, então é europeu.
O individuo é português.
Logo, o individuo é europeu.
Interpretação: P = O individuo é português. Q = O individuo é europeu.
P  Q
P
Q
P Q P  Q, P ╞ Q
V V V V V
V F F V F
F V V F V
F F V F F
Regra:
Na 2.ª premissa afirma-se o antecedente, na conclusão afirma-se o consequente.

1.2
Modus Tollens
(modo que nega)
O individuo não é europeu.
Logo, o individuo não é português.
P  Q
Q
P
P Q P  Q, Q ╞ P
V V V F F
V F F V F
F V V F V
F F V V V
Regra:
Na 2.ª premissa nega-se o consequente, na conclusão nega-se o antecedente.

1.3
Falácia da Afirmação do Consequente (Falácia do Modus Ponens)
O individuo é europeu.
Logo, o individuo é português.
P  Q
Q
P
P Q P  Q, Q ╞ P
V V V V V
V F F F V
F V V V F
F F V F F
Falácia:
Na 2.ª premissa afirma-se o consequente, na conclusão afirma-se antecedente.

1.4
Falácia da Negação do Antecedente (Falácia do Modus Tollens)
O individuo não é português.
Logo, o individuo não é europeu.
P  Q
P
Q
P Q P  Q, P ╞  Q
V V V F F
V F F F V
F V V V F
F F V V V
Falácia:
Na 2.ª premissa nega-se o antecedente, na conclusão nega-se o consequente.

2.1
Silogismo Disjuntivo
O FCP equipa de vermelho ou de azul.
O FCP não equipa de vermelho.
Logo, o FCP equipa de azul.
Interpretação: P = O FCP equipa de vermelho. Q = O FCP equipa de azul.
P ∨ Q
P
Q
P Q P ∨ Q, P ╞ Q
V V V F V
V F V F F
F V V V V
F F F V F
Regra:
Na 2.ª premissa nega-se uma das disjuntas, na conclusão afirma-se a outra.

2.2
Falácia da Afirmação da Disjunta (Falácia do Silogismo Disjuntivo) {extra programa}
O Homem é determinado ou tem livre-arbítrio.
O Homem é determinado.
Logo, o Homem não tem livre-arbítrio.
Interpretação: P = O Homem é determinado. Q = O Homem tem livre-arbítrio.
P ∨ Q
P
Q
P Q P ∨ Q, P ╞ Q
V V V V F
V F V V V
F V V F F
F F F F V
Falácia:
Na 2.ª premissa afirma-se uma das disjuntas, na conclusão nega-se a outra.

3
Silogismo Hipotético
Se o animal é primata, então é mamífero .
Se o animal é mamífero, então é vertebrado.
Logo, se o animal é primata, então é vertebrado.
Interpretação: P = O animal é primata. Q = O animal é mamífero.
R = O animal é vertebrado
P  Q
Q  R
P  R

P  Q
Q  R
P  R
P Q R P  Q, Q  R ╞ P  R
V V V V V V
V V F V F F
V F V F V V
V F F F V F
F V V V V V
F V F V F V
F F V V V V
F F F V V V
Regra:
Na conclusão o antecedente da 1.ª premissa implica o consequente da última.

As equivalências podem funcionar como regras
de substituição
(de uma das equivalentes pela outra
porque têm o mesmo valor de verdade em todas as circunstâncias)
ou
de inferência válida
(cada uma das equivalentes pode ser inferida da outra)
4 – Contraposição
5.1 – Leis de De Morgan: Negação da Conjunção
5.2 – Leis de De Morgan: Negação da Disjunção
6 – Negação da Condicional

4
Contraposição
Se o cidadão é leceiro, então é matosinhense.
Equivale a:
Se o cidadão não é matosinhense, então não é leceiro.
Interpretação: P = O cidadão é leceiro. Q = O cidadão é matosinhense.
(P  Q)  (Q  P)
P Q P  Q Q  P
V V V F V F
V F F V F F
F V V F V V
F F V V V V
Regra:
Inverte-se a posição dos antecedente/consequente e a afirmação/negação.

5.1
Leis de De Morgan: Negação da Conjunção
É falso que Bragança seja uma cidade costeira e do Norte.
Equivale a:
Bragança não é uma cidade costeira ou não é uma cidade do Norte.
Interpretação: P = Bragança é uma cidade costeira.
Q = Bragança é uma cidade do Norte.
 (P ∧ Q)  (P ∨ Q)
P Q  (P ∧ Q) P ∨ Q
V V F V F F F
V F V F F V V
F V V F V V F
F F V F V V V
Regra:
A negação da conjunção equivale à negação das disjuntas .

5.2
Leis de De Morgan: Negação da Disjunção
É falso que Matosinhos seja uma cidade espanhola ou francesa.
Equivale a:
Matosinhos não é uma cidade espanhola nem (e não) é uma cidade francesa.
Interpretação: P = Matosinhos é uma cidade espanhola.
Q = Matosinhos é uma cidade francesa.
 (P ∨ Q)  (P ∧ Q)
P Q  (P ∨ Q) P ∧ Q
V V F V F F F
V F F V F F V
F V F V V F F
F F V F V V V
Regra:
A negação da disjunção equivale à negação das conjuntas .

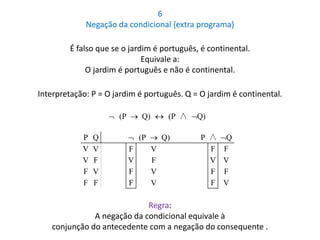
6
Negação da condicional {extra programa}
É falso que se o jardim é português, é continental.
Equivale a:
O jardim é português e não é continental.
Interpretação: P = O jardim é português. Q = O jardim é continental.
 (P  Q)  (P ∧ Q)
P Q  (P  Q) P ∧ Q
V V F V F F
V F V F V V
F V F V F F
F F F V F V
Regra:
A negação da condicional equivale à
conjunção do antecedente com a negação do consequente .

Regras de Inferência ou Leis Lógicas
Nas formas argumentativas surgem variáveis proposicionais (P, Q, R, ...)
1
P  Q
Q
P
3
2 4
P  (Q ∧ R)
 (Q ∧ R)
P
(P ∧ Q)   (R ∨ S)
R ∨ S
  (P ∧ Q)
 (P ∨ Q)  R
R
P ∨ Q
Estas 4 formas argumentativas são na realidade 4 instâncias do Modus Tollens

As diversas instâncias, por exemplo, do Modus Tollens
podem ser representadas numa única fórmula,
utilizando variáveis de fórmula (A, B, C, ...)
A  B
B
A
“A” representa qualquer antecedente e “B” representa qualquer consequente
(proposições simples ou compostas indiferentemente)
As fórmulas são regras ou leis lógicas
(padrões ou modelos a partir dos quais se constroem argumentos válidos)

Validade Dedutiva Informal
Alguns argumentos são [dedutivamente] válidos não devido à sua forma
mas por causa do seu conteúdo proposicional (informalmente)
Validade Semântica
(depende do significado
dos termos envolvidos)
Validade Conceptual
(depende da relação
entre os conceitos envolvidos)
Cinco é um número ímpar.
Logo, cinco não é um número par.
O céu é azul.
Logo o céu tem cor.
“Ímpar” e “par” são termos
antónimos.
O conceito de “azul” integra o
conceito de “cor”.

Interpretação:
P = Cinco é um número ímpar.
Q = Cinco é um número par.
Interpretação:
P = O céu é azul.
Q = O céu tem cor.
P
Q
P
Q
P Q P ╞ Q
V V V F
V F V V
F V F F
F F F V
P Q P ╞ Q
V V V V
V F V F
F V F V
F F F F
Ambos os argumentos são formalmente inválidos
mas informalmente [dedutivamente] válidos
O inspetor de circunstâncias apenas deteta a validade formal

Unidade 3 cap 1.2 (b) e cap 1.3

Mais conteúdo relacionado

Mais procurados

Semelhante a Unidade 3 cap 1.2 (b) e cap 1.3

Último

Unidade 3 cap 1.2 (b) e cap 1.3