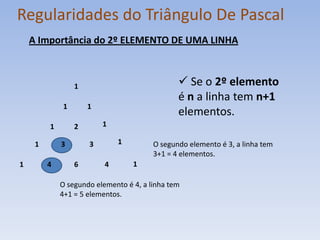
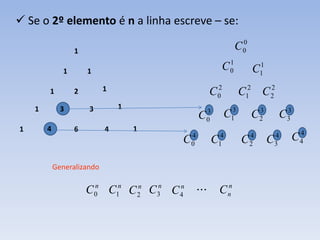
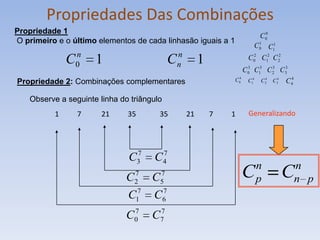
O documento apresenta as propriedades do triângulo de Pascal, incluindo: 1) como construir o triângulo de Pascal; 2) que cada elemento pode ser escrito como uma combinação; 3) as regularidades do triângulo como a relação entre o segundo elemento de uma linha e o número de elementos da linha.

1. Probabilidades e
Combinatórias
12 º Ano

2. Um pouco da História…
O triângulo de Pascal ou de Tartaglia é um
triângulo aritmético, formado por números
que se relacionam entre si. Blaise Pascal
Muitas das relações existentes
entre estes números foram
descobertas por Tartaglia (1500– Sabe-se hoje que o triângulo com
1557). Posteriormente, Blaise estas propriedades já era conhecido
do matemático chinês Yang Hui
Pascal (1623–1662) também se
(século XIII) e que terá sido o
ocupou do estudo exaustivo matemático Omar Khayyam (1048 –
deste triângulo, motivo pelo qual 1122) o primeiro a descobrir o
se atribui o nome destes dois triângulo.
matemáticos.

3. Como Construir o triângulo de Pascal?
• A primeira linha é o número 1. 1
1 1
• A linha seguinte tem sempre +
mais um número que a anterior e 1 2 1
todas as linhas começam e + +
acabam em 1. 1 3 3 1
1 4 6 4 1
• Cada termo de uma linha
(exceto os extremos) é igual à
soma dos que estão em cima.
Qual será a próxima linha do triângulo?

4. Linha 0
C 00
1 Linha 1
1
C10 C11
1
C 02
1 C12
2 C 22
1
3
C0
1 C313 C2
3
3
C 33
1
C104 C4
4
1 C4
6
2 C4
4
3
C 44
1
Cada um dos elementos do triângulo de Pascal pode-se escrever na
forma de combinação.

5. Regularidades do Triângulo De Pascal
A Importância do 2º ELEMENTO DE UMA LINHA
1  Se o 2º elemento
é n a linha tem n+1
1 1
elementos.
1 2 1
1 3 3 1 O segundo elemento é 3, a linha tem
3+1 = 4 elementos.
1 4 6 4 1
O segundo elemento é 4, a linha tem
4+1 = 5 elementos.

6.  Se o 2º elemento é n a linha escreve – se:
1 C 00
1
1 1 C0 C11
1 2 1 C 02 C12 C 22
1 3 3 1
C 3
0
C13 3
C2 C 33
1 4 6 4 1
C 4
0 C
1
4
C 4
2 C 4
3
C 44
Generalizando
C 0n C1n C 2 C 3n C 4
n n ... C nn

7. Soma dos termos de cada linha: Soma:
1 1 = 20
1 + 1 2 = 21
1 + 2 + 1 4 = 2²
1+ 3 + 3 + 1 8 = 2³
1 +4 + 6 + 4 + 1 16 = 24
1 + 5 + 10 + 10 + 5 + 1 32 = 25
Se o 2º elemento é n a soma dos elementos da linha é:
2n

8. EXERCÍCIO:
De uma certa linha do Triângulo de Pascal, sabe-se que a
soma dos dois primeiros termos é 21.
Qual é o maior termo dessa linha?
Resposta:
184756

9. Propriedades Das Combinações
Propriedade 1
C 00
O primeiro e o último elementos de cada linhasão iguais a 1 1
C 0 C11
C0n 1 n
Cn 1 C 02 C12 C 22
C 03 C13 C 2 C33
3
Propriedade 2: Combinações complementares C 04 C14 C 24 C34 C 4
4
Observe a seguinte linha do triângulo
1 7 21 35 35 21 7 1 Generalizando
7 7
C3 C4
n n
C 7
2 C 7
5
C p C n p
7 7
C 1 C 6
7 7
C0 C7

10. Propriedade 3
Considere as seguintes linhas do triângulo:
Linha 6: 1 6 15 20 15 6 1
Linha 7: 1 7 21 35 35 21 7 1
6 + 15 = 21 20 + 15 = 35
C16 C2
6 7
C2 C 6
3 C 6
4 C 7
4
Generalizando Exemplos
8 8 9
C 4 C 5 C 5
n n n 1
C p C p 1 C p 1 18 18
C10 C11 19
C11

11. Propriedade 4
Soma dos termos de cada linha: Soma:
1 1 = 20
1 + 1 2 = 21
1 + 2 + 1 4 = 2²
1+ 3 + 3 + 1 8 = 2³
1 +4 + 6 + 4 + 1 16 = 24
1 + 5 + 10 + 10 + 5 + 1 32 = 25
• Considerando que cada linha do triângulo é formada pelas combinações de um
número natural, podemos concluir:
n n n n n n n
C 0 C 1 C 2 C 3 C 4 ... C n 2

12. Propriedade 5
Considere as seguintes linhas do triângulo:
Linha 6: 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64
Linha 7: 1 + 7 + 21 + 35 + 35 + 21 +7 +1 = 128
A soma da linha 6 é igual ao dobro da soma da linha 7 (6+1). 2 x 64
Generalizando
A soma de todas as combinações de n+1
elementos é o dobro de todas as
combinações de n elementos.
X2

13. Propriedades Das Combinações
C0n 1
n n
C p C n p
n n n 1
Cp Cp 1 Cp 1
C0 C1n C2 C3n C4 ... Cn
n n n n
2n
X2

14. A Professora: Rita
Fogageiro