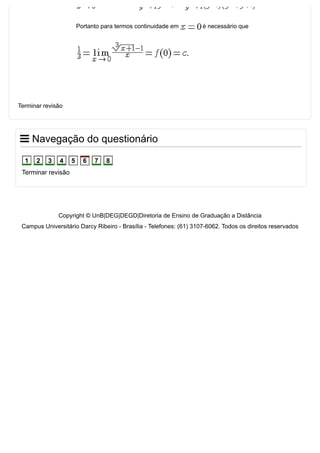
Este documento apresenta um teste online sobre continuidade de funções com 8 questões. O teste avalia o conhecimento do aluno sobre os limites laterais e a definição formal de continuidade para determinar valores que tornam funções contínuas em pontos específicos.

1. Página inicial / Meus cursos / Campus Planaltina / Licenciatura em Ciências Naturais / Cálculo
1 / 31 março ­ 6 abril / Teste Online 02
Questão 1
Correto
Atingiu 1,00 de
1,00
Marcar
questão
Questão 2
Iniciado em segunda, 30 Mar 2015, 23:02
Estado Finalizada
Concluída em segunda, 30 Mar 2015, 23:02
Tempo
empregado
26 segundos
Notas 6,50/8,00
Avaliar 8,13 de um máximo de 10,00(81%)
Para qual valor de a função
é contínua no ponto ?
Escolha uma:
nenhum.
.
.
qualquer
.
Note que
Logo, . Como existe o limite, para que seja contínua em
basta que .

2. Questão 2
Correto
Atingiu 1,00 de
1,00
Marcar
questão
Questão 3
Correto
Atingiu 1,00 de
1,00
Marcar
questão
Para qual valor de a função
é contínua em ?
Escolha uma:
nenhum.
.
qualquer
.
.
Dividindo o numerador pelo denominador obtemos
e portanto . Como
, para que seja contínua em devemos ter .
Para qual valor de a função
é contínua em ?
Escolha uma:
.
.
.
.
.

3. Questão 4
Correto
Atingiu 1,00 de
1,00
Marcar
questão
Questão 5
Parcialmente
correto
Atingiu 0,50 de
1,00
Temos que , e . Portanto,
para ser contínua em , precisamos ter que
.
Para qual valor de a função
é contínua em ?
Escolha uma:
Note que
Usando a expressão acima obtemos
Pela definição de continuidade em temos
Em um país imaginário o imposto de renda é cobrado da seguinte maneira:
aqueles que ganham até dez mil reais são isentos; os que ganham mais de dez
mil e até vinte mil reais pagam sobre a renda, menos um valor fixo
; de todos os demais é cobrada uma taxa de da renda. Sendo a
função que associa a cada renda o valor do imposto de renda a ser

4. 1,00
Marcar
questão
Questão 6
Incorreto
Atingiu 0,00 de
1,00
Marcar
questão
função que associa a cada renda o valor do imposto de renda a ser
pago, avalie as afirmações seguintes.
Escolha uma ou mais:
Se então é contínua em
é descontínua em
é uma função linear
Existe pelo menos um contribuinte que paga 3 mil reais de imposto
A função é dada por
A continuidade nos pontos e pode ser
analisado usando­se a definição de continuidade e o cálculo dos limites laterais.
Note que o ninguém paga 3 mil reais de imposto. De fato, qualquer que seja
, um contribuinte que ganha até 20 mil reais nunca paga mais de dois mil
reais de imposto. Assim, se existisse um contribuinte que pagasse três mil reais
de imposto, a sua renda deveria satisfazer a equação ,
isto é, .
Ocorre que, para essa renda, o imposto correto é
.
Considerando, para , a função
é correto afirmar que
O valor de para que seja contínua em é 5

5. Questão 7
Correto
Atingiu 1,00 de
1,00
Marcar
questão
O valor de para que seja contínua em é 3
O valor de para que seja contínua em é 10
A função é contínua em pois
No ponto temos que e
e portanto é contínua em desde que , isto é .
Para o estudo no ponto note primeiro que, se , então não existe
, pois o denominador se aproxima de e o numerador se
aproxima de um número diferente de . Porém, se temos que vale
zero em uma vizinha pequena à direita do ponto e portanto
. Como e
, concluímos que é contínua no ponto se .
Sejam e duas funções tais que é contínua em , é
descontínua em e não é identicamente nula. Neste caso, é possível
que o produto seja contínuo em .
Escolha uma opção:
Verdadeiro
Falso
De fato. Considere as funções

6. Questão 8
Correto
Atingiu 1,00 de
1,00
Marcar
questão
e
Note que é contínua em , pois
Por outro lado
e
Portanto, não é contínua em , contudo é contínua para todo
Para qual valor de a função
é contínua em ?
Escolha uma:
Seja Neste caso, obtemos

7. Copyright © UnB|DEG|DEGD|Diretoria de Ensino de Graduação a Distância
Campus Universitário Darcy Ribeiro ­ Brasília ­ Telefones: (61) 3107­6062. Todos os direitos reservados
Portanto para termos continuidade em é necessário que
Terminar revisão
 Navegação do questionário
Terminar revisão
1 2 3 4 5 6 7 8