O algoritmo de Floyd-Warshall se propõe a resolver o problema de encontrar o menor caminho entre todos os pares de vértices de um grafo orientado e ponderado. Ele utiliza programação dinâmica para calcular de forma eficiente as distâncias mínimas entre todos os pares de vértices do grafo.

1. Projeto e Análise de Algoritmo
Caminhos Mínimos: Floyd-Warshall
Universidade Federal do Amazonas (ICOMP)
Prof. Dr. Edleno Silva de Moura
Felipe André Souza da Silva1
, Jean Carlos A. de Figueiredo2
1
20 de Junho de 2017

2. Sumário
1. Introdução
2. O problema
3. Algoritmo
4. Aplicações
5. Exercícios
6. Referências
2

3. Introdução
3
● Também conhecido como algoritmo de Floyd, algoritmo de
Roy-Floyd, algoritmo de Roy-Warshall ou algoritmo WFI;
○ Foi explicado por Bernard Roy em 1959 e publicado 3 anos
mais tarde por Stephen Warshall e Robert Floyd.
● É um algoritmo que resolve o problema de encontrar o menor
caminho entre todos os pares de vértices de um grafo orientado
e ponderado;
○ Ele apenas encontra os valores de tais caminhos, e não a
seqüência de arestas a ser percorrida.

4. Introdução: Robert W. Floyd
4
● 08/06/1936; ♱ 25/09/2001 - (65 anos);
● Prof. emérito de Stanford;
● Ex-presidente do Dep. de Ciência da Computação;
● Algoritmo publicado 1962 baseado em programação dinâmica;
● Suas pesquisas incluem:
○ O projeto e análise dos algoritmos para encontrar trajetos curtos em uma rede;
○ Analisar linguagens de programação; selecionar e combinar permutações
aleatórias.
● Realização científica foi os métodos sistemáticos de verificação do programa.
“Assigning Meanings to Programs”.

5. Introdução: Robert W. Floyd
5
● Prêmio Turing em 1978
○ Metodologias na criação de software eficiente e confiável;
○ Teoria da análise;
○ Semântica das linguagens de programação;
○ Programa automático de verificação e síntese automática de programas;
○ Análise de algoritmos.

6. Introdução: Stephen Warshall
6
● 15/11/1935; ♱ 11/12/2006 - (71 anos);
● Bacharel em matemática em Harvard;
● Trabalhou no ORO (Operation Research Office) programa para fazer
pesquisas e desenvolvimento para o exército EUA;
● Algoritmo publicado 1962 baseado em programação dinâmica para encontrar
fechos transitivos em grafos;
● Contribuiu para o desenvolvimento da Ciência da Computação e Engenharia
de Software. Entre 1971 - 72, lecionou Eng. Soft. em universidades
francesas;
● Suas pesquisas incluem:
○ Desenvolvimento de S.O., design de compiladores, linguagens e
pesquisas operacionais.

7. 7
Introdução

8. Introdução
“Minha mensagem para programadores sérios é
esta: Passe parte do seu dia de trabalho examinando
e refinando seus próprios métodos, pois ainda que
estejam lutando para cumprir prazos, abstração
metodológica é um sábio investimento a longo
prazo.”
8
Robert W. Floyd

9. Problema: Menor caminho entre todos pares de vértices
9
Seja um grafo direcionado G = (V, E) com uma função de peso w: E →
R, onde R é o conjunto dos números reais, determine o menor
caminho (i.e., distância), entre todos os pares de vértices em G.
Assumindo que não há ciclos com custo zero ou negativo.
Ciclo negativoCiclo não negativo

10. Soluções anteriores abordadas em sala de aula
● Sol.1. Menor caminho de fonte única:
○ Se executar o algoritmo de Dijkstra;
● Sol.2. Menor caminho de destino único:
○ Inverter a direção das arestas e aplicar novamente Dijkstra;
● Sol.3. Menor Caminho entre quaisquer vértices u e v:
○ algoritmo de Dijkstra;
● Sol.4. Menor Caminho em grafos com pesos negativos:
○ algoritmo de Bellman-Ford;
Problema: Menor caminho entre todos pares de vértices
10

11. Soluções anteriores abordadas em sala de aula
● Sol.5. Menor caminho entre todos os pares de vértices :
○ Algoritmo de Floyd-Warshal;
Análise das opções:
● Se pesos não são negativos: Executar Dijkstra n vezes (para
cada vértice);
● Quanto custaria?
○ n × O((n + m)log n) = n × O(m log n) = O(nm log n) sendo O(n3
log n) para um grafo denso;
Problema: Menor caminho entre todos pares de vértices
11

12. Análise das opções:
● Se pesos fossem negativos:
○ executar algoritmo de Bellman-Ford n vezes (uma para cada
vértice);
● Quanto custaria?
○ n × O(nm)= O(n2
m) sendo O(n4
) para um grafo denso;
Problema: Menor caminho entre todos pares de vértices
12

13. Algoritmo de Floyd-Warshal
● Pode conter pesos negativos, mas não ciclos negativos;
● Grafo orientado G onde V(G) = {1, 2, 3, ..., n}, um subconjunto,
onde temos {1, 2, 3, ..., k};
● Algoritmo de programação dinâmica;
i. Caracterizar a estrutura de uma solução ótima;
ii. Definir recursivamente o valor de uma solução ótima;
iii. Computar o valor de uma solução ótima numa abordagem bottom-up.
Problema: Menor caminho entre todos pares de vértices
13

14. Algoritmo: Formato de Entrada e Saída
O algoritmo recebe como entrada uma matriz de adjacência que
representa um grafo G = (V, E) orientado e valorado.
Entrada: (wij
)
0 se i = j;
w(i,j) se i ≠ j e (i,j) ∈ E.
∞ se i ≠ j e (i,j) ∉ E.
(wij
) =
14
Uma Matriz Wnxn
representando os pesos das arestas do grafo de n
vértices, W = (wij
).
Saída: W

15. Algoritmo: Formato da entrada
15
Calculando as entrada dos pesos nos vértices i → j de G = (V, E).
a b
c d
2
6 7
1
3
∞
a b c d
0 ∞ 3 ∞
2 0 ∞
∞ 7 0 1
6 ∞ ∞ 0
a
b
c
d
j
i
k
W =

16. Algoritmo: Passo (i) na decomposição
Definição: Os vértices {v1
, v2
, ... vl-1
}, são chamados vértices
intermediários do caminho p = {v1
, v2
, ... vl
}.
16
i
j
todos os vértices intermediários {1, 2, .., k}
k
vértices em {1, 2, .., k-1}

17. Algoritmo: Passo (ii) na decomposição
Definir a matriz D(k)
, recursivamente, por meio de dij
(k)
, que irá
armazenar as distâncias calculadas do valor ótimo da solução para
todos os vértices i → j, tal que, os vértices intermediários estejam no
conjunto {1, 2, ..., k}.
● Dado um problema de caminho mínimo, não poderá existir um caminho
mais curto com o mesmo vértice mais de uma vez.
D(k)
= dij
(k)
17

18. Algoritmo: Passo (ii) na decomposição
● Considerando um menor caminho c do vértice i → j, onde todos os vértices
intermediários estão em {1, 2, ..., k}.
○ Se k ~ ∉ no vértice intermediário c, então di,j
(k)
= di,j
(k-1)
.
○ senão, k é um vértice intermediário: di,j
(k)
= min (di,j
(k-1)
, di,k
(k-1)
+ dk,j
(k-1)
)
● Com as observações anteriores, definimos dij
(k)
:
○
D(k)
= dij
(k)
18
wij
se k = 0;
min(di,j
(k-1)
, di,k
(k-1)
+ dk,j
(k-1)
) se k ≥ 1;
dij
(k)
=

19. Algoritmo: Passo (ii)
19
i
j
todos os vértices intermediários {1, 2, .., k}
k
vértices em {1, 2, .., k-1}
di,k
(k-1)
dk,j
(k-1)
di,j
(k-1)
di,j
(k-1)
= min(di,j
(k-1)
, di,k
(k-1)
+ dk,j
(k-1)
)

20. Algoritmo: Formato da saída
20
Calculando as entrada dos pesos nos vértices i → j de G = (V, E).
a b
c d
2
6 7
1
3
5
a b c d
0 10 3 4
2 0 6
7 7 0 1
6 16 9 0
a
b
c
d
j
i
k
D(k)
=

21. Algoritmo: Passo (iii)
21
O predecessor dos vértices i → j, do menor caminho, com todos vértices
intermediários no conjunto {1, 2, ..., k}. Onde:
∏(k)
= ( ij
(k)
)
ij
(k-1)
se di,i
(k-1)
≤ di,k
(k-1)
+ dk,j
(k-1)
kj
(k-1)
se di,i
(k-1)
> di,k
(k-1)
+ dk,j
(k-1)
ij
(k)
=
NULL se i = j ou wij
= ∞
i se i ≠ j e wij
< ∞ij
(k)
=
E

22. Algoritmo
22
Floyd-Warshall(W, n):
D(0)
= W
inicialização (∏(0)
)
para k = 1 até n:
para i = 1 até n:
para j = 1 até n:
se (di,j
(k-1)
≤ di,k
(k-1)
+ dk,j
(k-1)
):
di,j
(k)
= di,j
(k-1)
; ij
(k)
= ij
(k-1)
senão
di,j
(k)
= di,k
(k-1)
+ dk,j
(k-1)
;
ij
(k)
= kj
(k-1)
retorne D(n)
Análise
● Runtime: ϴ(n3
).
● A matriz predecessora pode ser
usada para extrair o menor
caminho;
● O algoritmo possui complexidade
de espaço ϴ(n3
), porém, é possível
reduzir essa complexidade para ϴ
(n2
) apenas utilizando uma matriz
ao invés de n.

23. Aplicações
O algoritmo, ainda pode ser utilizado em aplicações como:
● Calcular o Fecho Transitivo de um grafo;
● Verifica se um grafo não-dirigido é bipartido;
● Detectar ciclos negativos no grafo;
● Técnica de Rotulagem Floyd-Warshall;
● Acha um vértice central, i.e., o que minimiza a distância máxima ou
média entre todos os vértices;
23

24. Aplicações
● Poderíamos pensar, em como avaliar o melhor local para
instalarmos uma loja. Podemos definir como melhor local
aquele que diminui a distância entre a loja e locais estratégicos
como:
○ Um bairro onde o consumo dos produtos vendidos por ela é alto;
○ Estabelecimentos que presta serviços para a loja;
○ Local onde se tenha uma grande concentração de um público alvo
para a loja.
24

25. 1. O algoritmo de floyd-warshall se propõe a resolver que tipo de problema?
Exercícios
25

26. 1. O algoritmo de floyd-warshall se propõe a resolver que tipo de problema?
2. Quem foi o primeiro autor do algoritmo?
Exercícios
26

27. 1. O algoritmo de floyd-warshall se propõe a resolver que tipo de problema?
2. Quem foi o primeiro autor do algoritmo?
3. Qual é a técnica utilizada por este algoritmo? Ele pode ser considerado guloso?
justifique?
Exercícios
27

28. 1. O algoritmo de floyd-warshall se propõe a resolver que tipo de problema?
2. Quem foi o primeiro autor do algoritmo?
3. Qual é a técnica utilizada por este algoritmo? Ele pode ser considerado guloso?
justifique?
4. Dado um grafo:
a. Construa a matriz adjacente para o grafo;
b. Escreva a fórmula do cálculo recursivo de D(k)
em dij
(k)
Exercícios
28
3
2
2 1
3
8
5
2

29. 1. O algoritmo de floyd-warshall se propõe a resolver que tipo de problema?
a. Resolve o problema de encontrar o menor caminho entre todos os pares de vértices de um grafo
orientado e ponderado.
2. Quem foi o primeiro autor do algoritmo?
a. Bernard Roy
3. Qual é a técnica utilizada por este algoritmo? Ele pode ser considerado guloso? justifique?
a. Programação Dinâmica, não. P.D. é aplicável a problemas nos quais a solução ótima pode ser
computada a partir da solução ótima previamente calculada e memorizada.
4. Dado um grafo:
a. Construa a matriz adjacente para o grafo;
b. Mostre a fórmula do cálculo recursivo de dij
(k)
em D(k)
.
Exercícios
29
∞
1 2 3
0 8 5
3 0
∞ 2 0
1
2
3
W =
wij
se k = 0;
min(di,j
(k-1)
, di,k
(k-1)
+ dk,j
(k-1)
) se k ≥ 1;
dij
(k)
=

30. Perguntas
30

31. Ilustração Algoritmo Floyd’s
31
1
2
3
24
4
9
1 8
1
k = 0
1 2 3 4
0 8 ∞ 1
∞ 0 1 ∞
4 ∞ 0 ∞
∞ 2 9 0
1
2
3
4
j
i

32. Ilustração Algoritmo Floyd’s
32
k = 0
1 2 3 4
0 8 ∞ 1
∞ 0 1 ∞
4 ∞ 0 ∞
∞ 2 9 0
1
2
3
4
j
i
● Para o entendimento de todos, vou adotar aqui
uma técnica aqui não criada por mim, mas de
fácil compreensão. Vamos aos passos:
● Matriz de adjacência / custo: D0
[i,j]
1. Se i = j então MARQUE VERDE;

33. Ilustração Algoritmo Floyd’s
33
k = 0
1 2 3 4
0 8 ∞ 1
∞ 0 1 ∞
4 ∞ 0 ∞
∞ 2 9 0
1
2
3
4
j
i
● Para o entendimento de todos, vou adotar aqui
uma técnica aqui não criada por mim, mas de
fácil compreensão. Vamos aos passos:
● Matriz de adjacência / custo: D0
[i,j]
1. Se i = j então MARQUE VERDE;
2. Para cada i e j então MARQUE VERDE
CLARO;
3.

34. Ilustração Algoritmo Floyd’s
● Para o entendimento de todos, vou adotar aqui
uma técnica aqui não criada por mim, mas de
fácil compreensão. Vamos aos passos:
● Matriz de adjacência / custo: D0
[i,j]
1. Se i = j então MARQUE VERDE;
2. Para cada i e j então MARQUE VERDE
CLARO;
3. Para cada linha e coluna contendo
INFINITO, em i, j MARQUE VERDE
CLARO;
34
k = 0
1 2 3 4
0 8 ∞ 1
∞ 0 1 ∞
4 ∞ 0 ∞
∞ 2 9 0
1
2
3
4
j
i

35. Ilustração Algoritmo Floyd’s
35
k = 0
1 2 3 4
0 8 ∞ 1
∞ 0 1 ∞
4 ∞ 0 ∞
∞ 2 9 0
1
2
3
4
j
i
● Para o entendimento de todos, vou adotar aqui
uma técnica aqui não criada por mim, mas de
fácil compreensão. Vamos aos passos:
● Matriz de adjacência / custo: D0
[i,j]
1. Se i = j então MARQUE VERDE;
2. Para cada i e j então MARQUE VERDE
CLARO;
3. Para cada linha e coluna contendo
INFINITO, em i, j MARQUE VERDE
CLARO;
4. Se bloco == BRANCO então efetuar o
cálculo do menor caminho;
● CONGELA; CONGELA; CALCULA

36. Ilustração Algoritmo Floyd’s
36
k = 1
1 2 3 4
0 8 ∞ 1
∞ 0 1 ∞
4 12 0 5
∞ 2 9 0
1
2
3
4
j
i
● Matriz de distâncias D1
[i,j]:
○ D1
[3,2] = min {∞, c[3,1] + c[3,4]}
○ D1
[3,2] = min {∞, 4 + 8} = 12
■ ∞ < 12; sim; atualiza;
○ D1
[3,4] = min {∞, c[3,1] + c[1,4]}
○ D1
[3,4] = min {∞, 4 + 1} = 5
■ ∞ < 5; sim; atualiza;

37. Ilustração Algoritmo Floyd’s
37
k = 2
1 2 3 4
0 8 9 1
∞ 0 1 ∞
4 12 0 5
∞ 2 3 0
1
2
3
4
j
i
● Matriz de distâncias D2
[i,j]:
○ D2
[1,3] = min {∞, 8 (D1
[1,2]) + 1 (D1
[2,4])}
■ ∞ < 9; sim; atualiza;
○ D2
[4,3] = min {9, 2 (D1
[4,2]) + 1 (D1
[2,3])}
■ ∞ < 3; sim; atualiza;

38. Ilustração Algoritmo Floyd’s
38
k = 3
1 2 3 4
0 8 9 1
5 0 1 6
4 12 0 5
7 2 3 0
1
2
3
4
j
i
● Matriz de distâncias D3
[i,j]:
○ D3
[1,2] = min {8, 12 (D2
[3,2]) + 9 (D2
[1,3])}
■ 8 < 12 + 9; não; mantém;
○ D3
[1,4] = min {1, 2 (D2
[4,2]) + 1 (D2
[2,3])}
■ 1 < 9 + 5; não; mantém;
○ D3
[2,1] = min {∞, 4 (D2
[3,1]) + 1 (D2
[2,3])}
■ ∞ < 4 + 1; sim; atualiza;
○ D3
[2,4] = min {∞, 5 (D2
[3,4]) + 1 (D2
[2,3])}
■ ∞ < 5 + 1; sim; atualiza;
○ D3
[4,1] = min {∞, 4 (D2
[3,1]) + 3 (D2
[4,3])}
■ ∞ < 4 + 3; sim; atualiza;
○ D3
[4,2] = min {2, 12 (D2
[3,2]) + 3 (D2
[4,3])}
■ 2 < 12 + 3; não; mantém;

39. Ilustração Algoritmo Floyd’s
39
k = 4
1 2 3 4
0 3 4 1
5 0 1 6
4 7 0 5
7 2 3 0
1
2
3
4
j
i
● Matriz de distâncias D3
[i,j]:
○ D4
[1,2] = min {8, 2 (D3
[4,2]) + 1 (D3
[1,4])}
■ 8 < 2 + 1; sim; atualiza;
○ D4
[1,3] = min {9, 3 (D3
[4,3]) + 1 (D3
[1,4])}
■ 9 < 3 + 1; sim; atualiza;
○ D4
[2,1] = min {5, 7 (D3
[4,1]) + 6 (D3
[2,4])}
■ 5 < 7 + 6; não; mantém;
○ D4
[2,3] = min {1, 3 (D3
[4,3]) + 1 (D3
[1,4])}
■ 1 < 3 + 1; não; mantém;
○ D4
[3,1] = min {4, 7 (D3
[4,1]) + 5 (D3
[3,5])}
■ 4 < 7 + 5; não; mantém;
○ D4
[3,2] = min {12, 2 (D3
[4,2]) + 5 (D3
[3,5])}
■ 12 < 2 + 5; sim; atualiza;

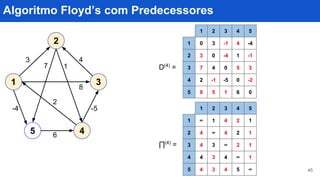
40. Algoritmo Floyd’s com Predecessores
40
algoritmo FloydPred(grafo ponderado (G,c)):
D ← c Crie matriz de distância inicial a partir de pesos.
∏ ← ∏(0)
Inicialize predecessores de c com ∞.
para k = 1 até n:
para i = 1 até n:
para j = 1 até n:
se ( D[i,j] > d[i,k] + d[k,j] ) então
D[i,j] ← D[i,k] + D[k,j] ; [i,j] ← [k,j]
retorne D(n)

41. Algoritmo Floyd’s com Predecessores
41
2
5
31
-5
4
4
17
3
2
6
-4
8
1 2 3 4
0 3 8 ∞
∞ 0 ∞ 1
∞ 4 0 ∞
2 ∞ -5 0
1
2
3
4
5
5 ∞ ∞ ∞ 6
-4
7
∞
∞
0
D(0)
=
1 2 3 4
∞ 1 1 ∞
∞ ∞ ∞ 2
∞ 3 ∞ ∞
4 ∞ 4 ∞
1
2
3
4
5
5 ∞ ∞ ∞ 5
1
2
∞
∞
∞
∏(0)
=

42. Algoritmo Floyd’s com Predecessores
42
2
5
31
-5
4
4
17
3
2
6
-4
8
1 2 3 4
0 3 8 ∞
∞ 0 ∞ 1
∞ 4 0 ∞
2 5 -5 0
1
2
3
4
5
5 ∞ ∞ ∞ 6
-4
7
∞
-2
0
D(1)
=
1 2 3 4
∞ 1 1 ∞
∞ ∞ ∞ 2
∞ 3 ∞ ∞
4 1 4 ∞
1
2
3
4
5
5 ∞ ∞ ∞ 5
1
2
∞
1
∞
∏(1)
=

43. Algoritmo Floyd’s com Predecessores
43
2
5
31
-5
4
4
17
3
2
6
-4
8
1 2 3 4
0 3 8 4
∞ 0 ∞ 1
∞ 4 0 5
2 5 -5 0
1
2
3
4
5
5 ∞ ∞ ∞ 6
-4
7
11
-2
0
D(2)
=
1 2 3 4
∞ 1 1 2
∞ ∞ ∞ 2
∞ 3 ∞ 2
4 1 4 ∞
1
2
3
4
5
5 ∞ ∞ ∞ 5
1
2
2
1
∞
∏(2)
=

44. Algoritmo Floyd’s com Predecessores
44
2
5
31
-5
4
4
17
3
2
6
-4
8
1 2 3 4
0 3 8 4
∞ 0 ∞ 1
∞ 4 0 5
2 -1 -5 0
1
2
3
4
5
5 ∞ ∞ ∞ 6
-4
7
11
-2
0
D(3)
=
1 2 3 4
∞ 1 1 2
∞ ∞ ∞ 2
∞ 3 ∞ 2
4 3 4 ∞
1
2
3
4
5
5 ∞ ∞ ∞ 5
1
2
2
1
∞
∏(3)
=

45. Algoritmo Floyd’s com Predecessores
45
2
5
31
-5
4
4
17
3
2
6
-4
8
1 2 3 4
0 3 -1 4
3 0 -4 1
7 4 0 5
2 -1 -5 0
1
2
3
4
5
5 8 5 1 6
-4
-1
3
-2
0
D(4)
=
1 2 3 4
∞ 1 4 2
4 ∞ 4 2
4 3 ∞ 2
4 3 4 ∞
1
2
3
4
5
5 4 3 4 5
1
1
1
1
∞
∏(4)
=

46. Algoritmo Floyd’s com Predecessores
46
2
5
31
-5
4
4
17
3
2
6
-4
8
1 2 3 4
0 1 -3 2
3 0 -4 1
7 4 0 5
2 -1 -5 0
1
2
3
4
5
5 8 5 1 6
-4
-1
3
-2
0
D(5)
=
1 2 3 4
∞ 3 4 5
4 ∞ 4 2
4 3 ∞ 2
4 3 4 ∞
1
2
3
4
5
5 4 3 4 5
1
1
1
1
∞
∏(5)
=

47. Referências
● CORMEN, T. H.; LEISERSON, C. E.; RIVEST, R. L. e STEIN, C. Introduction to Algorithms, 3a
ed, MIT
Press, 2009.
● Floyd, R. W. (1962). Algorithm 97: shortest path.Communications of the ACM, 5(6):345.
● Roy, Bernard (1959). "Transitivité et connexité.". C. R. Acad. Sci. Paris. 249: 216–218.
● Warshall, Stephen (January 1962). "A theorem on Boolean matrices". Journal of the ACM. 9 (1): 11–12.
● MONTEFORTE, Arthur. Algoritmo de Floyd-Warshall. Disponível em:
<https://www.youtube.com/watch?v=cEmvog65dX0>. Acesso em: 20 de maio de 2017.
● Knuth, Donald E. "Memorial Resolution: Robert W. Floyd (1936-2001)" (PDF). Stanford University Faculty
Memorials. Stanford Historical Society.
● FLOYD, Robert W. Professor Robert W. Floyd. Disponível em:
<https://www-cs.stanford.edu/memoriam/professor-robert-w-floyd>. Acesso em: 20 de maio de 2017.
● Shin, H. and Shin, J. S. (2006). Application of floyd-warshall labelling technique: Identification of
connected pixel components in binary image. Korean Journal of Mathematics, 14(1):47–55.
47