Otimizador de Rotas - PythonBrasil[6]

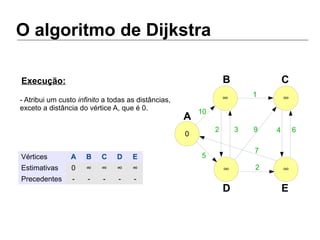
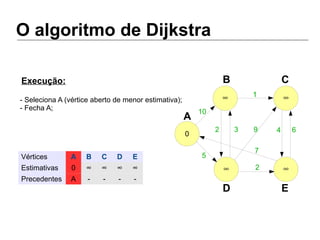
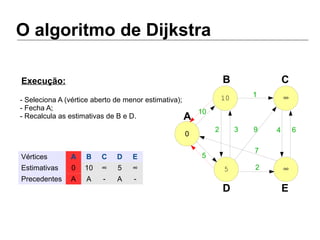
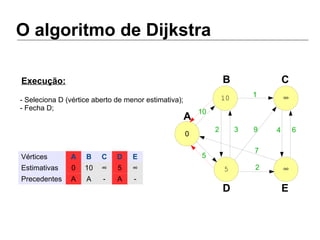
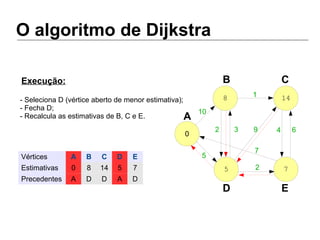
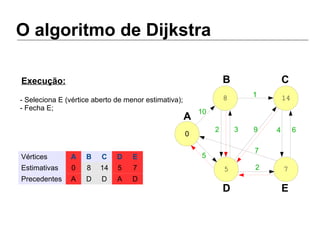
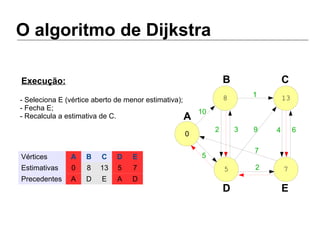
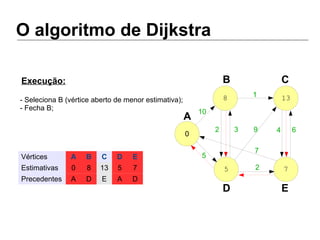
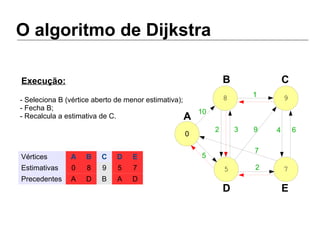
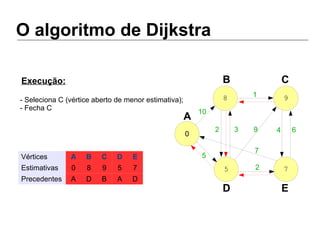
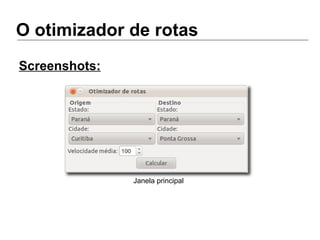
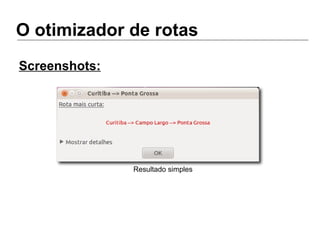
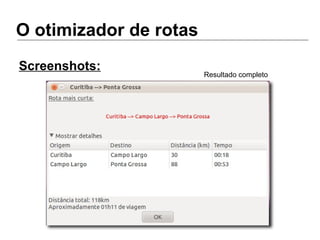
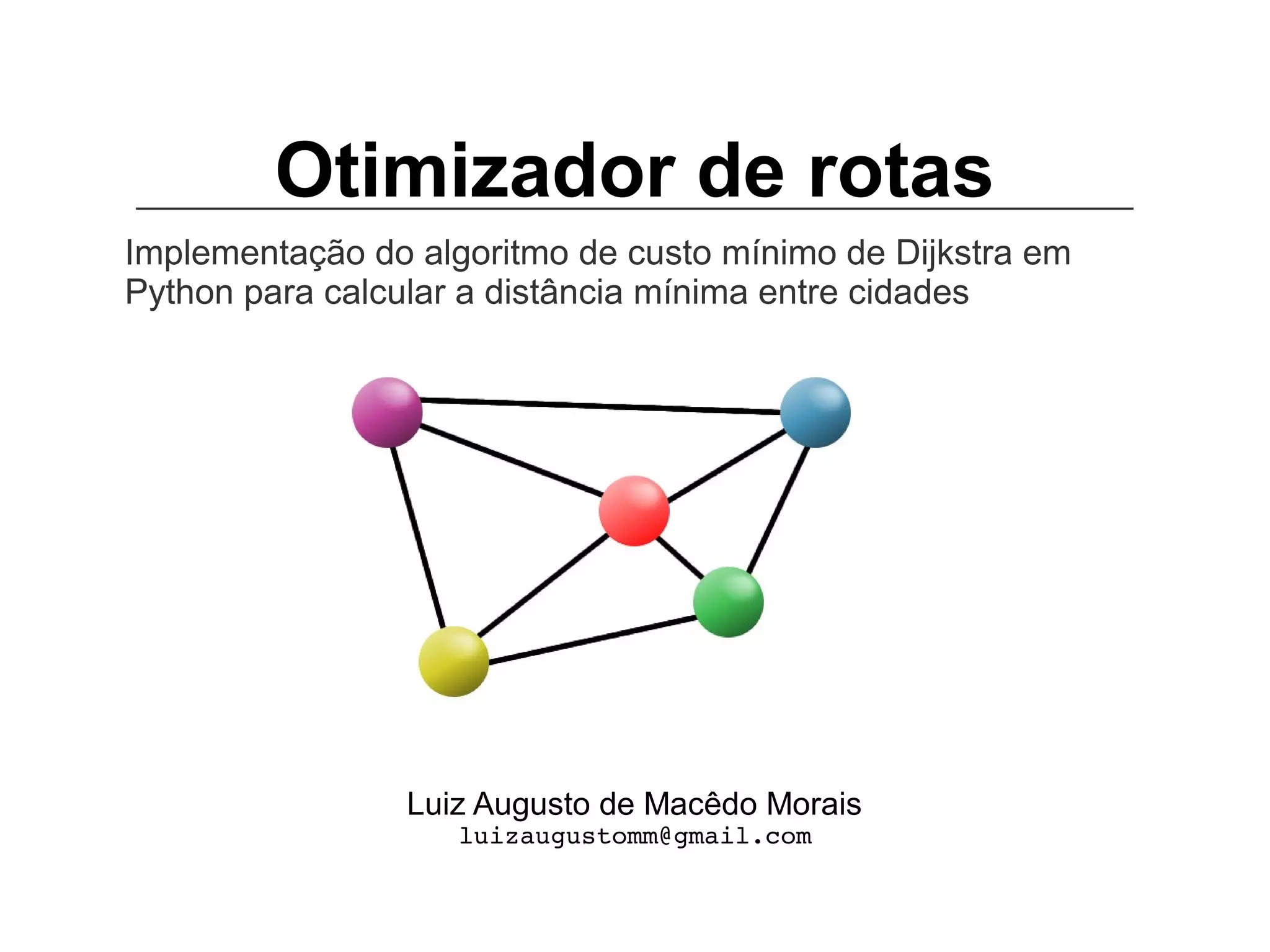
Otimizador de rotas
Implementação do algoritmo de custo mínimo de Dijkstra em
Python para calcular a distância mínima entre cidades
Luiz Augusto de Macêdo Morais
luizaugustomm@gmail.com

Quem sou eu
✔ 18 anos;
✔ Graduando em Licenciatura em Computação – UEPB;
✔ Monitor da disciplina de Linguagem de Programação I
– Python;
✔ Faz parte do grupo de pesquisa “Genética e Evolução
de Plantas do Semiárido” e utiliza o Python na
pesquisa;
✔ Conheceu a linguagem Python há um ano.

Roteiro
● Objetivos
● Quem foi Dijkstra?
● O algoritmo de Dijkstra
● Afinal, pra que serve este algoritmo?
● Implementação do algoritmo em Python
● O otimizador de rotas
● Dúvidas

Objetivos
✔ Mostrar quem foi Dijkstra
✔ Explicar o funcionamento do algoritmo de Dijkstra
✔ Exibir um exemplo prático do algoritmo, utilizando a
linguagem Python
✔ Explicar qual é a proposta do programa Otimizador de
rotas
✔ Expor as futuras funcionalidades do software

Quem foi Dijkstra?
Edsger Wybe Dijkstra
(1930 - 2002)
● Matemático e cientista da computação
● Áreas de atuação:
● Algoritmos;
● Linguagens de programação;
● Sistemas operacionais, etc.
● Criou o primeiro compilador para a
linguagem ALGOL 60
● Foi contrário ao comando GOTO
● A Case against the GO TO Statement (1968)
● Criador do algoritmo do caminho mais
curto (shortest path)

Quem foi Dijkstra?
Edsger Wybe Dijkstra
(1930 - 2002)
Prêmios e titulações:
● Membro da Sociedade Britânica de
Computação (1971)
● Prêmio Turing (1972)
● Prêmio AFIPS Harry Goode (1974)
● Prêmio de pioneiro da computação do
IEEE (1982)
● Prêmio ACM SIGCSE para
contribuições proeminentes à
instrução da ciência da computação
(1989)

O algoritmo de Dijkstra
● Encontra o menor caminho entre dois
vértices de um grafo
● Não funciona com arestas de peso
negativo. Para isso, usa-se o algoritmo de
Bellman-Ford
● Complexidade O(|V|²)
● O(|E| + |V| * log|V|) (heap de Fibonacci)
Características:

# Inicia-se os valores
para todo v V[G]∈
dist[v]← ∞
prec[v] ← nulo
dist[s] ← 0
Q ← V[G] # Conjunto dos vértices abertos
S ← ø # Conjunto dos vértices fechados
# Relaxamento das arestas
enquanto Q ≠ ø
u ← extraia-mín(Q)
S ← S {u}∪
para cada v adjacente a u
se dist[v] > dist[u] + w(u, v)
então dist[v] ← dist[u] + w(u, v)
prec[v] ← u
Pseudocódigo:

∞ ∞
∞ ∞
0
A
B C
D E
10
5
2 3
1
9
7
2
4 6
Vértices A B C D E
Estimativas 0 ∞ ∞ ∞ ∞
Precedentes - - - - -
- Atribui um custo infinito a todas as distâncias,
exceto a distância do vértice A, que é 0.
Execução:

∞ ∞
∞ ∞
0
A
B C
D E
10
5
2 3
1
9
7
2
4 6
Vértices A B C D E
Estimativas 0 ∞ ∞ ∞ ∞
Precedentes A - - - -
- Seleciona A (vértice aberto de menor estimativa);
- Fecha A;
Execução:

5 ∞
10 ∞
0
A
B C
D E
Vértices A B C D E
Estimativas 0 10 ∞ 5 ∞
Precedentes A A - A -
10
5
2 3
1
9
7
2
4 6
- Seleciona A (vértice aberto de menor estimativa);
- Fecha A;
- Recalcula as estimativas de B e D.
Execução:

5 ∞
10 ∞
0
A
B C
D E
Vértices A B C D E
Estimativas 0 10 ∞ 5 ∞
Precedentes A A - A -
10
5
2 3
1
9
7
2
4 6
- Seleciona D (vértice aberto de menor estimativa);
- Fecha D;
Execução:

5 7
8 14
0
A
B C
D E
Vértices A B C D E
Estimativas 0 8 14 5 7
Precedentes A D D A D
10
5
2 3
1
9
7
2
4 6
- Seleciona D (vértice aberto de menor estimativa);
- Fecha D;
- Recalcula as estimativas de B, C e E.
Execução:

5 7
8 14
0
A
B C
D E
Vértices A B C D E
Precedentes A D D A D
10
5
2 3
1
9
7
2
4 6
- Seleciona E (vértice aberto de menor estimativa);
- Fecha E;
Execução:

5 7
8 13
0
A
B C
D E
Vértices A B C D E
Precedentes A D E A D
10
5
2 3
1
9
7
2
4 6
- Seleciona E (vértice aberto de menor estimativa);
- Fecha E;
- Recalcula a estimativa de C.
Execução:

5 7
8 13
0
A
B C
D E
Vértices A B C D E
Precedentes A D E A D
10
5
2 3
1
9
7
2
4 6
- Seleciona B (vértice aberto de menor estimativa);
- Fecha B;
Execução:

5 7
8 9
0
A
B C
D E
Vértices A B C D E
Precedentes A D B A D
10
5
2 3
1
9
7
2
4 6
- Seleciona B (vértice aberto de menor estimativa);
- Fecha B;
- Recalcula a estimativa de C.
Execução:

5 7
8 9
0
A
B C
D E
Vértices A B C D E
Precedentes A D B A D
10
5
2 3
1
9
7
2
4 6
- Seleciona C (vértice aberto de menor estimativa);
- Fecha C
Execução:

Afinal, pra que serve este algoritmo?
● Linhas de transmissão elétrica
● Conexão de redes
● Panejamento de movimentos de um robô
● Planejamento de rotas e tempo de viagens

Implementação do algoritmo em Python

O otimizador de rotas
● Auxilia em viagens de percursos
desconhecidos;
● Calcula a rota mínima entre cidades;
● Mostra passo a passo o percurso escolhido;
● Informa a distância e o tempo total de viagem;
● Não necessita de conexão com a Internet.
Características:

Screenshots:
Janela principal

Screenshots:
Resultado simples

Screenshots:
Resultado completo

● Exibir o mapa da rota escolhida;
● Informar a rota mais rápida;
● Aumentar o número de cidades e Estados;
● Exibir informações sobre pedágios e tipo de
estrada;
● Otimizar o algoritmo.
Próximos passos:

Obrigado!
Twitter: @luizaugustomm
E-mail: luizaugustomm@gmail.com
Site: http://ola-mundo.com

Referências
Edsger Dijkstra. Disponível em: <http://pt.wikipedia.org/wiki/Edsger_Dijkstra>.
Acesso em: 8 de outubro de 2010.
Algoritmo de Dijkstra. Disponível em:
<http://pt.wikipedia.org/wiki/Algoritmo_de_Dijkstra>. Acesso em: 8 de outubro de
2010.
Algoritmo de Dijkstra para cálculo do Caminho de Custo Mínimo. Disponível em:
<http://www.inf.ufsc.br/grafos/temas/custo-minimo/dijkstra.html>. Acesso em: 8 de
outubro de 2010.
LEMOS, G. Otimização de Rotas Rodoviárias Utilizando o Algoritmo de Dijkstra
e a API do Google Maps. 2009. 24f. Universidade Estadual de Londrina. Londrina,
Paraná, 2009.
MÉNDEZ, Y. S.; GUARDIA, L. E. T. Problema do caminho mais curto:
Algoritmo de Dijkstra. Universidade Federal Fluminense. Rio de Janeiro, Rio
de Janeiro, 2008.

Otimizador de Rotas - PythonBrasil[6]

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Otimizador de Rotas - PythonBrasil[6]

Mais de Luiz Augusto Macêdo Morais

Otimizador de Rotas - PythonBrasil[6]