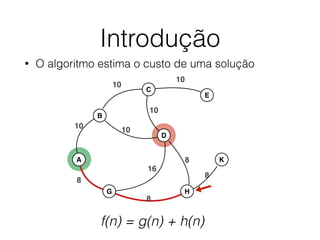
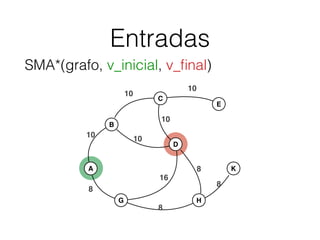
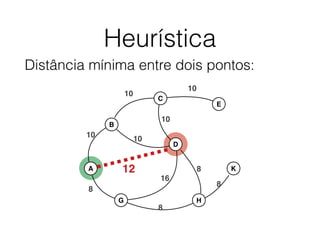
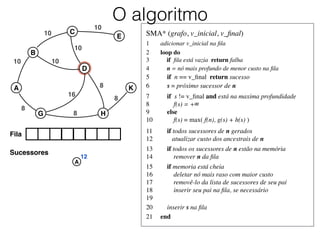
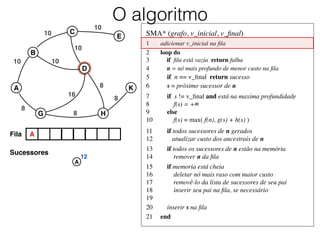
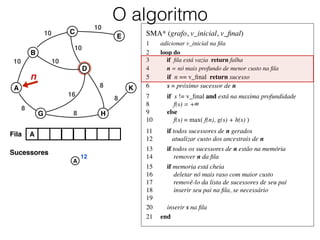
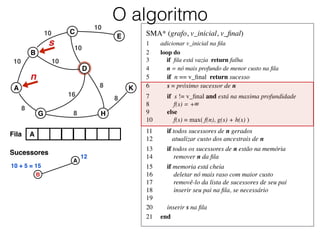
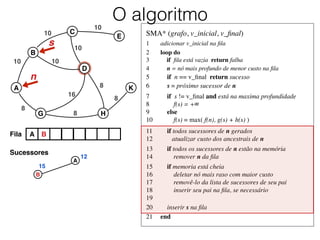
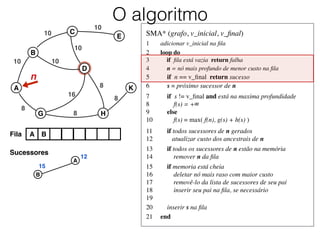
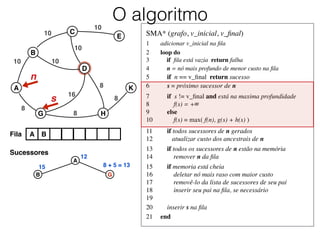
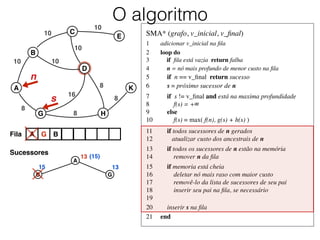
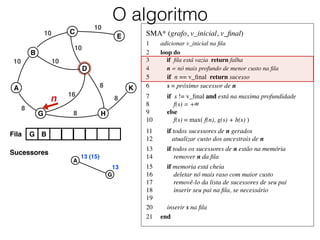
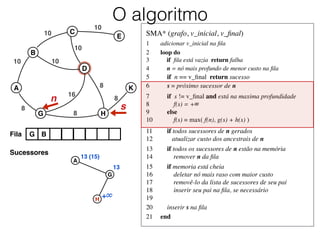
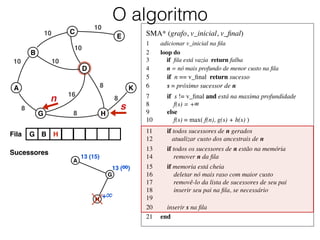
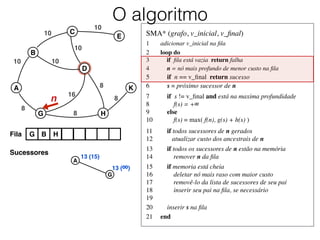
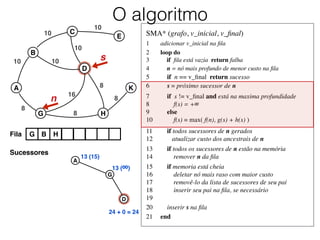
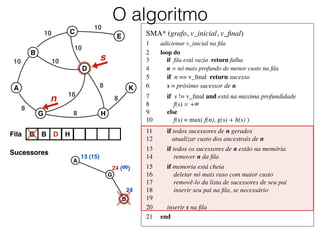
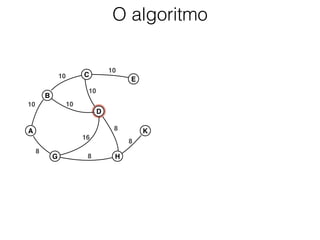
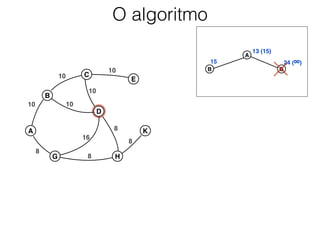
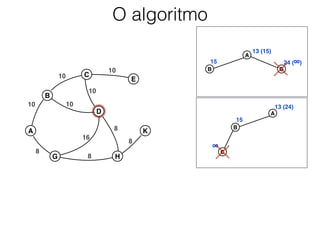
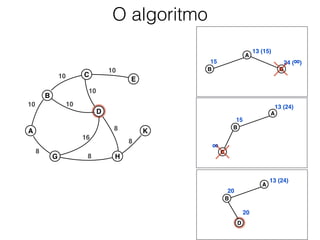
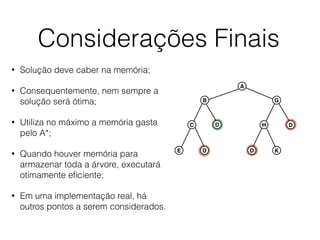
O documento descreve o algoritmo SMA* (Simplified Memory-Bounded A*), que é uma variação do algoritmo A* projetada para lidar com restrições de memória. O SMA* explora os nós da fronteira de maneira semelhante ao A*, mas pode esquecer nós antigos para liberar memória quando necessário, garantindo assim que sempre encontre a solução ótima se houver espaço suficiente na memória.

1. SMA*
Fernando Simeone
Mestrado em Ciência da Computação
Universidade Federal de Lavras
!
Projeto e Análise de Algoritmos (2014/2)

2. Tópicos
• Introdução
• O algoritmo
• Desempenho
• Considerações finais
• Referências

3. Introdução

4. Introdução

5. Introdução
• O problema de memória do algoritmo A*;

6. Introdução
• O problema de memória do algoritmo A*;
• SMA* (Simplified Memory-Bounded);

7. Introdução
• O problema de memória do algoritmo A*;
• SMA* (Simplified Memory-Bounded);
• Principais dificuldades:

8. Introdução
• O problema de memória do algoritmo A*;
• SMA* (Simplified Memory-Bounded);
• Principais dificuldades:
• Garantir a solução ótima;

9. Introdução
• O problema de memória do algoritmo A*;
• SMA* (Simplified Memory-Bounded);
• Principais dificuldades:
• Garantir a solução ótima;
• Evitar expansão repetida de nós esquecidos.

10. Introdução
• O algoritmo estima o custo de uma solução
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
f(n) = g(n) + h(n)

11. O algoritmo

12. Entradas
SMA*(grafo, v_inicial, v_final)
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8

13. Heurística
Distância mínima entre dois pontos:
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
12

14. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
12
A

15. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila A
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
12
A

16. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila A
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
12
A
n

17. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila A
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
12
n
A
B
10 + 5 = 15
s

18. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila A B
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
12
n
A
B
15
s

19. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila A B
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
12
n
A
B
15

20. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila A B
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
n
A
B G
12
15
s
8 + 5 = 13

21. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila A G B
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
n
A
B G
13
15
s
13
(15)

22. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila G B
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
A
G
13 (15)
n
13

23. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila G B
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
n
s
A
G
H
13 (15)
13
+∞

24. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila G B H
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
n
s
A
G
H
13 (15)
+∞
13 (∞)

25. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila G B H
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
n
A
G
13 (15)
13 (∞)

26. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila G B H
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
n
s
A
G
D
13 (15)
13 (∞)
24 + 0 = 24

27. SMA* (grafo, v_inicial, v_final)
1
adicionar v_inicial na fila
2
loop do
3
if fila está vazia return falha
4
n = nó mais profundo de menor custo na fila
5
if n == v_final return sucesso
6
s = próximo sucessor de n
7
if s != v_final and está na maxima profundidade
8
f(s) = +∞
9
else
10
f(s) = max( f(n), g(s) + h(s) )
11
if todos sucessores de n gerados
12
atualizar custo dos ancestrais de n
13
if todos os sucessores de n estão na memória
14
remover n da fila
15
if memoria está cheia
16
deletar nó mais raso com maior custo
17
removê-lo da lista de sucessores de seu pai
18
inserir seu pai na fila, se necessário
19
20
inserir s na fila
21
end
O algoritmo
Fila G B D H
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8
Sucessores
A
n
s
A
G
D
13 (15)
24 (∞)
24

28. O algoritmo
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8

29. O algoritmo
A
B G
13 (15)
15 24 (∞)
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8

30. O algoritmo
A
B G
13 (15)
15 24 (∞)
A
B
C
15
∞
13 (24)
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8

31. O algoritmo
A
B G
13 (15)
15 24 (∞)
A
B
C
15
∞
13 (24)
A
B
D
13 (24)
20
20
A
B
C
D
E
G H
K
10
10
10
10
10
8
8
16
8
8

32. Desempenho

33. Desempenho
Nós expandidos X memória

34. Desempenho
Nós expandidos X memória
Com +/- 32% da memória gasta pelo A* consegue efetuar o
mesmo número de expansões

35. Considerações Finais

36. Considerações Finais
A
B G
C D
E D
H D
D K

37. Considerações Finais
• Solução deve caber na memória;
A
B G
C D
E D
H D
D K

38. Considerações Finais
• Solução deve caber na memória;
• Consequentemente, nem sempre a
solução será ótima;
A
B G
C D
E D
H D
D K

39. Considerações Finais
• Solução deve caber na memória;
• Consequentemente, nem sempre a
solução será ótima;
• Utiliza no máximo a memória gasta
pelo A*;
A
B G
C D
E D
H D
D K

40. Considerações Finais
• Solução deve caber na memória;
• Consequentemente, nem sempre a
solução será ótima;
• Utiliza no máximo a memória gasta
pelo A*;
• Quando houver memória para
armazenar toda a árvore, executará
otimamente eficiente;
A
B G
C D
E D
H D
D K

41. Considerações Finais
• Solução deve caber na memória;
• Consequentemente, nem sempre a
solução será ótima;
• Utiliza no máximo a memória gasta
pelo A*;
• Quando houver memória para
armazenar toda a árvore, executará
otimamente eficiente;
• Em uma implementação real, há
outros pontos a serem considerados.
A
B G
C D
E D
H D
D K

42. Referências
Russell, S. (1992). Efficient memory-bounded search methods. In
Proceedings of the 10th European Conference on Artificial Intelligence,
ECAI ’92, pages 1–5, New York, NY, USA. John Wiley & Sons, Inc.!
!
Russell, S. J. and Norvig, P. (2003). Artificial intelligence: A modern
approach. pages 101–111. Pearson Education, 2 edition.!
!

43. Obrigado
Dúvidas?