Este documento resume a Transformada Rápida de Fourier (FFT). Em 3 frases: A FFT foi desenvolvida por Cooley e Tukey em 1965 para reduzir a complexidade computacional da Transformada de Fourier Discreta de O(N2) para O(NlogN). A FFT decompõe uma DFT em DFTs menores através de uma divisão recursiva da sequência de entrada. Isso permite calcular uma DFT de N pontos com menos operaçoes do que o algoritmo direto, tornando a FFT muito útil para análises espectrais e outros processamentos de sinal

1. Transformada R´pida de Fourier
a
L. S. Sousa, M. B. Rodrigues
Instituto Federal do Cear´
a
lucasssousa10@gmail.com, murillobarata1@gmail.com
December 9, 2013
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
1 / 48

2. ´
Indice
1
2
3
4
Conceitos B´sicos
a
S´ries de Fourier
e
Transformada de Fourier
Representa¸˜o de Sinais
ca
Ra´ Complexas da Unidade
ızes
Transformada Discreta de Fourier
Defini¸˜o
ca
Transformada R´pida de Fourier
a
Introdu¸˜o
ca
Algoritmo de Cooley-Tukey
Passo-a-Passo
An´lise da Complexidade Parcial
a
Continuando com a melhoria
An´lise da Complexidade
a
Borboleta
Algoritmo de Cooley-Tukey
Referˆncias e Agradecimentos
e
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
2 / 48

3. S´ries de Fourier
e
Figure: Jean Baptiste Joseph Fourier
S´ries de Fourier
e
“Qualquer fun¸˜o peri´dica, por mais complicada que seja, pode ser
ca
o
decomposta a partir de uma soma de senos e cossenos”
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
3 / 48

4. S´ries de Fourier
e
S´ries de Fourier
e
Uma s´rie de fourier decomp˜e fun¸˜es peri´dicas ou sinais peri´dicos para
e
o
co
o
o
a soma de um conjunto, possivelmente finito, de fun¸oes simples de
c˜
oscila¸˜o(Senos e Cossenos). (Wikipedia)
ca
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
4 / 48

5. S´ries de Fourier
e
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
5 / 48

6. Transformada de Fourier
A Transformada de Fourier ´ deduzida atrav´s das S´ries de
e
e
e
Fourier.
´
E utilizada para mudar o dom´
ınio de uma Representa¸˜o de Sinal.
ca
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
6 / 48

7. Representa¸˜o de Sinais
ca
Um sinal, naturalmente, ´ representado no dom´
e
ınio do tempo.
Exibe um grupo de caracter´
ısticas do sinal.
Figure: Sinal no dom´ do tempo
ınio
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
7 / 48

8. Representa¸˜o de Sinais
ca
Para que algumas caracter´
ısticas do sinal sejam exibidas, ´ necess´rio
e
a
que ele esteja no Dom´
ınio da Frequˆncia.
e
Exibe outro grupo de caracter´
ısticas do sinal.
Figure: Sinal no dom´ da frequˆncia.
ınio
e
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
8 / 48

9. Ra´ Complexas da Unidade
ızes
Uma n-´sima raiz complexa da unidade ´ um n´mero W tal que:
e
e
u
Wn = 1
Existem exatamente n ra´ n-´simas complexas da unidade, que s˜o:
ızes e
a
e
2πik
n
, para k = 0, 1, ..., n-1
e iu = cos(u) + isen(u)
O valor Wn = e
2πi
n
´ a principal ra´ complexa da unidade, assim:
e
ız
0
1
2
n−1
Wn , Wn , Wn , ..., Wn . S˜o as n ra´ da unidade.
a
ızes
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
9 / 48

10. Ra´ Complexas da Unidade
ızes
Formam o grupo aditivo (Zn , +) m´dulo n.
o
n
0
Wn = Wn = 1
(j+k)mod(n)
j
j+k
k
Wn Wn = Wn = Wn
−1
n−1
Wn = Wn
Figure: Raizes Complexas n = 8
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
10 / 48

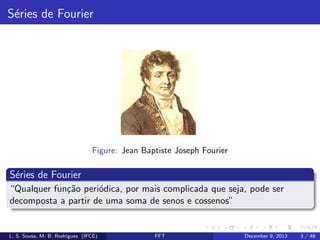
11. Transformada Discreta de Fourier
Considere a sequˆncia x[n] que ´ peri´dica em tempo T, ou seja.
e
e
o
x[n] = x[n + rT ], ∀r Z
(1)
Tal sequˆncia pode ser representada por uma s´rie de Fourier,
e
e
correspondendo ` soma de sequˆncias exponenciais relacionadas
a
e
harmonicamente.
∞
i2πmn
1
x[n] =
X [m]e N
N m
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
(2)
11 / 48

12. Transformada Discreta de Fourier
A representa¸˜o em s´rie de Fourier de um sinal peri´dico cont´
ca
e
o
ınuo
no tempo, geralmente, precisa de infinitas exponenciais complexas.
No entanto, a S´rie de Fourier para qualquer sinal discreto no tempo
e
com per´
ıodo N requer apenas N exponenciais complexas j´ que elas
a
s˜o peri´dicas.
a
o
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
12 / 48

13. Transformada Discreta de Fourier
Assim, a representa¸˜o torna-se:
ca
x[n] =
1
N
N−1
X [m]e
i2πmn
N
(3)
m=0
E os coeficientes da s´rie de Fourier X[m] s˜o obtidos a partir de x[n]
e
a
pela rela¸˜o.
ca
N−1
X [m] =
x[n]e
−i2πmn
N
(4)
n=0
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
13 / 48

14. Transformada Discreta de Fourier
2π
Se fizermos Wn = e −i( N ) Temos que:
Equa¸˜o de An´lise:
ca
a
N−1
kn
x[n]WN
X [k] =
n=0
(5)
(DFT )
Equa¸˜o de S´
ca
ıntese:
X [k] =
L. S. Sousa, M. B. Rodrigues (IFCE)
1
N
N−1
−kn
X [k]WN
k=0
(6)
(IDFT )
FFT
December 9, 2013
14 / 48

15. Transformada Discreta de Fourier
Alta complexidade computacional com custo assint´tico de O(n2 )
o
Para diminuir essa complexidade, ´ proposto o uso da Transformada
e
R´pida de Fourier.
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
15 / 48

16. Introdu¸˜o
ca
Algoritmo criado em 1965
Autores: J.W. Cooley(IBM) e J.W. Tukey(Bell Labs)
Dividir a subsequˆncia x[n] em duas sequˆncias.
e
e
Decima¸˜o em Tempo
ca
Algoritmos no qual a sequˆncia ´ decomposta sucessivamente em
e
e
sequˆncias menores.
e
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
16 / 48

17. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
17 / 48

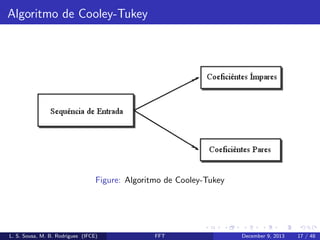
18. Algoritmo de Cooley-Tukey
∞
∞
nk
x[n]WN
X (k) =
nPar
nk
x[n]WN
+
(7)
nImpar
Fazendo n = 2r e n = 2r + 1, temos que:
N/2−1
N/2−1
2rk
x[2r ]WN
X (k) =
(2r +1)k
+
r =0
x[2r + 1]WN
N/2−1
N/2−1
2 rk
x[2r ](WN )
X (k) =
+
r =0
L. S. Sousa, M. B. Rodrigues (IFCE)
(8)
r =0
k
WN
2
x[2r + 1](WN )
rk
(9)
r =0
FFT
December 9, 2013
18 / 48

19. Algoritmo de Cooley-Tukey
2
Mas WN = WN/2 j´ que:
a
2π
2
WN = e −2i( N ) = e
π
−2i( (N/2) )
= WN/2
Logo (9) pode ser reescrito como:
N/2−1
N/2−1
rk
x[2r ]WN/2
X (k) =
+
r =0
k
WN
rk
x[2r + 1]WN/2
k
X (k) = G [k] + WN H[k]
L. S. Sousa, M. B. Rodrigues (IFCE)
(10)
r =0
FFT
(11)
December 9, 2013
19 / 48

20. Algoritmo de Cooley-Tukey
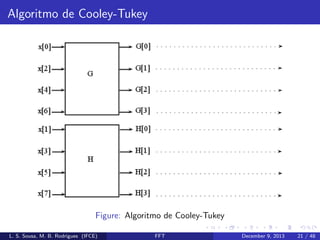
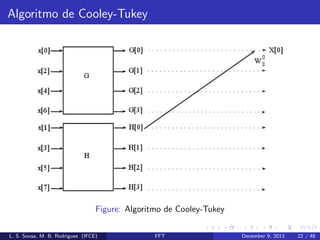
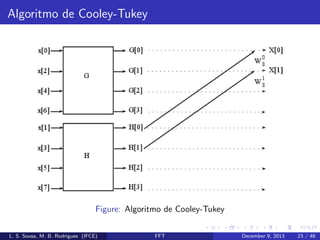
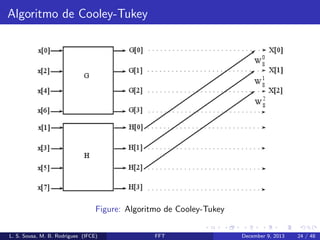
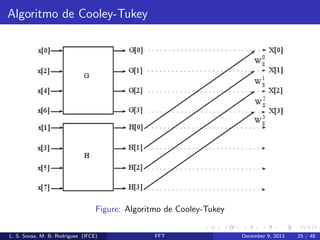
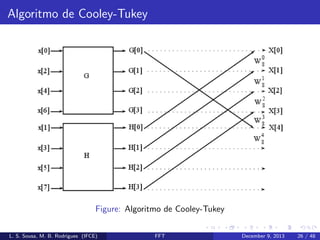
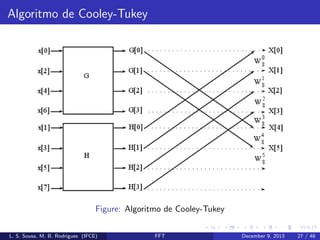
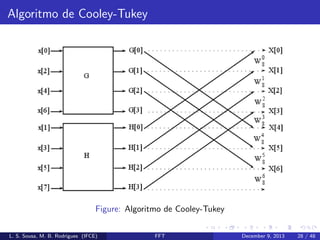
Cada parcela da equa¸˜o (11) ´ uma DFT de N/2 pontos:
ca
e
G[k] e H[k]
No caso de uma DFT de 8 pontos, o resultado da decima¸˜o no
ca
tempo gera o seguinte diagrama de fluxo.
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
20 / 48

21. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
21 / 48

22. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
22 / 48

23. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
23 / 48

24. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
24 / 48

25. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
25 / 48

26. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
26 / 48

27. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
27 / 48

28. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
28 / 48

29. Algoritmo de Cooley-Tukey
Figure: Algoritmo de Cooley-Tukey
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
29 / 48

30. Complexidade
An´lise de Complexidade:
a
DFT Cl´ssica
a
N 2 Multiplica¸˜es complexas e adi¸˜es.
co
co
Cooley-Tukey
k
X (k) = G [k] + WN H[k]
G [k] e H[k] s˜o duas DFTs de N/2 pontos, portanto, ambas realizam
a
2
(N/2) opera¸˜es.
co
k
A multiplica¸˜o WN H[k] ´ realizada N vezes.
ca
e
Assim, o custo do algoritmo de Cooley-Tukey ´ 2(N/2)2 + N.
e
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
30 / 48

31. Complexidade
Assim, usando o algoritmo de Cooley-Tukey, para N > 2, temos uma
complexidade menor do que usando o algoritmo de DFT cl´ssico.
a
Ainda podemos melhorar a complexidade se aplicarmos novamente a
ideia de divis˜o de Cooley-Tukey.
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
31 / 48

32. Complexidade
Figure: Divis˜o
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
32 / 48

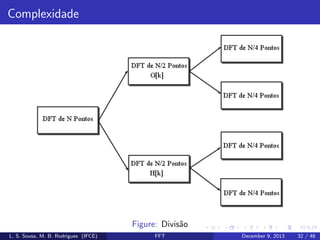
33. Algoritmo de Cooley-Tukey
Se N ´ potˆncia de 2, podemos dividir novamente o conjunto de
e
e
dados:
N/4−1
N/4−1
lk
g [2l]WN/4
G [k] =
+
k
WN/2
l=0
lk
h[2l + 1]WN/4
(13)
N/4−1
lk
h[2l]WN/4
+
k
WN/2
l=0
L. S. Sousa, M. B. Rodrigues (IFCE)
(12)
l=0
N/4−1
H[k] =
lk
g [2l + 1]WN/4
l=0
FFT
December 9, 2013
33 / 48

34. Algoritmo de Cooley-Tukey
G[k] = [ x[0], x[2], x[4], x[6] ], tal que
x[0] = 0, x[2] = 1, x[4] = 2, x[6] = 3
Figure: Divis˜o
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
34 / 48

35. Algoritmo de Cooley-Tukey
G[k] = [ x[0], x[2], x[4], x[6] ], tal que
x[0] = 0, x[2] = 1, x[4] = 2, x[6] = 3
Figure: Divis˜o
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
35 / 48

36. Algoritmo de Cooley-Tukey
G[k] = [ x[0], x[2], x[4], x[6] ], tal que
x[0] = 0, x[2] = 1, x[4] = 2, x[6] = 3
Figure: Divis˜o
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
36 / 48

37. Algoritmo de Cooley-Tukey
G[k] = [ x[0], x[2], x[4], x[6] ], tal que
x[0] = 0, x[2] = 1, x[4] = 2, x[6] = 3
Figure: Divis˜o
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
37 / 48

38. Algoritmo de Cooley-Tukey
G[k] = [ x[0], x[2], x[4], x[6] ], tal que
x[0] = 0, x[2] = 1, x[4] = 2, x[6] = 3
Figure: Divis˜o
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
38 / 48

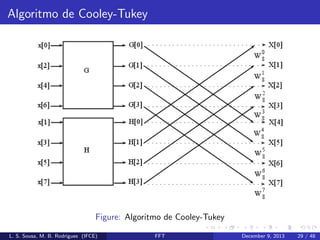
39. Algoritmo de Cooley-Tukey
G[k] = [ x[0], x[2], x[4], x[6] ], tal que
x[0] = 0, x[2] = 1, x[4] = 2, x[6] = 3
Figure: Fluxo Completo DFT 8 Pontos
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
39 / 48

40. An´lise da Complexidade
a
A equa¸˜o de recorrˆncia que descreve o problema ´
ca
e
e
T (n) = 2T (n/2) + O(n).
Aplicando o m´todo mestre, tempos que 2 = 21 , da´ temos que o
e
ı
custo ´ O(n log n).
e
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
40 / 48

41. Processo da Borboleta
A DFT de 8 pontos teve sua computa¸˜o reduzida at´ a DFT de 2
ca
e
pontos:
Figure: Butterfly
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
41 / 48

42. Processo da Borboleta
A obten¸˜o de um par de valores de um est´gio depende apenas de
ca
a
um par de valores do est´gio anterior.
a
Figure: Butterfly
N/2
Mas WN
= e −i(2π/N)N/2 = e −iπ = −1
r +(N/2)
Assim, o fator WN
pode ser escrito como:
r +(N/2)
WN
L. S. Sousa, M. B. Rodrigues (IFCE)
N/2
= WN
FFT
r
r
WN = −WN
(14)
December 9, 2013
42 / 48

43. Processo da Borboleta
Isso muda o gr´fico da borboleta para:
a
Figure: Gr´fico Butterfly Simplificado
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
43 / 48

44. Fluxo Completo FFT 8 pontos
Figure: Fluxo Completo FFT 8 Pontos
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
44 / 48

45. Fluxo Completo FFT 8 pontos
Figure: Fluxo Completo FFT 8 Pontos
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
45 / 48

46. Pseudoc´digo FFT
o
FFT(a, w)
se n = 1 ent˜o
a
retorne y = a
x = w 0 # x ir´ armazenar as potˆncias de w, ent˜o inicialmente x = 1.
a
e
a
# Etapa de divis˜o que separa ´
a
ındices pares e ´
ımpares
apar = [a0 , a2 , a4 , ..., an−2 ]
aimpar = [a1 , a3 , a5 , ..., an−2 ]
# Chamadas Recursivas, com W 2 como (n/2)-´sima raiz da unidade, pela
e
propriedade da redu¸˜o
ca
y par = FFT (apar , w 2 )
y impar = FFT (aimpar , w 2 )
# Etapa de combina¸˜o, usando x = w i
ca
para i = 0 a n/2-1 fa¸a
c
yi = yipar + xyiimpar #Usa a propriedade reflexiva
yi+n/2 = yipar − xyiimpar
x = xw
retorne y
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
46 / 48

47. MATLAB
Aplica¸˜o no MATLAB
ca
Barata exibir´ um exemplo no MATLAB da FFT em um sinal.
a
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
47 / 48

48. Referˆncias e Agradecimentos
e
Referˆncias
e
Centro de Inform´tica - UFPE - Carlos Alexandre Mello
a
Fundamentos da Matem´tica Elementar - Volume 6 - Gelson Iezzi
a
Discrete-Time Signal Processing, J.R.Buck,
A.Oppenheim e R.W.Schafer, Prentice-Hall,
1999
Agradecimentos
Obrigado pela aten¸˜o!
ca
L. S. Sousa, M. B. Rodrigues (IFCE)
FFT
December 9, 2013
48 / 48