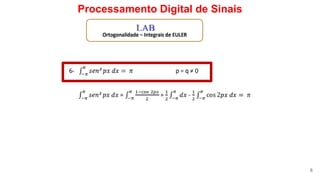
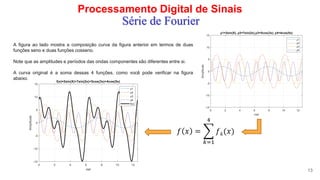
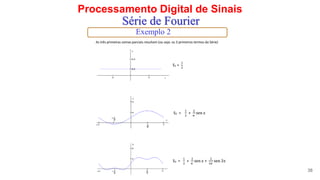
O documento discute a série de Fourier e como qualquer função periódica pode ser representada como uma soma de funções seno e cosseno. Apresenta exemplos de decomposições de funções em séries de Fourier, incluindo ondas quadradas deslocadas ao longo do eixo Y, e discute como o valor do coeficiente a0 está relacionado à posição da onda quadrada.