O documento apresenta um resumo sobre processamento digital de sinais. Aborda conceitos como sinais discretos no tempo, sistemas lineares e invariantes no tempo, transformada Z e transformada discreta de Fourier. Também discute técnicas de filtragem digital, processamento de imagens, áudio e voz.





![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 6
1. Processamento Digital de Sinais
Sinais estão presentes em diversas situações do dia-a-dia do ser humano. Um
sinal pode ser definido como uma função que carrega uma informação. A forma
mais comum para nós é a comunicação por sinal de voz. Nesse exemplo, temos
o sinal gerado pelo trato vocal e o sinal recebido pelo sistema auditivo. Apesar
de ser o mesmo sinal transmitido a forma como ele é processado é inerente ao
receptor. O processamento de sinais lida com a representação, transformação e
manipulação dos sinais e da informação que eles contêm. Até a década de 60, a
tecnologia para processamento de sinais era basicamente analógica. A evolução
de computadores e microprocessadores juntamente com diversos
desenvolvimentos teóricos causou um grande crescimento na tecnologia digital,
surgindo o processamento digital de sinais (PDS). Um aspecto fundamental do
processamento digital de sinais é que ele é baseado no processamento de
seqüências de amostras. Para tanto, o sinal contínuo no tempo é convertido
nessa seqüência de amostras, i.e., convertido em um sinal discreto no tempo.
Após o processamento digital, a seqüência de saída pode ser convertida de
volta a um sinal contínuo no tempo.
A maior parte do processamento de sinais envolve processar um sinal para obter
outro sinal. Normalmente, isso é conseguido por um processo conhecido como
filtragem.
Sinais podem ser classificados em quatro diferentes categorias dependendo de
carcaterísticas de tempo e dos tipos de valores que eles podem assumir. Sinais
contínuos no tempo (ou analógicos) são definidos para qualquer valor de tempo
e eles assumem valores no intervalo contínuo (a, b), onde a pode ser -∞ e b
pode ser +∞. Podem ser representados por uma função de variáveis contínuas.
Sinais discretos no tempo são definidos apenas para certos valores específicos
de tempo. Podem ser representados matematicamente por uma sequência de
números reais ou complexos, x. O n-ésimo número dessa seqüência é denotado
por x[n]. Assim, x é formalmente escrito como:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-6-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 7
x = {x[n]}, -∞ <n < ∞
onde n é um inteiro. Tais seqüências são geradas a partir de um processo de
amostragem periódica de um sinal analógico. Assim, o valor numérico do n-
ésimo número da seqüência é igual ao valor do sinal analógico xa(t) no tempo
nT, i.e.:
x[n] = xa(nT), -∞ <n < ∞
Os valores de amplitude de sinais contínuos ou discretos no tempo podem ser
contínuos ou discretos. Se um sinal pode assumir qualquer valor dentro de um
espaço finito ou infinito, ele é dito um sinal contínuo em valores. Sinais digitais
são aqueles para os quais tanto o tempo quanto a amplitude são discretos. Ou
seja, ele é discreto no tempo e só pode assumir valores dentro de um conjunto
finito de possíveis valores (é discreto em valores).
Sinais também podem ser classificados em determinísticos ou aleatórios.
Qualquer sinal que podem ser unicamente descrito por uma expressão
matemática, uma tabela de dados ou uma regra bem definida é chamado
determinístico. Esse termo é usado para destacar que quaisquer valores
passados, presentes e futuros do sinal são conhecidos precisamente, sem
incerteza. No entanto, em aplicações práticas, os sinais não podem ser
representados precisamente por equações matemáticas ou suas descrições são
muito complexas para uso. Isso indica que tais sinais têm comportamentos
imprevisíveis sendo chamados de sinais aleatórios.
1.1 Principais Tipos de Sinais
Em um estudo sobre processamento digital de sinais, alguns sinais são de mais
importância. Dentre eles, temos o impulso unitário, δ[n], definido como:
=
≠
=
0,1
0,0
][
n
n
nδ](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-7-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 8
Um dos mais importantes aspectos do impulso é que uma seqüência arbitrária
pode ser representada como uma soma de impulsos escalonados e deslocados.
Por exemplo, a seqüência p[n] abaixo:
pode ser representada como:
p[n] = 3.δ[n+3] + 2.δ[n + 1] + 4.δ[n - 2] – 1.δ[n – 3]
De forma mais geral, qualquer seqüência x[n] pode ser representada como:
∑
∞
−∞=
−=
k
knkxnx ][][][ δ
Outra seqüência importante é o degrau unitário, u[n]:
<
≥
=
0,0
0,1
][
n
n
nu
O degrau relaciona-se com o impulso como:
∑−∞=
=
n
k
knu ][][ δ
Uma forma alternativa de representar o degrau em termos de impulso é obtida
interpretando o degrau em termos de uma soma de impulsos deslocados. Isso
pode ser expresso como:
∑
∞
=
−=
0
][][
k
knnu δ
Por outro lado, o impulso relaciona-se com o degrau unitário como:
δ[n] = u[n] – u[n – 1]](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-8-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 9
Uma seqüência exponencial é importante na análise de sistemas discretos e
invariantes no tempo. A forma geral de uma seqüência exponencial é dada por:
x[n] = A.αn
1.2 Sistemas Discretos no Tempo
Um sistema discreto no tempo é definido matematicamente como uma
transformação que mapeia uma seqüência de entrada x[n] em uma seqüência
de saída y[n]. Isso pode ser denotado por:
y[n]=T{x[n]}
como representado na Fig. 1.1.
Fig. 1.1. Representação de um sistema discreto no tempo
Alguns exemplos ilustram sistemas simples:
1) Sistema de atraso ideal: y[n] = x[n – nd], -∞ <n < ∞
2) Média móvel: ∑−=
−
++
2
1
][
1
1
21
M
Mk
knx
MM
A seguir, destacamos algumas importantes propriedades dos sistemas.
1) Um sistema é dito sem memória (memoryless systems) se a saída y[n] a
cada valor de n depende apenas da entrada x[n] no mesmo valor de n.
Ex: y[n] = {x[n]}2
2) Um sistema é linear se obedece ao princípio da superposição. Ou seja:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-9-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 10
T{a.x1[n] + b.x2[n]} = a.T{x1[n]} + b.T{x2[n]}
Ex: Acumulador: ∑−∞=
=
n
k
kxny ][][
3) Um sistema é invariante no tempo é um sistema no qual um deslocamento
no tempo (ou atraso) da seqüência de entrada gera um deslocamento
correspondente na seqüência de saída. Ou seja, suponha um sistema que
transforma uma seqüência de entrada x[n] na seqüência de saída y[n]. Se a
seqüência de entrada sofre um deslocamento de n0, x[n] = x[n – n0], então a
seqüência de saída torna-se y[n] = y[n – n0].
Ex: Um sistema de atraso ideal é um sistema invariante no tempo.
Ex: O seguinte exemplo mostra um sistema que não é invariante no tempo:
y[n] = x[M.n], -∞ <n < ∞
4) Um sistema é dito causal se ele não depende de valores futuros da
seqüência. Ou seja, o valor de y[n1] pode ser calculado apenas com valores de
x[n] para n ≤ n1.
Ex: Um sistema não causal: y[n] = x[n + 1] – x[n]
5) Um sistema é dito estável se toda entrada limitada provoca uma saída
limitada. Assim, se, para todo n, |x[n]| ≤ B < ∞, para algum valor finito B, então
|y[n]| ≤ C < ∞, para algum valor finito C.
1.3 Sistemas Lineares e Invariantes no Tempo
Uma classe importante de sistemas consiste naqueles que são lineares e
invariantes no tempo. Como dito acima, os sistemas lineares são aqueles que
obedecem ao princípio da superposição. Se a propriedade da linearidade é](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-10-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 11
combinada com a representação de uma seqüência geral como uma
combinação de impulsos, então um sistema linear pode ser completamente
caracterizado pela sua resposta ao impulso. Seja hk[n] a resposta do sistema a
δ[n – k]. Assim, como:
∑
∞
−∞=
−=
k
knkxnx ][][][ δ
então
}][][{][ ∑
∞
−∞=
−=
k
knkxTny δ
Pelo princípio da superposição, podemos escrever:
∑∑
∞
−∞=
∞
−∞=
=−=
k
k
k
nhkxknTkxny ][][}][{][][ δ
De acordo com essa equação, a resposta do sistema a qualquer entrada pode
ser expressa em termos da resposta a δ[n – k].
A propriedade da invariância no tempo implica que, se h[n] é a resposta a δ[n],
então a resposta a δ[n - k] é h[n – k]. Com isso, podemos dizer que:
∑
∞
−∞=
−=
k
knhkxny ][][][ (Eq. 1.1)
Como conseqüência, um sistema linear invariante no tempo é completamente
descrito por sua resposta ao impulso. Essa equação é conhecida como soma de
convolução (convolution sum) que pode ser representada pela notação:
y[n] = x[n]*h[n] (Eq. 1.2)
Apesar da semelhança na notação, deve-se salientar que a soma de convolução
para sinais discretos não é uma aproximação da integral de convolução.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-11-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 12
Propriedades da soma de convolução:
1) Comutatividade:
x[n]*h[n] = h[n]*x[n]
Isso pode ser facilmente justificável com uma mudança de variável na Eq. 1.1.
Especificamente, podemos fazer m = n – k.
2) Distributividade:
x[n]*(h1[n] + h2[n]) = x[n]*h1[n] + x[n]*h2[n]
3) Conexão em Cascata
4) Conexão em Paralelo](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-12-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 13
5) Causalidade
Como definido anteriormente, um sistema é dito causal se sua resposta não
depende de eventos futuros. Ou seja, para calcular a saída de y[n0], precisamos
apenas de x[n], n ≤ n0. Isso implica na condição:
h[n] = 0, n < 0
Assim, para testar a causalidade basta testar se h[n] = 0 para n<0.
6) Estabilidade
A estabilidade é garantida se:
∞<= ∑
∞
−∞=n
nhS |][|
Para qualquer que seja a entrada x[n] de um sistema:
x[n]* δ[n] = x[n]
Assim, em geral, se um sistema linear invariante no tempo tem uma resposta ao
impulso h[n], então seu sistema inverso, se existir, tem resposta ao impulso hi[n]
definida pela relação:
h[n]*hi[n] = hi[n]*h[n] = δ[n]
Uma classe importante de sistemas lineares invariantes no tempo consiste
daqueles para os quais x[n] e y[n] se relacionam através de uma equação de
diferenças de coeficientes constantes lineares de n-ésima ordem da forma:
∑ ∑= =
−=−
N
k
M
k
kk knxbknya
0 0
][][ (Eq. 1.3)
Um exemplo de um tal sistema é um acumulador definido pela seqüência cujo
diagrama de blocos pode ser visto na figura abaixo:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-13-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 14
Tal sistema é representado pela equação de diferenças:
y[n] = y[n – 1] + x[n]
ou y[n] - y[n – 1] = x[n]
Pela Eq. 1.3, temos: N = 1, a0 = 1, a1 = -1, M = 0 e b0 = 1.
Assim, para cada valor de n a saída é dada pela entrada x[n] somada com o
valor anterior do acumulador, y[n – 1].
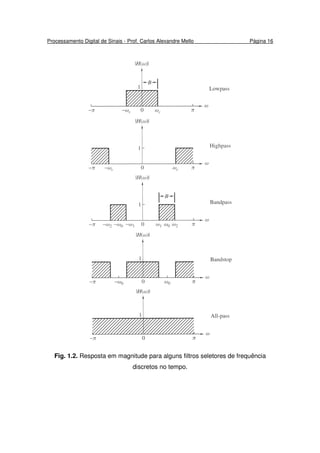
1.4 Sistemas LTI como Filtros Seletores de Frequência
O termo filtro é normalmente usado para descrever um dispositivo que
discrimina, de acordo com algum atributo do objeto aplicado como entrada, o
que passa através dele. Por exemplo, como um filtro de ar que deixa o ar
passar, mas retém partículas de impureza. Um sistema LTI também funciona
como um tipo de discriminante ou filtrando entre os vários componentes de
frequência na sua entrada. A forma da filtragem é definida pela resposta de
frequência H(ω) que depende da escolha de parâmetros do sistema (como os
coeficientes do filtro). Assim, com uma escolha apropriada de parâmetros,
podemos projetar filtros seletores de frequência que deixam passar sinais
contendo componentes de frequência em algumas bandas e atenuando sinais
contendo componentes de frequência em outras bandas.
Em geral, um sistema LTI modifica o espectro do sinal de entrada X(ω) de
acordo com a resposta em frequência H(ω) que leva a um sinal de saída com
espectro Y(ω) = H(ω)X(ω). De certa forma, H(ω) atua como uma função de peso
nos diferentes componentes de frequência do sinal de entrada. Assim, um](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-14-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 17
Outra característica de um filtro ideal é uma resposta de fase linear. Considere
que um sinal {x[n]} com componentes de frequência dentro da faixa de ω1< ω
<ω2 passa por um filtro com resposta em frequência:
<<
=
−
senão
Ce
H
nj
0
)( 21
0
ωωω
ω
ω
onde C e n0 são constantes. O sinal na saída do filtro terá um espectro:
0
)()()()( nj
eCXHXY ω
ωωωω −
==
Aplicando as propriedades da transformada de Fourier, obtemos a saída no
domínio do tempo:
Y[n] = C.x[n – n0]
Consequentemente, a saída do filtro é simplesmente uma versão escalonada e
atrasada do sinal de entrada. Tanto um atraso simples quanto uma diferença em
escala são considerados toleráveis e não distorções do sinal. Portanto, filtros
ideais têm uma característica de fase linear na banda de passagem que é:
Θ(ω) = -ωn0
A derivada da fase em relação à frequência é medida em unidades de atraso.
Assim, podemos definir o atraso do sinal como uma função da frequência como:
ω
ω
ωτ
d
d
g
)(
)(
Θ
−=
τg(ω) é chamado de atraso de grupo (group delay) do filtro. Entendemos τg(ω)
como o atraso de tempo que os componentes de frequência ω de um sinal são](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-17-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 18
submetidos à medida que ele passa da entrada à saída do sistema. Note que,
quando Θ(ω) é linear, τg(ω) = n0 = constante. Nesse caso, todas as componentes
de frequência do sinal de entrada sofrem o mesmo atraso de tempo.
Como conclusão, todos os filtros ideais têm características de magnitude
constante e fase linear dentro da banda de passagem. Em todos os casos, tais
filtros não são fisicamente realizáveis, mas servem como idealizações
matemáticas para filtros práticos.
1.5 Representação de Sequências pela Transformada de Fourier
Assim como sinais do contínuo, os sinais discretos no tempo também podem ser
representados de formas diferentes. Uma das formas mais utilizadas é através
da transformação do sinal para o domínio da freqüência através da
Transformada de Fourier. Muitas seqüências podem ser representadas por uma
integral de Fourier da forma:
∫−
=
π
π
ωω
ω
π
deeXnx njj
)(
2
1
][
(Eq. 1.4)
onde X(ejw
) é dada por:
∑
∞
−∞=
−
=
n
njj
enxeX ωω
][)(
(Eq. 1.5)
A Eq. 1.4 é conhecida como a Transformada Inversa de Fourier, enquanto a Eq.
1.5 é a Transformada de Fourier.
Em geral, a Transformada de Fourier é uma função complexa em ω. Como na
resposta à freqüência, algumas vezes, pode-se expressar X(ejω
) na forma:
X(ejω
) = XR(ejω
) + j.XI(ejω
)](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-18-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 19
ou na forma polar:
X(ejω
) = |X(ejω
)| ej∠X(e^jω)
As quantidades |X(ejω
)| e ∠X(ejω
) são chamadas de magnitude e fase da
Transformada de Fourier (também chamada de espectro de Fourier ou,
simplesmente, espectro).
Há casos onde a Transformada de Fourier para uma dada seqüência não
converge. Esses casos podem ser definidos através da Transformada Z como
veremos posteriormente.
Podemos verificar facilmente que as Eqs. 1.4 e 1.5 são inversas realmente.
Especificamente, considere:
^
][][
2
1
nxdeemx nj
m
mj
=
∫ ∑
−
∞
−∞=
−
π
π
ωω
ω
π
Se trocarmos a ordem da integração com o somatório, temos:
= ∫∑
−
−
∞
−∞=
π
π
ω
ω
π
demxnx mnj
m
)(
^
2
1
][][
Calculando a integral dentro dos parênteses, temos:
≠
=
=
−
−
=∫−
−
nm
nm
mn
mn
de mnj
,0
,1
)(
))(sin(
2
1 )(
π
π
ω
π
π
π
ω
][ mn −= δ](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-19-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 20
Assim:
][][][][
^
nxmnmxnx
m
=−= ∑
∞
−∞=
δ
Exemplo 1:
Seja x[n] = an
u[n].
A TF é dada por:
∑ ∑∑
∞
=
−
∞
=
−−
∞
−∞=
−
−
====
0 0 1
1
)(][)(
n
jw
n
njwjwnn
n
jwnjw
ae
aeeaenxeX
Que converge se |a.e-jw
| < 1 ou |a| < 1.
OBS:
α
α
−
→∑
∞
= 1
1
0n
n
, para |α| < 1
Exemplo 2:
Vamos calcular a resposta ao impulso de um filtro passa-baixa ideal cuja
resposta em freqüência é:
<<
<
=
π||,0
||,1
)(
ww
ww
eH
c
cjw
LPF
A resposta o impulso hLPF[n] pode ser encontrada através da Transformada
Inversa de Fourier:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-20-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 21
∫∫ −−
==
c
c
w
w
jwnjwnjw
LPFLPF dwedweeHnh
ππ
π
π 2
1
)(
2
1
][
∞<<−∞= n
n
nw
nh c
LPF ,
)sin(
][
π
1.5.1 Propriedades da Transformada de Fourier
Algumas propriedades da TF: Seja: x[n] ↔ X(ejw
) e y[n] ↔ Y(ejw
)
Propriedade Seqüência Transformada de Fourier
Linearidade a.x[n] + b.y[n] a.X(ejw
) + b.Y(ejw
)
Deslocamento no Tempo x[n – nd] e-jwnd
X(ejw
)
Deslocamento na Freq ejwon
x[n] X(ej(w – w0)
)
Reverso no Tempo x[-n]
X(e-jw
)
X*(e-jw
), se x[n] é real
Diferenciação em Freq n.x[n] j dX(ejw
)/dw
Convolução x[n]*y[n] X(e-jw
).Y(e-jw
)
Modulação x[n].y[n]
∫−
−
π
π
θθ
θ
π
deYeX wjj
)()(
2
1 )(](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-21-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 22
1.6 Códigos do MatLab
Função Impulso
function [x, n] = impseq(n0, n1, n2) % Impulso
n = [n1:n2];
x = [(n-n0) == 0];
stem (x);
Exemplos:
1.
>> impseq (5, 0, 10);
2.
x[n] = 2.δ[n + 2] - δ[n – 4], -5 ≤ n ≤ 5
>> n = [-5:5];
>> x = 2*impseq(-2, -5,5) - impseq(4, -5, 5);
>> stem (n, x); title ('Exemplo de Sequencia'); xlabel('n'); ylabel('x[n]');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-22-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 23
Função Degrau
function [x, n] = stepseq(n0, n1, n2) % Degrau
n = [n1:n2];
x = [(n-n0) >= 0];
stem (x);
Exemplos
1.
>> stepseq (5, 0, 10);
2.
x[n] = n[u[n] – u[n – 10]] + 10e-0.3(n – 10)
[u[n – 10] – u[n – 20]], 0 ≤ n ≤ 20
>> n = 0:20;
>> x1 = n.*(stepseq(0,0,20) - stepseq(10,0,20));
>> x2 = 10*exp(-0.3*(n-10)).*(stepseq(10,0,20) - stepseq(20,0,20));
>> x = x1 + x2;
>> stem(n,x); title('Sequencia de Degraus'); xlabel('n'); ylabel ('x[n]');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-23-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 24
Senóide
function x = sinseq(n1,n2) % Senóide
n = [n1:0.1:n2];
x = 3*cos(0.1*pi*n + pi/3) + 2*sin(0.5*pi*n);
stem (x);
Exemplo:
>> sinseq (0, 10);
Operações em sequências
Adição de sinais
y[n] = x1[n] + x2[n]
function [y,n] = sigadd(x1,n1,x2,n2)
n = min(min(n1),min(n2)):max(max(n1),max(n2));
y1 = zeros(1, length(n));
y2 = y1;
y1(find((n>=min(n1))&(n<=max(n1))==1)) = x1;
y2(find((n>=min(n2))&(n<=max(n2))==1)) = x2;
y = y1 + y2;
Multiplicação de sinais
y[n] = x1[n].x2[n]
function [y,n] = sigmult(x1,n1,x2,n2)
n = min(min(n1),min(n2)):max(max(n1),max(n2));
y1 = zeros(1, length(n));
y2 = y1;
y1(find((n>=min(n1))&(n<=max(n1))==1)) = x1;
y2(find((n>=min(n2))&(n<=max(n2))==1)) = x2;
y = y1.*y2;](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-24-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 25
Deslocamento
y[n] = x[n – k]
function [y,n] = sigshift(x, m, n0)
n = m + n0;
y = x;
Inversão
y[n] = x[-n]
function [y,n] = sigfold(x,n)
y = fliplr(x);
n = -fliplr(n);
Exemplo: Seja x[n] = {1, 2, 3, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1}. O valor em negrito
corresponde ao centro da sequência.
Sobre as sequências, temos que:
>> n = -2:10;
>> x = [1:7, 6:-1:1];
a) Plote x1[n] = 2x(n – 5) – 3x[n + 4].
>> [x11, n11] = sigshift(x, n, 5);
>> [x12, n12] = sigshift(x, n, -4);
>> [x1, n1] = sigadd(2*x11,n11,-3*x12, n12);
>> stem (n1, x1); title(‘Sequencia’); xlabel (‘n’); ylabel (‘x1(n)’);](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-25-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 26
b) Plote x2[n] = x[3 – n] + x[n].x[n – 2]
>> [x21, n21] = sigfold(x, n);
>> [x21, n21] = sigshift(x21, n21,3);
>> [x22, n22] = sigshift(x, n,2);
>> [x22, n22] = sigmult(x, n, x22, n22);
>> [x2, n2] = sigadd(x21, n21, x22, n22);
>> stem (n2, x2); title('Sequencia');
>> xlabel ('n'); ylabel ('x2(n)');
Convolução
Considere as sequências:
x = [3, 11, 7, 0, -1, 4, 2], -3 ≤ n ≤ 3
h = [2, 3, 0, -5, 2, 1]; -1 ≤ n ≤ 4
onde, novamente, os termos em negrito indicam a origem do eixo das abscissas.
As sequências podem ser vistas abaixo:
x[n] h[n]](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-26-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 27
Podemos usar a função conv do MatLab diretamente:
>> x = [3, 11, 7, 0, -1, 4, 2];
>> h = [2, 3, 0, -5, 2, 1];
>> y = conv (x, h);
y = 6 31 47 6 -51 -5 41 18 -22 -3 8 2
O problema do uso da função conv é que não sabemos, na resposta, onde está
a origem da sequência. Para tanto, vamos criar uma nova função:
function [y, ny] = conv_m (x, nx, h, nh)
nyb = nx(1) + nh(1);
nye = nx(length(x)) + nh(length(h));
ny = [nyb:nye];
y = conv(h, x);
>> x = [3, 11, 7, 0, -1, 4, 2];
>> nx = [-3:3];
>> h = [2, 3, 0, -5, 2, 1];
>> nh = [-1:4];
>> [y, ny] = conv_m (x, nx, h, nh)
y = 6 31 47 6 -51 -5 41 18 -22 -3 8 2
ny = -4 -3 -2 -1 0 1 2 3 4 5 6 7
A amplitude -51 está no ponto de origem (ny = 0).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-27-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 28
Equações de Diferenças e Resposta ao Impulso
Exemplo: Dada a seguinte equação de diferenças:
y[n] – y[n – 1] + 0.9y[n – 2] = x[n], para todo n
a) Calcule e plote sua resposta ao impulso h[n] para n = -20,.., 100.
Como vimos anteriormente, uma equação de diferenças é da forma:
∑ ∑= =
−=−
N
k
M
k
kk knxbknya
0 0
][][
De acordo com a equação dada, temos:
a = [1, -1, 0.9] e b = [1]
No MatLab, fazemos:
>> x = impseq(0, -20, 120);
>> n = [-20:120];
>> h = filter(b, a, x);
>> stem(n, h); title('Resposta ao impulso'); xlabel('n'); ylabel('h[n]');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-28-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 29
b) Calcule e plote sua resposta ao degrau s[n] para n = -20,.., 100.
No MatLab, fazemos:
>> x = stepseq(0, -20, 120);
>> n = [-20:120];
>> h = filter(b, a, x);
>> stem(n, h); title('Resposta ao degrau'); xlabel('n'); ylabel('s[n]');
c) O sistema é estável?
Como vimos, um sistema é estável se:
∞<= ∑
∞
−∞=n
nhS |][|
Assim, no MatLab, basta fazermos:
>> sum(abs(h))
Ans = 14.8785
Logo, o sistema é estável.
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-29-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 30
1.7 Exercícios
1. Considere um sistema linear arbitrário com entrada x[n] e saída y[n]. Mostre
que se x[n] = 0 para todo n, então y[n] deve ser zero para todo n também.
2. Usando a definição de linearidade, mostre que o sistema de atraso ideal e a
média móvel são ambos lineares.
3. Para cada sistema abaixo, determine se ele é (1) estável, (2) causal, (3)
linear, (4) invariante no tempo e (5) sem memória:
a. T(x[n]) = g[n]x[n], com g[n] dado
b. T(x[n]) = Σn
k=n0 x[k]
c. T(x[n]) = x[n – n0]
d. T(x[n]) = exp(x[n])
e. T(x[n]) = a.x[n] + b, a e b números reais
f. T(x[n]) = x[-n])
g. T(x[n]) = x[n] + 3.u[n + 1]
4. O sistema T abaixo é invariante no tempo. Quando as entradas dele são
x1[n], x2[n] e x3[n], as saídas são y1[n], y2[n] e y3[n], respectivamente.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-30-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 31
a) Determine se o sistema pode ser linear.
b) Se a entrada x[n] do sistema é um impulso (δ[n]), qual a saída y[n]?
c) Determine a relação entre a entrada e a saída do sistema.
5. Para cada par de sequências abaixo, use convolução discreta para encontrar
a resposta à entrada x[n] do sistema linear invariante no tempo com resposta ao
impulso h[n].
a)
b)
6. Considere o sistema com entrada x[n] e saída y[n] que satisfaz a equação de
diferenças:
y[n] = n.y[n – 1] + x[n]
O sistema é causal tal que, se x[n] = 0, para n < 0, então y[n] = 0, para n < 0.
a) Se x[n] = δ[n], determine y[n] para todo n.
b) O sistema é linear?
c) O sistema é invariante no tempo?](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-31-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 32
7. Plote a seguintes sequências no MatLab:
a) x[n] = n2
.(u[n + 5] – u[n – 6]) + 10.δ[n], -5 ≤ n ≤ 5
b) x[n] = 20.(0,5)n
.(u[n – 4] – u[n - 10]), -5 ≤ n ≤ 5
8. Seja x[n] = {1, -2, 4, 6, -5, 8, 10}, gere e plote no MatLab as seguintes
sequências:
a) x[n] = 3.x[n + 2] + x[n – 4] – 2.x[n]
b) x[n] = 5.x[5 + n] + 4.x[n + 4] + 3.x[n]
9. Usando as seguintes sequências:
x1[n] = u[n + 10] – u[n – 20] x2[n] = 2.δ[n – 2] + 5.u[n + 10]
x3[n] = 5.u[n + 2] – 6.u[n – 3]
mostre que a convolução linear tem as seguintes propriedades como válidas:
Comutatividade: x1[n]*x2[n] = x2[n]*x1[n]
Associatividade: (x1[n]*x2[n])*x3[n] = x1[n]*(x2[n]*x3[n])
Distributividade: x1[n]*(x2[n] + x3[n]) = x1[n]*x2[n] + x1[n]*x3[n])
Identidade: x[n]* δ[n – n0] = x[n – n0]
Use a função conv_m.m apresentada anteriormente.
10. A operação de dilatação de sinal (ou decimação ou downsampling) é
definida por:
y[n] = x[nM]
na qual a sequência de entrada é down-sampled por um fator inteiro M. Por
exemplo, se :
x[n] = {...., -2, 4, 3, -6, 5, -1, 8,...}
então a sequência down-sampled por um fator de 2 é dada por:
y[n] = {..., -2, 3, 5, 8, ..}
Escreva uma função no MatLab que execute essa dilatação. A função deve ser
da forma:
function [y, n] = dnsample(x, n, M)
Cuidado com a origem do eixo!! ](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-32-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 34
2. A Transformada Z
A Transformada Z (TZ) é uma ferramenta matemática poderosa para análise de
sinais e sistemas. A transformada Z constitui a forma discreta da transformada
de Laplace. Seja a Transformada de Fourier (TF) de uma seqüência dada por:
∑
∞
−∞=
−
=
n
jwnjw
enxeX ][)(
Seja z = ejw
. Temos então, a TZ definida como:
∑
∞
−∞=
−
=
n
n
znxzX ][)(
Essa é chamada também de TZ bilateral. A transformada unilateral é dada por:
∑
∞
=
−
=
0
][)(
n
n
znxzX
Notadamente, há uma relação entre a TZ e a TF. Se z é uma variável complexa,
z pode ser escrita como ejw
= cos(w) + j.sen(w). Nesse caso, a TZ transforma-se
na TF. De forma mais geral, se z = r.ejw
, sua representação gráfica corresponde
ao círculo no Plano imaginário (chamado de Plano-Z). Se esse círculo tem raio
igual a 1, então temos a condição da TZ = TF (Fig. 2.1). Assim, a TZ calculada
no círculo unitário é igual à TF.
A Transformada Z não converge para todos os valores de Z. Onde a TZ
converge é chamada de região de convergência (ROC – Region of
Convergence). Para garantir a convergência é preciso que:
∞<∑
∞
=
−
0
|][|
n
n
znx
Assim, é possível que TZ convirja mesmo se a TF não convergir. Para a TF
convergir, a ROC da TZ deve conter o círculo unitário. Uma transformada Z só
está completamente definida se sua ROC estiver determinada.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-34-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 36
2.1 Propriedades da Transformada Z
a) Linearidade: ax1[n] + bx2[n] ↔ aX1(z) + bX2(z), ROC = ROCx1∩ ROCx2
Comentários:
A prova de tal propriedade vem diretamente da definição de transformada Z:
∑
∞
−∞=
−
=
n
n
znxzX ][)(
Considere que x[n] = ax1[n] + bx2[n]. Logo:
=+=+= ∑∑
∞
−∞=
−−
∞
−∞=
−
n
nn
n
n
znbxznaxznbxnaxzX ][][])[][()( 2121
∑∑∑∑
∞
−∞=
−
∞
−∞=
−
∞
−∞=
−
∞
−∞=
−
+=+=
n
n
n
n
n
n
n
n
znxbznxaznbxznax ][][][][ 2121
= aX1(z) + bX2(z)
b) Deslocamento no tempo: x[n + n0] ↔ zn
0.X(z), ROC = ROCx (cuidado deve ser
tomado observando o que acontece para z = 0 ou z = ∞).
Comentários:
Suponha que y[n] = x[n – n0]. Logo:
∑
∞
−∞=
−
−=
n
n
znnxzY ][)( 0
Fazendo m = n – n0:
∑∑∑
∞
−∞=
−−
∞
−∞=
−−
∞
−∞=
+−
===
m
mn
m
nm
m
nm
zmxzzzmxzmxzY ][..][][)( 000 )(
)(.)( 0
zXzzY n−
=](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-36-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 37
c) Multiplicação por uma exponencial discreta: an
x[n] ↔ X(z/a), ROC = |a|ROCX
Comentários:
Essa propriedade é observável substituindo an
x[n] na definição de TZ:
∑∑
∞
−∞=
−
∞
−∞=
−
==
n
nn
n
n
znxaznxzX ][][)(
Como conseqüência disso, todas as posições de pólos e zeros são escalonadas
por um fator de a, já que, se X(z) tiver um pólo em z = z1, X(a-1
z) terá um pólo
em z = a.z1. Se a for um número real, essa propriedade pode ser entendida
como uma compressão ou expansão do plano Z.
d) Convolução no tempo: x1[n]*x2[n] ↔ X1(z).X2(z) , ROC contém ROCx1∩ ROCx2
Comentários:
Seja:
∑
∞
−∞=
−=
k
knxkxny ][][][ 21
Tal que:
∑
∞
−∞=
−
=
n
n
znyzY ][)(
∑ ∑
∞
−∞=
−
∞
−∞=
−=
n
n
k
zknxkx ][][ 21
Se mudarmos a ordem dos somatórios:
∑ ∑
∞
−∞=
∞
−∞=
−
−=
k n
n
zknxkxzY ][][)( 21
Fazendo no segundo somatório m = n – k, temos:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-37-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 38
∑ ∑
∞
−∞=
−
∞
−∞=
−
=
k
k
m
m
zzmxkxzY ][][)( 21
Assim, para valores de z dentro das regiões de convergência para X1(z) e X2(z),
podemos escrever:
)()()( 21 zXzXzY =
e) Diferenciação no Domínio Z: n.x[n] ↔ -z.dX(z)/dz, ROC = ROCx (cuidado
deve ser tomado observando o que acontece para z = 0 ou z = ∞).
Comentários:
Essa propriedade pode ser facilmente provada diferenciando a definição da TZ:
∑
∞
−∞=
−
=
n
n
znxzX ][)(
∑
∞
−∞=
−−
−=
n
n
znxn
zd
zdX 1
][)(
)(
)(
. (-z)
∑
∞
−∞=
−−
−−=−
n
n
znxnz
zd
zdX
z 1
][)(
)(
)(
∑
∞
−∞=
−
==−
n
n
nnxZznnx
zd
zdX
z ]}[{][
)(
)(
f) Reverso no tempo: x[-n] ↔ X(z-1
), ROC = 1/ROCX
Comentários:
Novamente, a definição de TZ prova esta propriedade:
∑
∞
−∞=
−
−=
n
n
znxzX ][)(
Fazendo m = -n, temos:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-38-320.jpg)
( 11 −
∞
−∞=
−−
∞
−∞=
=== ∑∑ zXzmxzmxzX
m
m
m
m
2.2 Pares de Transformadas Z
Segue um conjunto de pares de Transformadas Z mais úteis:
2.3 Exemplos de Cálculo da Transformada Z
A seguir, vamos apresentar alguns cálculos de transformada Z e como definir a
ROC.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-39-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 40
Exemplo 1: x[n] = an
u[n]
∑ ∑ ∑ ∑
∞
−∞=
∞
−∞=
∞
=
∞
=
−−−−
====
n n n n
nnnnnn
azzaznuaznxzX
0 0
1
)(][][)(
ROC:
|az-1
| < 1 ⇒ |z| > |a|
||||,
1
1
)()( 1
0
1
az
az
z
az
azzX
n
n
>
−
=
−
== −
∞
=
−
∑
Para a = 1:
1||,
1
1
)(][][ 1
>
−
=→←= −
z
z
zXnunx Z
Observamos que, para a = 1, a ROC não contém o círculo unitário. Logo, a TF
para essa seqüência não converge.
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-40-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 41
Exemplo 2: x[n] = -an
u[-n – 1]
∑∑∑
∞
−∞=
−
∞
−∞=
−
∞
−∞=
−
−−−=−−−==
n
nn
n
nn
n
n
znuaznuaznxzX ]1[]1[][)(
∑∑∑
∞
=
−
∞
=
−
−
−∞=
−
−=−=−=
0
1
1
1
)(1)(
n
n
n
nn
n
nn
zazazazX
ROC:
|a-1
z|<1 ⇒ |z|<|a|
||||,
1
1
1)(1)( 1
0
1
az
az
z
za
zazX
n
n
<
−
=
−
−=−= −
∞
=
−
∑
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-41-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 42
Exemplo 3: x[n] = (1/2)n
u[n] + (-1/3)n
u[n]
∑∑
∞
−∞=
−
∞
−∞=
−
−+
==
n
n
nn
n
n
znunuznxzX ][
3
1
][
2
1
][)(
∑∑
∞
−∞=
−
∞
−∞=
−
−+
=
n
n
n
n
n
n
znuznuzX ][
3
1
][
2
1
)(
∑∑
∞
=
−
∞
=
−
−+
=
00 3
1
2
1
)(
n
n
n
n
n
n
zzzX
∑∑
∞
=
−
∞
=
−
−+
=
0
1
0
1
3
1
2
1
)(
n
n
n
n
zzzX
(i) (ii)
ROC(i) = |(1/2).z-1
| < 1 ⇒ |z| > 1/2
ROC(ii) = |(-1/3).z-1
| < 1 ⇒ |z| > 1/3
ROC = ROC(i) ∩ ROC(ii) = |z| > 1/2
11
3
1
1
1
2
1
1
1
)(
−−
+
+
−
=
zz
zX
Para X(z), os pólos são dados por z=1/2 e z=-1/3 e os zeros são z=0 e z=1/12.
Uma das propriedades da ROC que podemos observar aqui é que os pólos não
fazem parte dela. ](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-42-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 43
Exemplo 4: x[n] = (-1/3)n
u[n] – (1/2)n
u[-n – 1]
∑∑
∞
−∞=
−
∞
−∞=
−
−−
−
−==
n
n
nn
n
n
znunuznxzX ]1[
2
1
][
3
1
][)(
∑∑
∞
−∞=
−
∞
−∞=
−
−−
−
−=
n
n
n
n
n
n
znuznuzX ]1[
2
1
][
3
1
)(
∑∑
−
−∞=
−
∞
=
−
−
−=
1
0 2
1
3
1
)(
n
n
n
n
n
n
zzzX
∑∑
∞
=
−∞
=
−
−
−=
10 2
1
3
1
)(
n
n
n
n
n
n
zzzX
∑∑
∞
=
−∞
=
−
−+
−=
0
1
0
1
2
1
1
3
1
)(
n
n
n
n
zzzX
(i) (ii)
ROC(i) = |(-1/3).z-1
| < 1 ⇒ |z| > 1/3
ROC(ii) = |(1/2)-1
.z| < 1 ⇒ |z| < 1/2
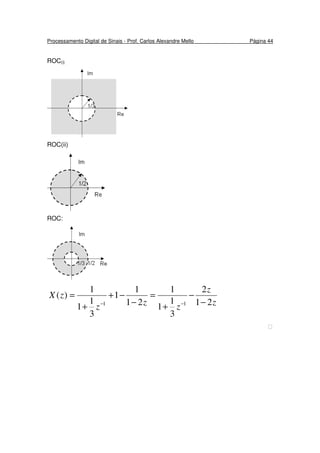
ROC = ROC(i) ∩ ROC(ii) = 1/3 < |z| < 1/2](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-43-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 45
Exemplo 5:
Função delta δ[n]: δ[n] = 0, n ≠ 0, e δ[n] = 1, n = 0
Transformada Z:
∑
∞
−∞=
−
===
n
n
zznxzX 1.1][)( 0
ROC = Todo o Plano Z
Exemplo 6: x[n] = δ[n – n0]
∑∑
∞
−∞=
−−
∞
−∞=
−
=−==
n
nn
n
n
zznnznxzX 0
][][)( 0δ
ROC = Todo o Plano Z.
Nos exemplos 5 e 6, x(n) é finita. X(z) é um polinômio de base z-1
e todo o plano
Z menos quando z = 0. Nesse ponto, a transformada não é definida.
Exemplo 7: Determine a transformada Z da sequência:
x[n] = (n – 2).(0,5)(n-2)
cos[π(n – 2)/3]u[n – 2]
Considerando a propriedade do deslocamento no tempo (x[n + n0] ↔ zn
0.X(z)),
temos:
X(z) = Z{x[n]} = z-2
.Z{n(0,5)n
.cos(πn/3)u[n]}
Considerando agora a diferenciação no domínio Z (n.x[n] ↔ -z.dX(z)/dz), temos:
X(z) = Z{x[n]} = z-2
.{-z.[d(Z{(0,5)n
.cos(πn/3).u[n]}/dz}
A transformada Z de (0,5)n
.cos(πn/3).u[n] é, pela tabela da Seção 2.2:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-45-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 46
21
1
25,0)
3
cos.5,0(21
)
3
cos.5,0(1
]][)
3
cos()5,0[(
−−
−
+−
−
=
zz
z
nu
n
z n
π
π
π
21
1
25,05,01
25,01
]][)
3
cos()5,0[( −−
−
+−
−
=
zz
z
nu
n
z n π
, ROC = |z| > 0,5
Assim:
+−
−
−= −−
−
−
21
1
1
25,05,01
25,01
)(
zz
z
dz
d
zzX
4321
543
0625,025,075,01
0625,05,025,0
)( −−−−
−−−
+−+−
+−
=
zzzz
zzz
zX ROC = |z| > 0,5
O seguinte procedimento no MatLab pode ajudar a verificar se a transformada
está correta. Para tanto, vamos calcular as primeiras 8 amostras da sequência
x[n] correspondente a X(z):
>> b = [0, 0, 0, 0.25, -0.5, 0.0625];
>> a = [1, -1, 0.75, -0.25, 0.0625];
>> [delta, n] = impseq(0,0,7)
delta =
1 0 0 0 0 0 0 0
n =
0 1 2 3 4 5 6 7
>> x = filter(b, a, delta) % checar a sequência
x =
0 0 0 0.2500 -0.2500 -0.3750 -0.1250 0.0781
>> x = [(n-2).*(1/2).^(n-2).*cos(pi*(n-2)/3)].*stepseq(2, 0, 7) % sequência original
x =
0 0 0 0.2500 -0.2500 -0.3750 -0.1250 0.0781
Conferindo com a sequência gerada pelo processo de filtragem.
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-46-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 47
2.4 Propriedades da Região de Convergência
A região de convergência (ROC) traz algumas propriedades:
1) A ROC é um anel ou disco no Plano Z com centro na origem.
2) A TF da seqüência x[n] converge absolutamente se e somente se a ROC da
TZ contém o círculo unitário.
3) A ROC não pode conter pólos.
4) Se x[n] é uma seqüência de duração finita, a ROC é todo plano Z.
5) Se x[n] é causal (right-sided), a ROC extende-se para além dos pólos mais
externos, possivelmente tendendo a infinito.
6) Se x[n] é não causal (left-sided), a ROC extende-se para uma região menor
que o menor pólo até zero.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-47-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 48
7) Se x[n] é uma seqüência com componentes parte causal e parte não-causal,
então a ROC é um anel.
8) A ROC é uma região conectada.
2.5 A Transformada Z Inversa
O cálculo da TZ inversa não é tão direto quanto o da TF. Aqui, existem diversas
maneiras formais e informais de calcular a TZ inversa dada uma expressão
algébrica e a ROC associada.
Seja a Transformada Z definida por:
∑
∞
−∞=
−
=
n
n
znxzX ][)(
Suponha que multiplicamos ambos os lados da transformada por zk-1
e
integremos os dois lados sobre um contorno fechado dentro da ROC de X(z) que
inclui a origem. Tal contorno pode ser visto na Figura 2.2. Assim, temos:
∫ ∫ ∑
∞
−∞=
−−−
=
C C n
nkk
dzznxdzzzX 11
][)(
(1)
onde C denota o contorno fechado na ROC de X(z), tomado no sentido anti-
horário. Como a série converge nesse contorno, podemos mudar a ordem da
integração e do somatório no lado direito, ficando com:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-48-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 49
∫ ∑ ∫
∞
−∞=
−−−
=
C n C
nkk
dzznxdzzzX 11
][)(
(2)
Pelo teorema de integração de Cauchy:
≠
=
=∫
−−
kn
kn
dzz
j C
nk
,0
,1
2
1 1
π (3)
onde C é qualquer contorno que inclui a origem. Aplicando (3), o lado direito de
(2) reduz-se a 2πj.x[k] e assim a fórmula inversa é alcançada:
∫
−
=
C
k
dzzzX
j
kx 1
)(
2
1
][
π (4)
Fig. 2.2. Contorno C para a integral da transformada Z inversa.
Essa é a inversa da transformada Z para uma dada seqüência. No entanto, nós
não precisaremos usar essa inversão já que dentro de sinais e sistemas, as
transformadas Z são funções racionais (i.e., razão entre dois polinômios). Para](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-49-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 50
tais transformadas, há métodos mais simples de inversão que envolvem tabelas
conhecidas e métodos mais simples. Os principais métodos são:
- Método da inspeção
- Expansão em Frações Parciais
- Expansão em Séries de Potências
O método da inspeção é o mais simples e consiste em apenas observar a
transformada e ver se ela é da forma de alguma TZ conhecida. Por exemplo,
dado:
1
2
1
1
1
)(
−
−
=
z
zX
, |z|> ½
Por observação, sabemos que:
x[n] = -(½)n
u[-n – 1]
Notadamente, o método da inspeção não é o mais apropriado para calcular TZs
inversas mais complexas.
Para ver como obter uma expansão em frações parciais, vamos assumir que
X(z) pode ser expressa como uma razão de polinômios em z-1
, i.e.,
∑
∑
=
−
=
−
= N
k
k
k
M
k
k
k
za
zb
zX
0
0
)(
Para calcular a transformada inversa, tentamos expressar X(z) da forma:
∑∑ =
−
−
=
−
−
+=
N
k k
k
NM
r
r
r
zd
A
zBzX
1
1
0 1
)(](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-50-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 52
2
2
1
2
3
210 =−−− AAB
21
2
1
00 =⇒= BB
Com isso, ficamos com:
−=+
−=+
⇒
=−−−
=++
5
2
1
1
2
2
1
3
12
21
21
21
21
AA
AA
AA
AA
Resolvendo, temos:
A1 = -9 e A2 = 8
Logo:
1
1 1
8
2
1
1
9
2)( −
− −
+
−
−
+=
zz
zX
que corresponde à Transformada Z da sequência:
][.8][)
2
1
.(9][2][ nununnx n
+−= δ
A expansão em série de potências é aplicada quando a transformada Z é um
polinômio da forma:
∑
∞
−∞=
−
=
n
n
znxzX ][)(
Isso ocorre, principalmente, se a TZ é uma seqüência finita.
Por exemplo, considere que a TZ de uma seqüência x[n] é da forma:
)1)(1)(
2
1
1()( 1112 −−−
−+−= zzzzzX](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-52-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 53
Uma expansão em frações parciais para esse caso não é apropriada. No
entanto, efetuando os produtos, podemos reduzir a expressão a:
12
2
1
1
2
1
)( −
+−−= zzzzX
que equivale à seqüência:
x[n] = δ[n + 2] – ½.δ[n + 1] - δ[n] + ½.δ[n – 1]
Exemplo 9: Considere a função:
143
)( 2
+−
=
zz
z
zX
Primeiro, vamos re-arranjar X(z) tal que ela se torne uma função em potências
de z-1
:
21
1
21
1
43
0
43
)( −−
−
−−
−
+−
+
=
+−
=
zz
z
zz
z
zX
Usando o MatLab, temos1
:
>> b = [0 1];
>> a = [3 -4 1];
>> [R, p, C] = residuez(b, a)
R =
0.5000
-0.5000
p =
1.0000
0.3333
C = [ ]
1
Para mais informação sobre a função residuez, digite help residuez no MatLab.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-53-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 54
que corresponde a:
1
1
3
1
1
5,0
1
5,0
)(
−
−
−
−
−
=
z
z
zX
De maneira similar, podemos voltar à forma anterior:
>> [b, a] = residuez(R, p, C)
b =
-0.0000 0.3333
a =
1.0000 -1.3333 0.3333
que corresponde a:
21
1
21
1
21
1
43
0
43
3
1
3
4
1
3
1
0
)( −−
−
−−
−
−−
−
+−
+
=
+−
=
+−
+
=
zz
z
zz
z
zz
z
zX
como antes.
Exemplo 10: Calcule a transformada Z inversa de:
)9,01()9,01(
1
)( 121 −−
+−
=
zz
zX , |z|>0,9
Podemos calcular o polinômio no denominador assim como os resíduos usando
MatLab:
>> b = 1;
>> a = poly([-0.9 -0.9 0.9]) % calcula os coeficientes do polinômio que tem essas
raízes
a = 1.0000 0.9000 -0.8100 -0.7290](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-54-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 55
>> [R, p, C] = residuez(b, a)
R =
0.2500
0.2500 - 0.0000i
0.5000 + 0.0000i
p =
0.9000
-0.9000 + 0.0000i
-0.9000 - 0.0000i
C = [ ]
Isso significa que X(z) pode ser expandido em frações parciais como:
1211
9,01
25,0
)9,01(
5,0
9,01
25,0
)( −−−
+
+
−
+
−
=
zzz
zX , |z| > 0,9
121
1
1
9,01
25,0
)9,01(
9,0
9,0
5,0
9,01
25,0
)( −−
−
−
+
+
−
+
−
=
zz
z
z
z
zX , |z| > 0,9
que, de acordo com as propriedades da transformada Z e a tabela da Seção 2.2,
nos dá:
][)9,0(25,0]1[)9,0)(1(
9
5
][)9,0.(25,0][ 1
nununnunx nnn
−++++= +
Vamos tentar deixar todas as parcelas em função de u[n]. Para tanto, vamos
trabalhar na segunda parcela:
]1[)9,0)(1(
9
5 1
++ +
nun n
Observe que: a.u[n + 1] = a.u[n = -1] + a.u[n]. Logo:
][)9,0)(1(
9
5
)9,0)(1(
9
5
]1[)9,0)(1(
9
5 1
1
11
nunnnun n
n
nn +
−=
++
+++=++
][)9,0)(1(
9
5
]1[)9,0)(1(
9
5 11
nunnun nn ++
+=++](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-55-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 56
][)9,0)(1(5,0][)9,0.(9,0).1(
9
5
nunnun nn
+=+=
][)9,0(5,0][)9,0(5,0 nunun nn
+=
Logo:
][)9,0(25,0][)9,0.(5,0][)9,0.(75,0][ nununnunx nnn
−++=
Como antes, podemos verificar as 8 primeiras amostras da sequência x[n], no
MatLab:
>> [delta, n] = impseq(0,0,7);
>> x = filter (b, a, delta)
x = 1.0000 0.9000 1.6200 1.4580 1.9683 1.7715 2.1258 1.9132
>> x = 0.75*(0.9).^n+0.5*n.*(0.9).^n + 0.25*(-0.9).^n
x = 1.0000 0.9000 1.6200 1.4580 1.9683 1.7715 2.1258 1.9132
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-56-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 57
2.6 Exercícios
1. Calcule a transformada Z das sequências:
a. x[n] = -(1/2)n
u[-n – 1]
b. y[n] = (-1/2)n
u[n] + (1/3)n
u[-n – 1]
c. y[n] =2δ[n – 3] + (-1/4)n
u[-n - 1] + (1/2)n
u[n]
2. Calcule a transformada Z das seguintes sequências usando as suas
propriedades e a tabela da Seção 2.2 e verifique seus resultados usando
MatLab.
a. x[n] = 2.δ[n-2] + 3u[n – 3]
b. x[n] = (1/3)n
u[n – 2] + (0,9)n-3
u[n]
3. Seja x[n] uma sequência com transformada Z dada por X(z). O que se pode
dizer sobre as sequências que geram as seguintes transformadas:
a. X1(z) = [(z – 1)/z]X(z)
b. X2(z) = z.X(z-1
)
4. Ache a transformada inversa de:
a.
1
2
1
1
1
)(
−
+
=
z
zX , ROC = |z| > ½
b.
1
2
1
1
1
)(
−
+
=
z
zX , ROC = |z| < 1/2
c.
21
1
8
1
4
3
1
2
1
1
)(
−−
−
++
−
=
zz
z
zX , ROC = |z| > 1/2](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-57-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 58
5. Determine a transformada inversa usando o método de expansão em frações
parciais de:
321
321
1
4
1
8
13
4
11
1
441
)(
−−−
−−−
−+−
+−−
=
zzz
zzz
zX
sabendo que a sequência é causal.
6. Suponha que X(z) é:
21
1
1
81,01
32
)( −−
−
+−
+
=
zz
z
zX , |z| > 0,9
Encontre as primeiras 20 amostras de x[n], usando o MatLab.
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-58-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 60
3. Teoria da Amostragem
Sinais discretos no tempo podem ser gerados de diferentes formas, mas a mais
comum é sendo uma representação de sinais contínuos no tempo. Em parte,
isso é devido ao fato que o processamento de sinais contínuos no tempo é feito
através do processamento discreto no tempo de seqüências obtidas através de
amostragem. Um sinal contínuo no tempo pode ser representado por amostras
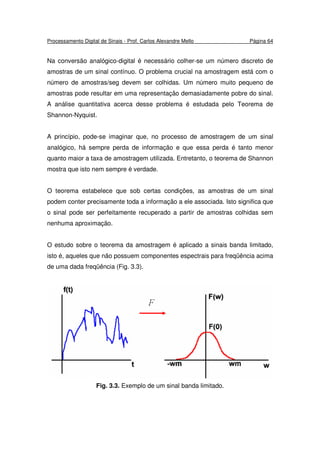
como na Fig. 3.1.
Fig. 3.1. Exemplo: (esquerda) sinal original e (direita) amostragem desse sinal.
A forma mais comum de obter uma representação discreta no tempo de um sinal
contínuo no tempo é através de uma amostragem periódica, quando a
seqüência de amostras x[n] é obtida de um sinal contínuo no tempo xc(t) de
acordo com a relação:
x[n] = xc(nT), -∞ < n < ∞ (Eq. 3.1)
Na Eq. 3.1, T é chamado de período de amostragem e sua inversa, fs = 1/T, é a
freqüência de amostragem, medida em amostras por segundo.
Referimo-nos a um sistema que implementa a operação da Eq. 3.1 como um
conversor ideal contínuo-para-discreto (C/D) no tempo. Na prática, a operação](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-60-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 61
de amostragem é implementada por um conversor analógico-para-digital (A/D).
Tais sistemas podem ser vistos como aproximações de conversores C/D ideais.
Na implementação ou escolha de um conversor A/D deve-se considerar a
quantização da saída, linearidade, a necessidade de circuitos sample-and-hold e
limitações na taxa de amostragem.
Em geral, a amostragem é um processo não-inversível. Ou seja, dada uma
seqüência x[n], não é possível reconstruir o sinal original xc(t). Muitos sinais
diferentes podem gerar a mesma seqüência de amostras de saída.
É conveniente representarmos matematicamente o processo de amostragem,
dividindo-o em duas partes conforme a Fig. 3.2. O processo consiste de um trem
de impulsos seguido de uma conversão desse trem em uma seqüência. Na Fig.
3.2, a diferença fundamental entre xs(t) e x[n] é que xs(t) é um sinal contínuo com
valores zero exceto nos inteiros múltiplos de T. x[n], por outro lado, não possui
informação explícita sobre a taxa de amostragem e é um sinal onde as regiões
que não representam valores inteiros não têm valor definido.
São muitas as razões para o aumento no uso de sistemas digitais:
1. Muitas informações (ou dados) estão nessa forma, e.g. entrada/saída de
computadores, sinais de controle digital, etc.
2. A disponibilidade de componentes pequenos, confiáveis e de baixo custo,
principalmente, com o aumento da escala de integração dos circuitos
integrados.
3. Relativa simplicidade no projeto de circuitos e facilidade de
implementação usando circuitos integrados.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-61-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 62
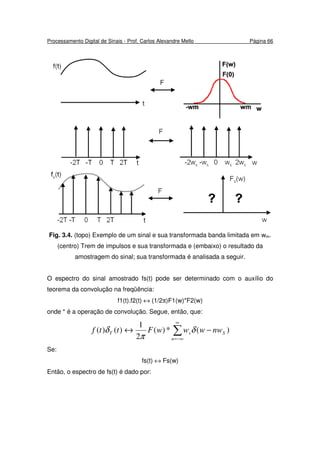
Fig. 3.2. Amostragem com um trem de impulsos periódicos seguida de uma
conversão para uma seqüência discreta no tempo. a) Visão geral do sistema; b)
xc(t) (sinal original no tempo contínuo) e xs(t); c) a seqüência x[n] de saída.
4. Ampla utilização de computadores digitais no processamento de todo tipo
de dados e sinais.
5. Armazenamento de sinais realizado de modo simples e econômico
(simplicidade das memórias digitais)
6. Crescente uso e disponibilidade de técnicas de processamento digital de
sinais (DSP).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-62-320.jpg)



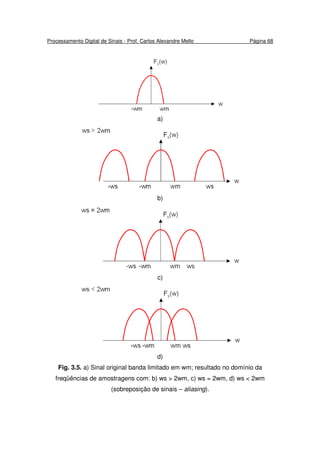
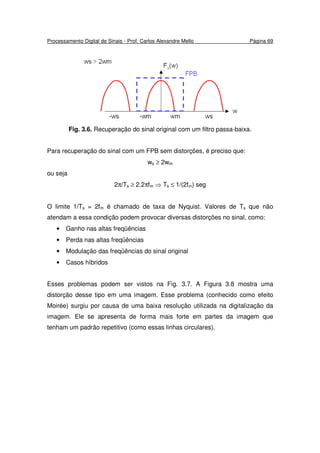
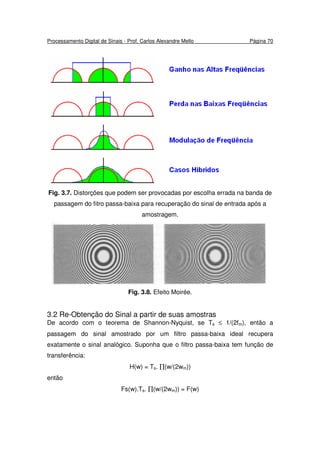
()[()( δ
π
Lembrando da propriedade da amostragem da função impulso, segue-se
∑
∞
−∞=
−=
n
smssm nTtwSanTfTftf ))(()(.2)(
No caso particular em que Ts = 1/(2fm), tem-se
∑
∞
−∞=
−=
n
m
m
ntwSa
f
n
ftf )()
2
()( π
Como o sinal é recomposto através das amostras, observa-se que f(t)
corresponde à superposição de várias funções sample deslocadas, centradas
em 0, ±T, ±2T, .... (Fig. 3.9).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-71-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 73
4. Filtros Digitais
Um sistema discreto no tempo é definido matematicamente como uma
transformação que mapeia uma seqüência de entrada x[n] em uma seqüência
de saída y[n]. Isso pode ser denotado por:
y[n]=T{x[n]}
como representado na Fig. 4.1.
Fig. 4.1. Representação de um sistema discreto no tempo
Uma classe importante de sistemas consiste naqueles que são lineares e
invariantes no tempo. Os sistemas lineares são aqueles que obedecem ao
princípio da superposição. Se a propriedade da linearidade é combinada com a
representação de uma seqüência geral como uma combinação de impulsos,
então um sistema linear pode ser completamente caracterizado pela sua
resposta ao impulso. Seja hk[n] a resposta do sistema a δ[n – k]. Assim, como:
∑
∞
−∞=
−=
k
knkxnx ][][][ δ
então
}][][{][ ∑
∞
−∞=
−=
k
knkxTny δ
Pelo princípio da superposição, podemos escrever:
∑∑
∞
−∞=
∞
−∞=
=−=
k
k
k
nhkxknTkxny ][][}][{][][ δ
De acordo com essa equação, a resposta do sistema a qualquer entrada pode
ser expressa em termos da resposta a δ[n – k] (o impulso).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-73-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 74
A propriedade da invariância no tempo implica que, se h[n] é a resposta a δ[n],
então a resposta a δ[n - k] é h[n – k]. Com isso, podemos dizer que:
∑
∞
−∞=
−=
k
knhkxny ][][][ (Eq. 4.1)
Como conseqüência, um sistema linear invariante no tempo é completamente
descrito por sua resposta ao impulso. Essa equação é conhecida como soma de
convolução (convolution sum) que pode ser representada pela notação:
y[n] = x[n]*h[n] (Eq. 4.2)
Apesar da semelhança na notação, deve-se salientar que a soma de convolução
para sinais discretos não é uma aproximação da integral de convolução.
Para qualquer que seja a entrada x[n] de um sistema:
x[n]* δ[n] = x[n]
Assim, em geral, se um sistema linear invariante no tempo tem uma resposta ao
impulso h[n], então seus sistema inverso, se existir, tem resposta ao impulso
hi[n] definida pela relação:
h[n]*hi[n] = hi[n]*h[n] = δ[n]
Uma classe importante de sistemas lineares invariantes no tempo consiste
daqueles para os quais x[n] e y[n] se relacionam através de uma equação de
diferenças de coeficientes constantes lineares de n-ésima ordem da forma:
∑ ∑= =
−=−
N
k
M
k
kk knxbknya
0 0
][][ (Eq. 4.3)
Um exemplo de um tal sistema é um acumulador definido pela seqüência cujo
diagrama de blocos pode ser visto na figura abaixo:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-74-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 75
Esse sistema é representado pela equação de diferenças:
y[n] = y[n – 1] + x[n]
ou
y[n] - y[n – 1] = x[n]
Pela Eq. 4.3, temos: N = 1, a0 = 1, a1 = -1, M = 0 e b0 = 1.
4.1 Filtros Digitais
Em geral, estamos interessados em manipular o sinal. Por exemplo, podemos
querer retirar algum ruído de um sinal, como no caso de um sinal de voz, onde o
ruído deve ser diferenciado da voz propriamente dita. Para isso, filtros são
utilizados. Filtros estão envolvidos em diversas partes de um sistema de
processamento digital de sinal. Eles podem ser implementados tanto em
hardware quanto em software e atuam em sinais digitais de diversas naturezas,
como sons, voz, imagem ou vídeo. Em cada caso, os filtros assumem
particularidades diferentes. Vamos entender um pouco como se dá o processo
em sinais e, em seguida, particularizar para o caso de imagens digitais.
Filtros digitais são formados por poucos componentes. Basicamente são apenas
multiplicadores, somadores e elementos de retardo (delay). Desses,
multiplicadores e somadores implementam essas operações aritméticas em
seqüências discretas. Retardos são unidades que processam elementos
anteriores de uma seqüência (Fig. 4.2).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-75-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 76
Fig. 4.2. Retardo (delay) aplicado a uma seqüência x[n].
A representação mostrada na Fig. 4.2 em diagrama de blocos é comum para
filtros. Os elementos básicos de um filtro também são representados dessa
maneira. Nesse caso, o elemento de delay é representado como z-1
, devido à
Transformada Z. As representações em diagrama de blocos podem ser vistas na
Fig. 4.3.
Fig. 4.3. Diagrama de blocos de: a) Somador de duas seqüências, b)
multiplicador de duas seqüências, c) multiplicador de uma seqüência por uma
constante e d) retardo.
Exemplos:
1) Podemos ver na Fig. 4.4 a representação em diagrama de blocos da equação
de diferença definida por:
y[n] = a1.y[n – 1] + a2.y[n – 2] + b.x[n]](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-76-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 77
cuja transformada Z (ou função de sistema) é dada por:
2
2
1
11
)( −−
−−
=
zaza
b
zH
Fig. 4.4. Diagrama de blocos para uma equação de diferenças.
2) Uma equação de diferenças pode ser generalizada da forma:
∑ ∑= =
−=−−
N
k
M
k
kk knxbknyany
1 0
][][][
com função de sistema correspondente:
)(
)(
1
)(
1
0
zX
zY
za
zb
zH N
k
k
k
M
k
k
k
=
−
=
∑
∑
=
−
=
−
A função de sistema ou função de transferência corresponde à relação entre a
saída e a entrada do sistema.
Podemos re-escrever a equação de diferenças na forma de uma relação de
recorrência:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-77-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 78
∑ ∑= =
−+−=
N
k
M
k
kk knxbknyany
1 0
][][][
que pode ser representada em diagrama de blocos como na Fig. 4.5.
Fig. 4.5. Representação em diagrama de blocos de uma equação de diferenças
geral.
Nessa figura, temos:
∑=
−=
M
k
k knxbnv
0
][][
∑=
−+=
N
k
k knyanvny
1
][][][
Como apresentado na Fig. 4.5, referimos a essa forma de diagrama de blocos
como a Forma Direta I. Uma implementação com uma menor quantidade de
retardos também pode ser utilizada e é chamada de Forma Direta II (Fig. 4.6,
considerando, sem perda de generalizada, M = N).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-78-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 80
Fig. 4.7. Exemplo de um filtro FIR.
Suponha na Fig. 4.7 que o sistema tem uma entrada x[n] = [1, 0]. Sendo um
sistema causal, a entrada para n < 0 é igual a zero. Assim, para n = 0, temos:
E, para n = 1:
Logo, a saída seria y[n]=[0.5, 0.5]. A equação para cada termo é:
y[0] = 0.5.x[0] + 0.5.x[-1]
y[1] = 0.5.x[1] + 0.5.x[0]](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-80-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 81
Ou, de forma geral:
y[n] = 0.5.x[n] + 0.5.x[n - 1]
Os filtros FIR são expressos como:
∑=
−=
M
k
k knxbny
0
][][
com função de transferência:
∑=
−
=
M
k
k
k zbzH
0
)(
A resposta ao impulso h[n] é dada por:
−≤≤
=
senão
Mnb
nh n
0
10
][
e a representação em equação de diferenças é:
y[n] = b0x[n] + b1x[n – 1] + ... + bN-1x[n – M + 1]
Um filtro FIR pode ser representado em forma direta como:
Por simplicidade, pode-se representar um filtro FIR apenas com seus
coeficientes. Por exemplo, seja um filtro FIR com coeficientes [1, -1], ele pode
ser representado como:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-81-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 82
Dados os coeficientes, pode-se calcular de forma simples a saída do sistema
para uma dada entrada. Considere uma entrada x[n]=[1, 2, 3, 4, 5] em um filtro
com coeficientes [6, 7, 8]. A saída é dada por:
Há três importantes propriedades de um sistema:
• Causalidade
• Linearidade
• Invariância no tempo
Um sistema é dito causal quando ele não precisa de informações futuras para
calcular a saída atual. Um sistema é linear se obedece ao princípio da
superposição. Ou seja:
T{a.x1[n] + b.x2[n]} = a.T{x1[n]} + b.T{x2[n]}
Por último, um sistema é dito invariante no tempo se a saída do sistema reflete
qualquer deslocamento que a entrada. Ou seja, se y[n] = T{x[n]}, então x[n – m]
gera uma saída y[n – m].
Filtros FIR podem implementar diversas diferentes funções apenas com
mudanças nos seus coeficientes. A função de um filtro depende de seu
comportamento no domínio da freqüência. Um filtro pode ser passa-baixa,
passa-alta, passa-faixa, rejeita-faixa ou notch. Um filtro notch é um filtro que tem
fendas profundas ou, idealmente, zeros perfeitos na sua resposta em frequência.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-82-320.jpg)
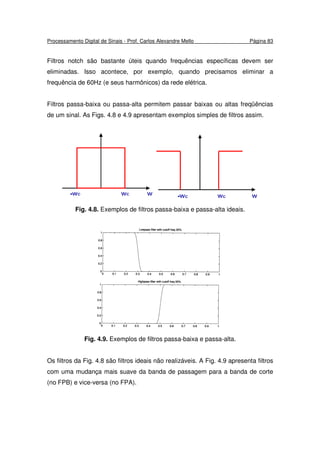
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 84
Na prática, tais filtros têm características um pouco diferentes. Podemos
observar ondulações e uma banda de transição mais suave. Essas
características podem ser vistas na Fig. 4.10 a qual apresenta o espectro de
diferentes filtros (ou seja, suas transformadas de Fourier). É através do espectro
que podemos analisar o comportamento do filtro.
Fig. 4.10. Padrões de ondulação na banda de passagem ou na banda de parada
e um banda de transição suave.
Por exemplo, um filtro apenas com coeficientes [0,5 0,5] comporta-se como um
FPB. Seu comportamento foi avaliado anteriormente, tendo sua saída definida
por:
y[n] = 0.5.x[n] + 0.5.x[n - 1]](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-84-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 85
que é o mesmo que y[n] = (x[n] + x[n – 1])/2. Por isso, filtros passa-baixa são
chamados, às vezes, de filtro da média.
Um filtro com coeficientes [0,5 -0,5] corresponde a um filtro passa-alta, chamado
de filtro de diferenciação. O seguinte código no MatLab apresenta a
transformada de Fourier para uma seqüência de coeficientes. A Fig 4.11
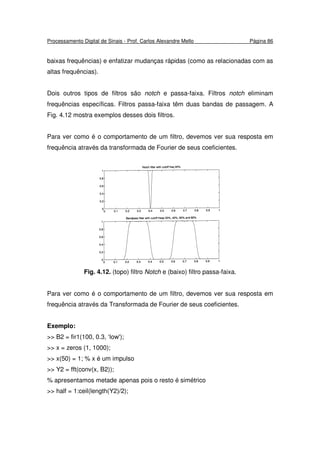
apresenta os resultados para os coeficientes [0,5 0,5] e [0,5 -0,5].
x = [0.5, -0.5];
f = fft(x,8192);
Freq = -5:10/8192:5-1/8192;
plot(Freq, abs(fftshift(f)));
Fig. 4.11. (esquerda) Seqüência [0,5 0,5] e sua transformada de Fourier (um
FPB) e (direita) a seqüência [0,5 -0,5] e sua transformada (um notch FPA).
Vamos analisar o FPA:
y[n] = (x[n] - x[n – 1])/2
Pequenas diferenças entre as amostras resultam em valores pequenos; grandes
diferenças resultam em valores grandes. Assim, a resposta em frequência desse
filtro deve atenuar mudanças suaves no sinal (como as relacionadas com as](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-85-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 88
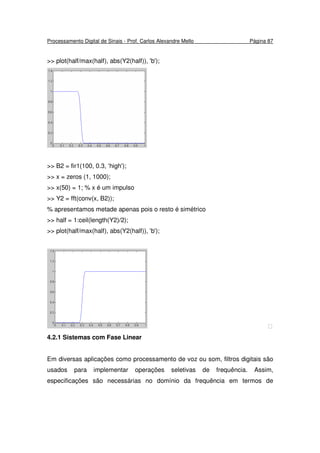
magnitude desejada e resposta em fase do filtro. Em geral, uma resposta em
fase linear na banda de passagem é desejada (Fig. 4.13).
Fig. 4.13. Exemplos de fases lineares e não-lineares.
Considere um sistema LTI cuja reposta em frequência sobre um período é:
Hid(ejω
)=e-jωα
, |ω| < π
onde α é um número real, não necessariamente um inteiro. Esse sistema tem
magnitude constante:
|Hid(ejω
)| = 1,
fase linear
∠Hid(ejω
) = -ωα
e atraso de grupo constante
grd[Hid(ejω
)] = α
A transformada inversa de Fourier de Hid(ejω
) é dada por:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-88-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 89
∫∫ −
−−
−
−
==
π
π
αω
π
π
ωωα
ω
π
ω
π
dedeenh njnjj
id
)(
2
1
2
1
][
=
−
=
−
=
−
−−
−
−− π
π
αωπ
π
αω
απαπ
)()(
)(
1
2
1
)(
1
2
1 njjnj
e
nj
e
nj
][
)(
1
2
1 )()( njnj
ee
nj
−−−
−
−
= απαπ
απ
Sabendo que 2/)( αα
α jj
eesen −
−= , temos:
)]([
)(
1
][
)(
1
2
1 )()(
απ
απαπ
απαπ
−
−
=−
−
−−−
nsen
n
ee
nj
njnj
)(
)]([
][
απ
απ
−
−
=
n
nsen
nhid , -∞< n < ∞ (Eq. 1)
Assim
)(
)]([
*][][*][][
απ
απ
−
−
==
n
nsen
nxnhnxny id
∑
∞
−∞= −−
−−
=
k kn
knsen
kxny
)(
)]([
][][
απ
απ
Se α = nd, nd inteiro, pela propriedade do deslocamento do tempo da
transformada de Fourier e lembrando que ℑ{δ[n]} = 1 :
Hid(ejω
) = e-jωnd
↔ hid[n] = δ[n – nd]
Logo:
][*][][ dnnnxny −= δ
Ou seja, a mesma seqüência de entrada apenas deslocada de nd amostras.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-89-320.jpg)
2(
)]2([
]2[
dd
ddc
dLP
nnn
nnnsen
nnh
π
ω
][
)(
)]([
]2[ nh
nn
nnsen
nnh LP
d
dc
dLP =
−
−
=−⇒
π
ω
Nesse caso, temos um sistema de fase zero (zero phase system). Se α = -nd:
][][|)(|)()(
^^^
nhnheHeeHeH LPLP
j
LP
njj
LP
j
LP
d
−=⇒== ωωωω
Assim, se 2α é um inteiro (o que implica que α é um inteiro ou um inteiro mais
0.5), a resposta ao impulso correspondente tem simetria sobre α, i.e.:
h[2α - n] = h[n]
Isso é condição suficiente (mas não necessária) para termos um sistema de fase
linear.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-90-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 91
Fase Linear Generalizada
Um sistema é dito de fase linear generalizada se sua resposta em freqüência
pode ser expressa na forma:
H(ejω
) = A(ejω
)e-jαω+jβ
(Eq. 2)
onde α e β são constantes e A(ejω
) é uma função real ω. O sistema que
consideramos antes tinha β = 0. Um sistema como o da Eq. 2 é dito de fase
linear generalizada dado que a fase é uma função linear de -ωα. Tal sistema
também se caracteriza por um atraso de grupo constante:
grd[H(ejω
)] = α
De forma geral, a fase linear tem forma:
∠[H(ejω)] = β - ωα, 0 < ω < π
onde α e β são constantes reais. Lembramos que, como vimos antes, a resposta
ao impulso de sistemas de fase linear tem simetria sobre α, se 2α é um inteiro.
Temos que, se:
)]())[cos(()( ωαβωαβωω
−+−= jseneAeH jj
ou
)()()cos()()( ωαβωαβ ωωω
−+−= senejAeAeH jjj
Equivalentemente, por definição:
∑∑∑
∞
−∞=
∞
−∞=
∞
−∞=
−
−==
nnn
njj
nsennhjnnhenheH ωωωω
][cos][][)(
com h[n] real.
Assim:
)()()cos()()( ωαβωαβ ωωω
−+−= senejAeAeH jjj
e](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-91-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 92
∑∑∑
∞
−∞=
∞
−∞=
∞
−∞=
−
−==
nnn
njj
nsennhjnnhenheH ωωωω
][cos][][)(
Logo, podemos considerar:
∑
∞
−∞=
=−
n
j
nnheA ωωαβω
cos][)cos()(
e
∑
∞
−∞=
−=−
n
j
nsennhseneA ωωαβω
][)()(
Com isso:
∑
∑
∞
−∞=
∞
−∞=
−
=
−
−
=−
n
n
nnh
nsennh
sen
tg
ω
ω
ωαβ
ωαβ
ωαβ
cos][
][
)cos(
)(
)(
Fazendo uma multiplicação cruzada dos dois lados da igualdade acima, temos:
∑∑
∞
−∞=
∞
−∞=
−−=−
nn
nsennhnnhsen ωωαβωωαβ ][)cos(cos][).(
0][)cos(cos][).( =−+−⇒ ∑∑
∞
−∞=
∞
−∞= nn
nsennhnnhsen ωωαβωωαβ
0)cos(][.cos)(][ =−+−⇒ ∑∑
∞
−∞=
∞
−∞= nn
nsennhnsennh ωωαβωωαβ
0])cos(.cos)(][[ =−+−⇒ ∑
∞
−∞=n
nsennsennh ωωαβωωαβ
0)(][ =+−⇒ ∑
∞
−∞=n
nsennh ωωαβ](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-92-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 93
0])([][ =+−⇒ ∑
∞
−∞=n
nsennh βαω (Eq. 3)
ou
0})](cos[.cos)]([]{[ =−+−∑
∞
−∞=n
sennnsennh βαωβαω (Eq. 4)
para todo valor de ω. Assim, se β = 0 ou π, a Eq. 4 torna-se:
0)]([][ =−∑
∞
−∞=n
nsennh αω (Eq. 5)
Se β = π/2 ou 3π/2, a Eq. 4 torna-se:
0)](cos[][ =−∑
∞
−∞=n
nnh αω (Eq. 6)
Na Eq. 5, se h[n] = h[2α - n], com 2α inteiro:
0)]2([]2[0)]([][ =−−−⇒=− ∑∑
∞
−∞=
∞
−∞= nn
nsennhnsennh ααωααω
0)]([]2[ =−−⇒ ∑
∞
−∞=n
nsennh αωα (Eq. 7)
A Eq. 7 tem as mesmas soluções da Eq. 5, se 2α é um inteiro (ou seja, α é um
inteiro ou um inteiro mais 0.5). Assim, se β = 0 ou π, 2α = M inteiro, podemos ter
h[2α - n] = h[n]. De forma similar, na Eq. 6, se β = π/2 ou 3π/2, 2α = M inteiro,
podermos ter h[2α - n] = -h[n].
Com isso, temos dois conjuntos de condições para garantir um sistema de fase
linear generalizada:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-93-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 94
i)
β = 0 ou π
2α = M inteiro
h[2α - n] = h[n]
ii)
β = π/2 ou 3π/2
2α = M inteiro
h[2α - n] = -h[n]
Sistemas Causais de Fase Linear Generalizada
Se o sistema for causal, a Eq.3 torna-se:
0])([][
0
=+−∑
∞
=n
nsennh βαω
para todo valor de ω.
Causalidade implica h[n] = 0, para n < 0 e n > M (para um sistema FIR, já que a
resposta ao impulso é finita), i.e., sistemas FIR causais têm fase linear
generalizada se eles têm resposta ao impulso de comprimento (M + 1) e
satisfaz:
h[2α - n] = h[n]
ou
h[2α - n] = -h[n]
No primeiro caso, temos, para β = 0 ou π:
][
)(
)(
)(
)(
)2(
)2(
]2[ nh
n
nsen
n
nsen
n
nsen
nh =
−
−
−=
−
−
=
−−
−−
=−
απ
απ
απ
απ
ααπ
ααπ
α
O segundo caso acontece para β = π/2 ou 3π/2.
Especificamente, se](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-94-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 95
h[n] = h[M – n], 0 ≤ n ≤ M,
e 0, caso contrário
então pode ser mostrado que
H(ejω
) = AP(ejω
)e-jωM/2
onde AP(ejω
) é uma função real, par e periódica em w. De forma similar, se
h[n] = -h[M – n], 0 ≤ n ≤ M,
e 0, caso contrário
segue que:
H(ejω
) = jAI(ejω
)e-jωM/2
= AI(ejω
)e-jωM/2 + jπ/2
onde AI(ejω
) é uma função real, ímpar e periódica em ω. Em ambos os casos, o
comprimento da resposta ao impulso é (M + 1) amostras.
Dependendo da sua resposta ao impulso, os filtros FIR podem ser divididos em
quatro classes:
1. Sistemas FIR com fase linear do Tipo I
Um sistema do tipo I tem resposta ao impulso simétrica
h[n] = h[M – n], 0 ≤ n ≤ M
com M um inteiro par (observe que isso gera um número ímpar de amostras). O
atraso M/2 é um inteiro. A resposta em frequência é:
∑=
−
=
M
n
njj
enheH
0
][)( ωω
Considerando a condição de similaridade, essa resposta em frequência pode ser
expressa como:
∑=
−
=
2/
0
2/
)cos(][)(
M
k
Mjj
kkaeeH ωωω
onde a[0] = h[M/2],
a[k] = 2h[(M/2) – k], k = 1, 2, 3, ..., M/2](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-95-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 96
Assim, H(ejw
) tem a forma de AP(ejw
)e-jwM/2
.
2. Sistemas FIR com fase linear do Tipo II
Um sistema do tipo II tem uma resposta ao impulso simétrica como
h[n] = h[M – n], 0 ≤ n ≤ M
mas com M um inteiro ímpar. Nesse caso, H(ejw
) pode ser expresso como:
}]
2
1
(cos[][{)(
2/)1(
1
2/
∑
+
=
−
−=
M
k
Mjj
kkbeeH ωωω
onde
b[k] = 2.h[(M + 1)/2 - k], k = 1, 2, ..., (M + 1)/2
Novamente H(ejw
) tem a forma de AP(ejw
)e-jwM/2
.
3. Sistemas FIR com fase linear do Tipo III
Se o sistema tem uma resposta ao impulso assimétrica:
h[n] = -h[M - n], 0 ≤ n ≤ M
com M um inteiro par, então H(ejw
) tem a forma:
∑=
−
=
2/
0
2/
)sin(][)(
M
k
Mjj
kkcjeeH ωωω
onde
c[k] = 2h[(M/2) - k], k = 1, 2, ..., M/2
Nesse caso, H(ejw
) tem a forma:
H(ejw
) = AI(ejw
)e-jwM/2 + jπ/2
4. Sistemas FIR com fase linear do Tipo IV
Se o sistema tem uma resposta ao impulso assimétrica:
h[n] = -h[M - n], 0 ≤ n ≤ M
com M um inteiro ímpar, então H(ejw
) tem a forma:
}]
2
1
(sin[][{)(
2/)1(
1
2/
∑
+
=
−
−=
M
k
Mjj
kkdjeeH ωωω](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-96-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 97
onde
d[k] = 2h[(M+1)/2 - k], k = 1, 2, ..., (M + 1)/2
e H(ejw
) tem a forma:
H(ejw
) = AI(ejw
)e-jwM/2 + jπ/2
Exemplos:
a) Tipo I, resposta simétrica, M par
h[n] = 1, 0 ≤ n ≤ 4, e 0, caso contrário
h[n] = h[M – n]
A resposta em frequência é:
)2/sin(
)2/5sin(
1
1
)( 2
54
0 w
w
e
e
e
eeH jw
jw
jw
n
jwnjw −
−
−
=
−
=
−
−
== ∑
Magnitude e fase:
b) Tipo II, resposta simétrica, M ímpar
h[n] = 1, 0 ≤ n ≤ 5, e 0, caso contrário](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-97-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 98
h[n] = h[M – n]
A resposta em frequência é:
)2/sin(
)3sin(
)( )2/5(
w
w
eeH jwjw −
=
Magnitude e fase:
c) Tipo III, resposta assimétrica, M par
Se h[n] = δ[n] - δ[n – 2]
Então H(ejw
) = 1 – e-2jw
= j[2.sin(w/2)]e-jw
Magnitude e fase:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-98-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 99
d) Tipo IV, resposta assimétrica, M ímpar
Se h[n] = δ[n] - δ[n – 1]
Então H(ejw
) = 1 – e-jw
= j[2.sin(w/2)]e-jw/2
Magnitude e fase:
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-99-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 100
Exemplo: O seguinte código implementa no MatLab um filtro FIR tipo I:
h = [3 4 5 6 5 4 3]/30; % Veja que vai de zero a seis
M = length(h);
N = (M-1)/2;
L = 512;
H = fft([h zeros(1,L-M)]);
k = 0:L-1;
W = exp(j*2*pi/L);
A = H.* W.^(N*k);
A = real(A);
figure(1)
w = [0:L-1]*2*pi/(L-1);
subplot(2,1,1)
plot(w/pi,abs(H))
ylabel('|H(omega)| = |A(omega)|')
xlabel('omega/pi')
subplot(2,1,2)
plot(w/pi,A)
ylabel('A(omega)')
xlabel('omega/pi')
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-100-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 101
Exemplo: O seguinte código implementa no MatLab um filtro FIR tipo II:
h = [3 5 6 7 7 6 5 3]/42;
M = length(h);
N = (M-1)/2;
L = 512;
H = fft([h zeros(1,L-M)]);
k = 0:L-1;
W = exp(j*2*pi/L);
A = H.* W.^(N*k);
A = real(A);
figure(2)
w = [0:L-1]*2*pi/(L-1);
subplot(2,1,1)
plot(w/pi,abs(H))
ylabel('|H(omega)| = |A(omega)|')
xlabel('omega/pi')
subplot(2,1,2)
plot(w/pi,A)
ylabel('A(omega)')
xlabel('omega/pi')
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-101-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 102
4.3 Filtros IIR
Os filtros FIR usam apenas cálculos feed forward. Se feedback é permitido, a
resposta de um filtro ao impulso não será necessariamente finita. Assim, filtros
com feedback são chamados de filtros com resposta ao Impulso Infinita (IIR –
Infinite Impulse Response). Por exemplo, o filtro abaixo:
cuja equação que descreve sua saída é dada por:
y[n] = 0,6.x[n] + 0,2.x[n-1] + 0,4.y[n – 1]
Se um impulso passa por esse filtro teremos como resposta as seguintes saídas,
considerando o filtro causal:
Entrada Saída
0 0
1 0,6
0 0,44
0 0,176
.... ....
Ou seja, mesmo quando a entrada se anula, o filtro continua apresentando uma
saída. Essa saída diminui, mas não torna-se zero. Claro que, na prática, a
resposta chega a zero em algum momento. Considere então o filtro a seguir:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-102-320.jpg)
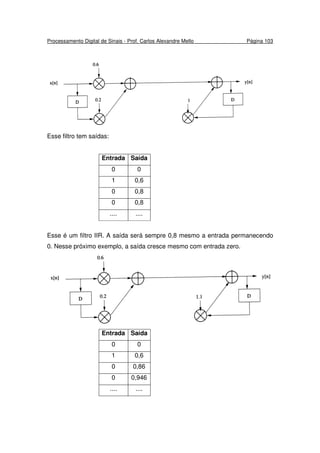
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 104
De uma maneira geral, os filtros IIR são expressos como:
∑ ∑= =
−=−−
N
k
M
k
kk knxbknyany
1 0
][][][
com a seguinte função de sistema:
∑
∑
=
−
=
−
−
= N
k
k
k
M
k
k
k
za
zb
zH
1
0
1
)(
Suas formas Direta I e Direta II são mostradas nas Figs. 4.14 e 4.15.
Fig. 4.14. Forma Direta I de um filtro IIR](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-104-320.jpg)






![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 111
filtros FIR. A segunda forma é chamada de especificações relativas que provê os
requisitos em decibéis (dB) e é dada por:
escala dB = 0
|)(|
|)(|
log20
max
10 ≥− ω
ω
j
j
eH
eH
Essa é a forma mais comum na prática e é usada tanto para filtros FIR quanto
IIR. Vamos considerar o projeto de um filtro passa-baixa como exemplo.
Uma especificação absoluta de um filtro passa-baixa é mostrada na Fig. 5.1 na
qual:
• A banda [0, wp] é chamada de banda de passagem, e δ1 é a tolerância a
qual são permitidas ondulações (ripples) na resposta ideal da banda de
passagem;
• A banda [ws, π] é chamada de banda de corte, e δ2 é a tolerância a qual
são permitidas ondulações;
• A banda [ws, wp] é chamada de banda de transição, e não há qualquer
restrição na resposta em magnitude nessa banda.
Fig. 5.1. Especificação absoluta de um filtro passa-baixa real: banda de
passagem, banda de transição e banda de corte.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-111-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 112
A especificação relativa de um filtro passa-baixa pode ser vista na Fig. 5.2 na
qual:
• Rp é a ondulação na banda de passagem em dB, e
• As é a atenuação na banda de corte em dB.
Fig. 5.2. Especificação relativa de um filtro passa-baixa real.
Os parâmetros das duas especificações são relacionados. Como |H(ejw
)|max na
especificação absoluta é igual a (1 + δ1), temos:
0
1
1
log20
1
1
10 >
+
−
−=
δ
δ
PR e
0
1
log20
1
2
10 >
+
−=
δ
δ
SA
Exemplo:
As especificações de um FPB definem as ondulações da banda de passagem
em 0,25 dB e a atenuação na banda de corte em 50 dB. Determine δ1 e δ2.
RP = 0,25 = -20 log10 [(1 - δ1)/(1 + δ1)] ⇒ δ1 = 0,0144
AS = 50 = -20 log10 [δ2/(1 + δ1)] ⇒ δ2 = 0,0032
Especificações semelhantes podem ser dadas para outros tipos de filtros
seletores de frequência (como passa-alta ou passa-faixa).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-112-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 113
Analisaremos o problema de especificar um filtro passa-baixa e, facilmente,
esses conceitos podem ser repassados para outros tipos de filtros.
Nosso problema é projetar um filtro passa-baixa (i.e., obter sua função de
transferência H(z) ou sua equação de diferenças) que tem uma banda de
passagem [0, wp] com tolerância δ1 (ou RP in dB) e uma banda de corte [wS, π]
com tolerância δ2 (ou AS in dB).
A seguir, vamos projetar filtros digitais FIR. Esses filtros têm diversas vantagens
de projeto e implementação:
• A resposta em fase pode ser exatamente linear;
• São relativamente simples de projetar já que eles não têm problemas de
estabilidade;
• São eficientes para implementar;
• A Transformada Discreta de Fourier pode ser usada em sua
implementação.
5.1 Projeto de Filtros FIR
Tanto a aproximação quanto a implementação podem ser realizadas de diversas
maneiras diferentes, com o resultado de que não existe uma solução única para
o problema de projeto de filtros com um conjunto prescrito de especificações.
Todavia, podemos mencionar três diferentes abordagens para o projeto de filtros
analógicos e digitais:
• Abordagem analógica, a qual se aplica à classe de filtros analógicos.
• Abordagem de analógico para digital, em que a motivação é projetar um
filtro digital lançando mão de um projeto de filtro analógico.
• Abordagem digital direta a qual se aplica à classe de filtros digitais.
Para o projeto de filtros FIR, as técnicas são divididas nas seguintes categorias:
• Projeto usando janelas](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-113-320.jpg)
(
)]([
.1
2
1
][
απ
αω
ω
π
ω
ω
ωαω
−
−
== ∫−
−
n
nsen
deenh cnjj
d
C
C
Para obter um filtro FIR a partir de hd[n], precisamos truncar hd[n] em ambos os
lados. Para obter um filtro FIR causal de fase linear h[n] de comprimento M,
devemos ter:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-114-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 115
−≤≤
=
senão
Mnnh
nh d
,0
10],[
][
e
α = (M – 1)/2.
Essa operação é chamada de janelamento. Em geral, h[n] pode ser pensado
como sendo formado pelo produto de hd[n] e uma janela w[n] tal que:
h[n] = hd[n].w[n]
onde w[n] é alguma função simétrica com respeito a α no intervalo 0 ≤ n ≤ M – 1
e 0 fora desse intervalo.
Dependendo de como obtivermos w[n] acima, temos diferentes projetos de
filtros. Por exemplo:
−≤≤
=
senão
Mn
nw
,0
10,1
][
é uma janela retangular.
No domínio da frequência, a resposta H(ejw
) do filtro FIR causal é dada pela
convolução de Hd(ejw
) e a resposta da janela W(ejw
):
∫−
−
==
π
π
λλ
λ
π
deHeWeWeHeH wj
d
jjwjw
d
jw
)()(
2
1
)(*)()( )(
Podemos ver essa convolução na Fig. 5.3 para uma janela comum.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-115-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 116
Fig. 5.3. Operação de janelamento no domínio da frequência.
Observações:
1. Como a janela w[n] tem comprimento finito igual a M, sua resposta em
frequência tem uma região de pico central (lóbulo principal) cuja largura é
proporcional a 1/M e tem lóbulos laterais com pesos menores.
2. A convolução gera uma versão da resposta ideal Hd(ejw
), mas com algumas
distorções (ondulações).
3. A largura da banda de transição é proporcional a 1/M.
4. Os lóbulos laterais produzem ondulações que têm forma similar tanto na
banda de passagem quanto na de corte.
Projeto usando janelas: Para uma dada especificação de filtro, escolha um
filtro de comprimento M e uma função janela w[n] para a mais estreita largura do
lóbulo principal e a menor atenuação nos lóbulos laterais possível.
Da observação 4 acima, podemos notar que a tolerância δ1 da banda de
passagem e a tolerância δ2 da banda de corte não podem ser especificadas de
forma independente. Geralmente, toma-se δ1 = δ2.
Vamos descrever alguns tipos comuns de funções de janelamento.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-116-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 117
1) Janela Retangular
Essa é a janela mais simples, mas que provê o pior desempenho em termos de
atenuação da banda de corte. Ela é definida como:
≤≤
=
senão
Mn
nw
,0
0,1
][
sendo sua resposta em frequência:
)2/(
]2/)1([
1
1
)( 2/
0
)1(
wsen
Mwsen
e
e
e
eeW jwM
M
n
jw
Mjw
jwnjw +
=
−
−
== −
=
−
+−
−
∑
A magnitude da função sen[w(M + 1)/2]/sen(w/2) é mostrada na Fig. 5.4 para o
caso de M = 7. Note que W(ejw
) tem fase linear generalizada. À medida que M
aumenta, a largura do lóbulo principal diminui.
Fig. 5.4. Magnitude da transformada de Fourier de uma janela retangular (M =
7).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-117-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 118
Pode ser provado que a largura do lóbulo central é ∆wm = 4π/(M + 1) para uma
janela retangular. O primeiro zero de W(ejw
) ocorre quando:
sen (w(M + 1)/2) = 0 ⇒ w(M + 1)/2 = π ⇒ 2π/(M + 1)
Assim, a largura do lóbulo central é o dobro desse valor (já que envolve os
valores negativos e positivos):
2w = 4π/(M + 1)
Observa-se também que a magnitude do primeiro lóbulo lateral é
aproximadamente em w = 3π/(M + 1) e é dada por:
ππ
π
3
)1(2
)1(2
3
)2/3(
)2/(
)]2/)1([( +
≅
+
=
+ M
M
sen
sen
wsen
Mwsen
À medida que M cresce, a largura de cada lóbulo lateral diminui, mas a área
sobre cada um permanece constante. Assim, as amplitudes relativas dos picos
laterais vão permanecer constantes e a atenuação da banda de passagem
permanece em cerca de 21 dB. Isso significa que as ondulações vão sofrer um
pico perto das bordas das bandas. Isso é conhecido como fenômeno de Gibbs
(Fig. 5.5). Esse fenômeno ocorre por causa da transição brusca de 0 para 1 (e
de 1 para 0) da janela retangular.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-118-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 119
Fig. 5.5. Fenômeno de Gibbs: Pico das ondulações nas fronteiras entre as
bandas.
2) Janela Triangular ou de Bartlett
Bartlett sugeriu uma transição mais suave para evitar o fenômeno de Gibbs. Isso
seria conseguido através de uma janela triangular da forma:
≤<−
≤≤
=
senão
MnM
M
n
Mn
M
n
nw
,0
2/,
2
2
2/0,
2
][
Essa janela e sua resposta em frequência podem ser vistas na Fig. 5.6](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-119-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 120
Fig. 5.6. Janela triangular.
3) Janela de Hanning (homenagem a Julius von Hann, meteorologista
austríaco)
≤≤−
=
senão
MnMn
nw
,0
0),/2cos(5,05,0
][
π
Fig. 5.7. Janela de Hanning
4) Janela de Hamming (Richard Hamming, matemático americano)
≤≤−
=
senão
MnMn
nw
,0
0),/2cos(46,054,0
][
π
Tem uma quantidade menor de descontinuidades em relação à janela de
Hanning.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-120-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 121
Fig. 5.8. Janela de Hamming.
5) Janela de Blackman
≤≤+−
=
senão
MnMnMn
nw
,0
0),/4cos(08,0)/2cos(5,042,0
][
ππ
Também é similar às duas anteriores, mas tem um segundo harmônico o que faz
com que ela se aproxime de zero com mais suavidade.
Fig. 5.8. Janela de Blackman.
Tanto a janela de Bartlett, quanto Hamming, Hanning e Blackman têm lóbulos
laterais menores do que os da janela retangular. No entanto, para o mesmo
valor de M, a largura do lóbulo principal também é mais larga para essas janelas
se comparadas à janela retangular. Consequentemente, essas janelas
conseguem uma convolução no domínio da frequência mais suave e, como](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-121-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 122
resultado, a região de transição na resposta do filtro FIR é mais larga. Para
reduzir a largura da região de transição podemos aumentar o comprimento da
janela, o que resulta em filtros mais largos. A tabela a seguir resume algumas
características no domínio da frequência dessas janelas.
Tabela 5.1. Algumas características do domínio da frequência de algumas
funções de janelamento
Tipo de
janela
Largura de transição
aproximada do lóbulo
principal
Largura de
transição exata
Pico do
lóbulo
lateral (dB)
Retangular 4π/M 1,8π/M -21
Bartlett 8π/M 6,1π/M -25
Hanning 8π/M 6,2π/M -44
Hamming 8π/M 6,6π/M -53
Blackman 12π/M 11π/M -74
6) Janela de Kaiser (James F. Kaiser)
Esta é a melhor janela. Ela e considerada ótima porque provê um lóbulo
principal largo para a dada atenuação da banda de corte, o que implica a mais
brusca banda de transição. A função foi definida por Kaiser e é dada por:
≤≤
−−
=
senão
Mn
I
M
n
I
nw
,0
0,
][
2
11
][
0
2
0
β
β
I0(.) é a função de Bessel modificada de ordem zero:
∑
∞
=
+=
1
2
0
!
)2/(
1)(
n
n
n
x
xI](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-122-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 123
Fig. 5.8. Variadas formas da Janela de Kaiser.
Na expressão de w[n], existem dois parâmetros:
1. O comprimento M
2. O parâmetro β
Variando β e M, é possível ajustar a amplitude dos lóbulos laterais. Kaiser
encontrou duas fórmulas que permitem achar M e β de modo a atender às
especificações do filtro. Assim, dado que δ1 é fixo (especificado), a frequência de
corte wP da banda de passagem do filtro passa-baixa é a maior frequência tal
que:
|H(ejw
)| ≥ 1 - δ1
A frequência da banda de corte tem tolerância δ2, satisfazendo:
|H(ejw
)| ≤ δ2
A largura da banda de transição é:
∆w = wS - wP
Dado:
A = -20log10 δ,
considerando δ1 = δ2. Kaiser mostrou que:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-123-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 124
<
≤≤−+−
>−
=
21,0
5021,)21(07886,0)21(5842,0
50,)7,8(112,0
4,0
A
AAA
AA
β (Eq. 5.1)
Além disso, dados ∆w e A, M é aproximadamente:
w
A
M
∆
−
=
285,2
8
O procedimento para projetar um filtro passa-baixa digital FIR usando a janela
de Kaiser consiste nos seguintes passos:
i) Estabelecer as especificações wP, wS e δ.
ii) Estabelecer a frequência de corte wc do filtro passa-baixa ideal ao qual se
aplicará a janela (wc = (wP + wS)/2).
iii) Calcular A = 20log10 δ e ∆w = wP - wS e usar as fórmulas de Kaiser para
encontrar os valores de M e β.
iv) Encontra a resposta ao impulso do filtro através de h[n]=hd[n]w[n], onde w[n]
é a janela de Kaiser e hd[n] = ℑ-1
[Hd(ejw
)].
Devido à complexidade de cálculos com funções de Bessel, o projeto dessas
janelas não é fácil. A equação de w[n] definida por Kaiser tem valores
encontrados empiricamente e são definidos sem prova.
Exemplo: Projetar, usando janelas de Kaiser, um filtro passa-baixa com as
seguintes especificações: wP = 0,4π, wS = 0,6π e δ = 0,001.
wc = (wS + wP)/2 = 0,5π
∆w = wS - wP = 0,2π
A = -20log10 δ = 60 dB
Como A > 50, pela Eq. 5.1:
β = 0,1102(A – 8,7) ≅ 5,633](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-124-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 125
M = (A - 8)/(2,285∆w) ≅ 36,219 ⇒ M = 37 (M inteiro)
A resposta ao impulso é:
][
)2/(
)]2/([
][][][ nw
Mn
Mnwsen
nwnhnh c
d
−
−
==
π
com w[n] dado pela definição da janela de Kaiser.
Implementações no MatLab
O MatLab tem diversas funções para implementar janelas:
1. w = rectwin(M): Janela retangular
2. w = bartlett(M): Janela de Bartlett
3. w = hanning(M): Janela de Hanning
4. w = hamming(M): Janela de Hamming
5. w = blackman(M): Janela de Blackman
6. w = kaiser(M, beta): Janela de Kaiser
Antes de projetarmos alguns exemplos, vamos implementar duas funções base
importantes para os exemplos a seguir. Uma implementa uma resposta ao
impulso ideal de um filtro passa-baixa hd[n]. A outra função implementa a
plotagem no domínio da frequência, apresentando também a resposta em
magnitude absoluta e em escala dB (é uma variação da função freqz do
MatLab).
Função 1:
function hd = ideal_lp(wc, M)
% Ideal low pass filter
% wc = cutoff frequency
% M = length of the ideal filter
alpha = (M - 1)/2
n = [0:(M-1)];
m = n - alpha + eps;
hd = sin(wc*m)./(pi*m);](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-125-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 126
Função 2:
function [db, mag, pha, w] = freqz_m(b, a)
% Versao modificada da funcao freqz
[H, w] = freqz(b, a, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20*log10((mag + eps)/(max(mag)));
pha = angle(H);
Exemplo 1:
Projetar um filtro passa-baixa FIR com as seguintes especificações wP = 0,2π,
RP = 0,25 dB, wS = 0,3π e AS = 50 dB.
Tanto a janela de Hamming quanto a de Blackman provêem atenuação de mais
de 50 dB. Vamos escolher a janela de Hamming que provê a menor banda de
transição e assim tem a menor ordem.
wp = 0.2*pi; ws = 0.3*pi;
tr_width = ws - wp;
M = ceil(6.6*pi/tr_width) + 1
n = [0:M-1];
wc = (ws + wp)/2;
hd = ideal_lp (wc, M);
w_ham = (hamming(M))';
h = hd.*w_ham;
[db, mag, pha, w] = freqz_m(h, [1]);
delta_w = 2*pi/1000;
Rp = -(min(db(1:wp/delta_w+1)))
As = -round(max(db(ws/delta_w+1:501)))
subplot(1, 1, 1)
subplot (2, 2, 1); stem(n, hd); title('Resposta ao Impulso Ideal');
axis([0 M-1 -0.1 0.3]);xlabel('n');ylabel('hd[n]');
subplot (2, 2, 2); stem(n, w_ham); title('Janela de Hamming');
axis([0 M-1 0 1.1]);xlabel('n');ylabel('w[n]');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-126-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 127
subplot (2, 2, 3); stem(n, h); title('Resposta ao Impulso Atual');
axis([0 M-1 -0.1 0.3]);xlabel('n');ylabel('h[n]');
subplot (2, 2, 4); plot(w/pi, db); title('Magnitude em dB');grid
axis([0 1 -100 10]);xlabel('frequencia em pi unidades');ylabel('Decibeis');
M = 67
alpha = 33
Rp = 0,0394
As = 52
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-127-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 128
Exemplo 2:
Resolva o exemplo anterior usando uma janela de Kaiser.
wp = 0.2*pi; ws = 0.3*pi; As = 50;
tr_width = ws - wp;
M = ceil((As - 7.95)/(14.36*tr_width/(2*pi))+1) + 1
n = [0:M-1];
beta = 0.1102*(As - 8.7)
wc = (ws + wp)/2;
hd = ideal_lp (wc, M);
w_kai = (kaiser(M, beta))';
h = hd.*w_kai;
[db, mag, pha, w] = freqz_m(h, [1]);
delta_w = 2*pi/1000;
As = -round(max(db(ws/delta_w+1:501)))
subplot(1, 1, 1)
subplot (2, 2, 1); stem(n, hd); title('Resposta ao Impulso Ideal');
axis([0 M-1 -0.1 0.3]);xlabel('n');ylabel('hd[n]');
subplot (2, 2, 2); stem(n, w_kai); title('Janela de Kaiser');
axis([0 M-1 0 1.1]);xlabel('n');ylabel('w[n]');
subplot (2, 2, 3); stem(n, h); title('Resposta ao Impulso Atual');
axis([0 M-1 -0.1 0.3]);xlabel('n');ylabel('h[n]');
subplot (2, 2, 4); plot(w/pi, db); title('Magnitude em dB');grid
axis([0 1 -100 10]);xlabel('frequencia em pi unidades');ylabel('Decibeis');
M = 61
beta = 4,5513
alpha = 30
As = 52](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-128-320.jpg)
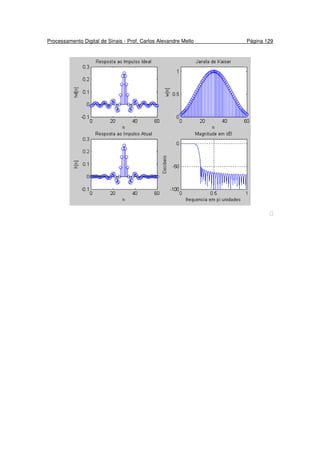
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 130
Exemplo 3:
Vamos projetar o filtro com as seguintes especificações (conforme a figura
abaixo):
Borda da banda de corte mais baixa: w1s = 0,2π, As = 60 dB
Borda da banda de passagem mais baixa: w1p = 0,35π, As = 1 dB
Borda da banda de corte mais alta: w2s = 0,65π, As = 1 dB
Borda da banda de passagem mais alta: w2p = 0,8π, As = 60 dB
Existem duas bandas de transição: ∆w1 = w1P – w1S, ∆w2 = w2S – w2P. Essas
duas larguras de banda devem ser a mesma no projeto da janela; i.e., não há
controle independente sobre ∆w1 e ∆w2. Assim ∆w1 = ∆w2 = ∆w1. Para esse
projeto, podemos usar a janela de Kaiser ou a de Blackman. Vamos escolher a
janela de Blackman. Vamos precisar também da resposta ideal ao impulso de
um filtro passa-faixa hd[n]. Observe que essa resposta ao impulso pode ser
obtida a partir de duas respostas em magnitude de filtros passa-baixa ideais,
considerando que elas tenham a mesma resposta em fase. Isso pode ser visto
na figura a seguir:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-130-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 131
ws1 = 0.2*pi; wp1 = 0.35*pi;
wp2 = 0.65*pi; ws2 = 0.8*pi;
As = 60;
tr_width = min((wp1-ws1), (ws2-wp2));
M = ceil(11*pi/tr_width) + 1
n = [0:M-1];
wc1 = (ws1 + wp1)/2;
wc2 = (ws2 + wp2)/2;
hd = ideal_lp(wc2, M) - ideal_lp(wc1, M);
w_bla = (blackman(M))';
h = hd.*w_bla;
[db, mag, pha, w] = freqz_m(h, [1]);
delta_w = 2*pi/1000;
Rp = -(min(db(wp1/delta_w+1:wp2/delta_w)))
As = -round(max(db(ws2/delta_w+1:501)))
subplot (2, 2, 1);
stem(n,hd); title('Resposta ao Impulso Ideal');
axis([0 M-1 -0.4 0.5]); xlabel('n'); ylabel ('hd[n]');
subplot (2, 2, 2); stem (n, w_bla); title ('Janela de Blackman');
axis ([0 M-1 0 1.1]); xlabel('n'); ylabel('w[n]');
subplot (2, 2, 3); stem(n, h); title('Resposta ao Impulso Atual');
axis([0 M-1 -0.4 0.5]);xlabel('n');ylabel('h[n]');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-131-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 132
subplot (2, 2, 4); plot(w/pi, db); title('Magnitude em dB');grid
axis([0 1 -150 10]);xlabel('frequencia em pi unidades');ylabel('Decibeis');
M = 75
alpha = 37
Rp = 0,0030
As = 75
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-132-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 133
Exemplo 4:
A resposta em frequência de um filtro passa-faixa ideal é dada por:
≤<
≤≤
<≤
=
ππ
ππ
π
||3/2,1
3/2||3/,0
3/||0,1
)(
w
w
w
eH jw
e
Usando uma janela de Kaiser, projete um filtro passa-faixa de comprimento 45
com atenuação na banda de corte de 60 dB.
Observe que a largura da banda de transição não foi dada. Ela será encontrada
a partir do comprimento M = 45 e do parâmetro β da janela de Kaiser. Das
equações de projeto da janela de Kaiser, podemos determinar β a partir de As:
)7,8(1102,0 −= SAβ
Vamos agora implementar a janela de Kaiser e observar a atenuação na banda
de corte.
M = 45; As = 60; n=[0:M-1];
beta = 0.1102*(As - 8.7)
w_kai = (kaiser(M, beta))';
wc1 = pi/3; wc2 = 2*pi/3;
hd = ideal_lp(wc1, M) + ideal_lp(pi, M) - ideal_lp(wc2, M);
h = hd.*w_kai;
[db, mag, pha, w] = freqz_m(h, [1]);
subplot (1, 1, 1);
subplot (2, 2, 1);
stem(n,hd); title('Resposta ao Impulso Ideal');
axis([0 M-1 -0.2 0.8]); xlabel('n'); ylabel ('hd[n]');
subplot (2, 2, 2); stem (n, w_kai); title ('Janela de Kaiser');
axis ([0 M-1 0 1.1]); xlabel('n'); ylabel('w[n]');
subplot (2, 2, 3); stem(n, h); title('Resposta ao Impulso Atual');
axis([0 M-1 -0.2 0.8]);xlabel('n');ylabel('h[n]');
subplot (2, 2, 4); plot(w/pi, db); title('Magnitude em dB');grid](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-133-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 134
axis([0 1 -80 10]);xlabel('frequencia em pi unidades');ylabel('Decibeis');
beta = 5,6533
Observe que, com esse valor, a mínima atenuação da banda de corte é menor
que 60 dB (observe que há lóbulos na banda de corte com pico acima de 60 na
escala negativa - ou seja, é menor que 60 em módulo – resposta em magnitude
na figura acima, destacada em vermelho). Assim, precisamos aumentar BETA
para aumentar a atenuação para 60 dB. Vamos colocar um acréscimo no valor
calculado de BETA para conseguir uma atenuação maior. Observamos que,
assim, a atenuação fica maior que 60 dB na banda de corte.
M = 45; As = 60; n=[0:M - 1];
beta = 0.1102*(As - 8.7) + 0.3
w_kai = (kaiser(M, beta))';](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-134-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 135
wc1 = pi/3; wc2 = 2*pi/3;
hd = ideal_lp(wc1, M) + ideal_lp(pi, M) - ideal_lp(wc2, M);
h = hd.*w_kai;
[db, mag, pha, w] = freqz_m(h, [1]);
subplot (1, 1, 1);
subplot (2, 2, 1);
stem(n,hd); title('Resposta ao Impulso Ideal');
axis([0 M-1 -0.2 0.8]); xlabel('n'); ylabel ('hd[n]');
subplot (2, 2, 2); stem (n, w_kai); title ('Janela de Kaiser');
axis ([0 M-1 0 1.1]); xlabel('n'); ylabel('w[n]');
subplot (2, 2, 3); stem(n, h); title('Resposta ao Impulso Atual');
axis([0 M-1 -0.2 0.8]);xlabel('n');ylabel('h[n]');
subplot (2, 2, 4); plot(w/pi, db); title('Magnitude em dB');grid
axis([0 1 -80 10]);xlabel('frequencia em pi unidades');ylabel('Decibeis');
beta = 5,9533
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-135-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 136
Exemplo 5:
A resposta em frequência de um filtro diferenciador digital ideal é dada por:
<<−−
≤<
=
0,
0,
)(
wjw
wjw
eH jw
d
π
π
Usando uma janela de Hamming de comprimento 21, projete um diferenciador
FIR. Plote as respostas no domínio do tempo e da frequência.
A resposta ao impulso de um diferenciador ideal com fase linear é dada por:
∫−
−−
=ℑ=
π
π
αα
π
dweeeHeeHnh jwnwjjw
d
wjjw
dd )(
2
1
])([][
∫∫
−
−
−
+−=
π
α
π
α
ππ 0
0
)(
2
1
)(
2
1
dweejwdweejw jwnwjjwnwj
=
≠
−
−
=
α
α
α
απ
n
n
n
n
,0
,
)(
)(cos
A resposta ao impulso acima pode ser implementada no MatLab através da
janela de Hamming para projetar o diferenciador requisitado. Note que se M é
um número par, então α = (M - 1)/2 não é um inteiro e hd[n] será zero para todo
n. Assim, M deve ser um número ímpar e teremos um filtro FIR de fase linear do
tipo III.
Para projetar um filtro FIR de fase linear (de qualquer tipo) usamos o código
abaixo:
function [Hr, w, coef, L] = Hr_Type(h, type)
% Calcula a resposta em ampiltude Hr[w] para filtros FIR tipo I, II, III e IV
% type = tipo de filtro
M = length(h);
if ((type == 1) | (type == 2))
L = (M - mod(type, 2))/2;
if (type == 1)
coef = [h(L+1) 2*h(L:-1:1)];](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-136-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 137
n = [0:L];
w = [0:500]'*pi/500;
Hr = cos(w*n)*coef';
else
coef = 2*[h(L:-1:1)];
n = [1:L]; n = n - 0.5;
w = [0:500]'*pi/500;
Hr = cos(w*n)*coef';
end
else
L = (M - mod(type, 2))/2;
if (type == 3)
coef = 2*[h(L+1:-1:1)];
n = [0:L];
w = [0:500]'*pi/500;
Hr = sin(w*n)*coef';
else
coef = 2*[h(L:-1:1)];
n = [1:L]; n = n - 0.5;
w = [0:500]'*pi/500;
Hr = sin(w*n)*coef';
end
end
Assim, podemos resolver a questão da seguinte forma:
M = 21; alpha = (M - 1)/2;
n = 0:M-1;
hd = (cos(pi*(n - alpha)))./(n - alpha);
hd (alpha + 1) = 0;
w_ham = (hamming(M))';
h = hd.*w_ham;
[Hr, w, P, L] = Hr_Type(h, 3);
subplot(1, 1, 1)
subplot (2, 2, 1); stem(n, hd); title('Resposta ao Impulso Ideal');
axis([0 M-1 -1.2 1.2]);xlabel('n');ylabel('hd[n]');
subplot (2, 2, 2); stem(n, w_ham); title('Janela de Hamming');
axis([0 M-1 0 1.2]);xlabel('n');ylabel('w[n]');
subplot (2, 2, 3); stem(n, h); title('Resposta ao Impulso Atual');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-137-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 138
axis([0 M-1 -1.2 1.2]);xlabel('n');ylabel('h[n]');
subplot (2, 2, 4); plot(w/pi, Hr/pi); title('Magnitude em dB');grid
axis([0 1 0 1]);xlabel('frequencia em pi unidades');ylabel('Slope in pi units');
Exemplo 6:
Projete um filtro transformador digital de Hilbert de comprimento 25 usando uma
janela de Hanning. A resposta em frequência ideal de um transformador de
Hilbert de fase linear é dada por:
<<−
<<−
= −
−
0,
0,
)(
wje
wje
eH wj
wj
jw
d
π
π
α
α
A resposta ao impulso ideal é dada por:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-138-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 139
=
≠
−
−
=
α
α
α
απ
π
n
n
n
nsen
nhd
,0
,
)(
]2/)([2
][
2
que pode ser implementado no MatLab. Como M = 25, o projeto do filtro é do
tipo III:
M = 25; alpha = (M - 1)/2; n = 0:M-1;
hd = (2/pi)*((sin((pi/2)*(n - alpha)).^2)./(n - alpha));
hd (alpha + 1) = 0;
w_han = (hanning(M))';
h = hd.*w_han;
[Hr, w, P, L] = Hr_Type(h, 3);
subplot (2, 2, 1); stem(n, hd); title('Resposta ao Impulso Ideal');
axis([0 M-1 -1.2 1.2]);xlabel('n');ylabel('hd[n]');
subplot (2, 2, 2); stem(n, w_han); title('Janela de Hamming');
axis([0 M-1 0 1.2]);xlabel('n');ylabel('w[n]');
subplot (2, 2, 3); stem(n, h); title('Resposta ao Impulso Atual');
axis([0 M-1 -1.2 1.2]);xlabel('n');ylabel('h[n]');
w = w'; Hr = Hr';
w = [-fliplr(w), w(2:501)]; Hr = [-fliplr(Hr), Hr(2:501)];
subplot (2, 2, 4); plot(w/pi, Hr); title('Resposta em Amplitude');grid
axis([-1 1 -1.1 1.1]);xlabel('frequencia em pi unidades');ylabel('Hr');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-139-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 140
5.1.2 Técnicas de Projeto por Amostragem em Frequência
Nessa técnica, usamos o fato de que a função de sistema H(z) pode ser obtida a
partir de amostras H(k) da resposta em frequência H(ejw
). Seja h[n] a resposta
ao impulso de um filtro FIR com M amostras, H[k] é sua transformada discreta
de Fourier com M-pontos (Capítulo 6) e H(z) sua função de sistema. Então
temos:
∑∑
−
=
−
−−
=
−
−
−
==
1
0
/21
1
0 1
][1
][)(
M
k
Mkj
MM
n
n
ez
kH
M
z
znhzH π
e
∑
−
=
−
−
−
−
=
1
0
/2
1
][1
)(
M
k
Mkjjw
jwM
jw
ee
kH
M
e
eH π (Eq. 5.2)
com](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-140-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 141
−=−
=
==
1,...,1,][*
0,]0[
)(][ /2
MkkMH
kH
eHkH Mkj π
Para um filtro FIR de fase linear temos:
h[n] = ±h[M – 1 - n], n = 0, 1, ..., M-1
onde o sinal positivo indica filtros FIR de fase linear dos tipos1 e 2 e o negativo é
para filtros FIR de fase linear dos tipos 3 e 4. Então H[k] é dado por:
][2
][ kHj
r e
M
k
HkH ∠
=
π
onde
−=
−
=
=
1,...,1,
)(2
0,]0[
2
Mk
M
kM
H
kH
M
k
H
r
r
r π
π
e
−+
−
=−
−
+
−
=
−
−
=∠
1,...,1
2
1
,)(
2
2
1
2
1
,...,0,
2
2
1
][
M
M
kkM
M
M
M
k
M
kM
kH
π
π
(para tipos 1 e 2)
ou
−+
−
=−
−
+
±−
−
=
−
−
±
=∠
1,...,1
2
1
,)(
2
2
1
2
2
1
,...,0,
2
2
1
2
][
M
M
kkM
M
M
M
k
M
kM
kH
ππ
ππ
(para tipos 3 e 4)](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-141-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 142
Dado um filtro passa-baixa ideal Hd(ejw
), escolha o filtro de comprimento M e
então amostre Hd(ejw
) em M igualmente espaçadas freqüências entre 0 e 2π. A
resposta H(ejw
) é a interpolação das amostras H[k] dadas pela Eq. 5.2 (Fig. 5.9).
A resposta ao impulso é dada por h[n] = TDF-1
(H[k]).
Fig. 5.9. Exemplo da técnica de amostragem em frequência.
Da Fig. 5.9, podemos observar que:
1) O erro de aproximação – a diferença entre a resposta ideal e a atual – é zero
nas freqüências amostradas.
2) O erro de aproximação nas outras freqüências depende da forma da resposta
ideal, ou seja, quanto mais “sharp” a resposta ideal, maior o erro de
aproximação.
3) O erro é maior perto das fronteiras das bandas e menor dentro das bandas.
5.1.3 Projeto Equirriple Ótimo
Os métodos de janelamento e de amostragem na frequência têm alguns
problemas:
1) Não podemos especificar wP e wS precisamente nos projetos.
2) Não podemos especificar δ1 e δ2 simultaneamente. Ou consideramos δ1 = δ2
(como no janelamento) ou otimizamos δ2 (como na amostragem).
3) O erro de aproximação não é distribuído uniformemente nas bandas. Ele é
mais alto perto das fronteiras das bandas e menor quanto mais distante delas.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-142-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 143
O método equirriple ótimo evita esses problemas. No entanto ele é bastante
difícil de utilizar e requer computador na sua implementação. O objetivo é
minimizar o erro máximo de aproximação (minimax do erro). Tais filtros são
chamados de equirriple porque o erro é distribuído de maneira uniforme na
banda de passagem e de corte o que resulta em um filtro de menor ordem.
No MatLab, um projeto por equirriple é feito usando a função remez que
implementa o algoritmo Parks-McClellan.
Exemplo:
Vamos projetar um filtro passa-baixa usando o algoritmo de Parks-McClellan. Os
parâmetros de projeto são:
wP = 0,2π, RP = 0,25 dB
wS = 0,3π, AS = 50 dB
wp = 0.2*pi; ws = 0.3*pi; Rp = 0.25; As = 50;
delta1 = (10^(Rp/20)-1)/(10^(Rp/20)+1);
delta2 = (1 + delta1)*(10^(-As/20));
deltaH = max(delta1, delta2);
deltaL = min(delta1, delta2);
weights = [delta2/delta1 1];
deltaf = (ws - wp)/(2*pi);
M = ceil((-20*log10(sqrt(delta1*delta2))-13)/(14.6*deltaf) + 1)
f = [0 wp/pi ws/pi 1];
m = [1 1 0 0];
h = remez(M - 1, f, m, weights);
[db, mag, pha, w] = freqz_m(h, [1]);
delta_w = 2*pi/1000;
wsi = ws/delta_w + 1;
Asd = -max(db(wsi:501))
while (Asd < As)](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-143-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 144
M = M + 1;
h = remez(M - 1, f, m, weights);
[db, mag, pha, w] = freqz_m(h, [1]);
delta_w = 2*pi/1000;
wsi = ws/delta_w + 1;
Asd = -max(db(wsi:501))
end
subplot (2, 1, 1); stem(h); title('Resposta ao Impulso Atual');
axis([0 M-1 -0.1 0.3]);xlabel('n');ylabel('h[n]');
subplot (2, 1, 2); plot(w/pi, db); title('Magnitude em dB');grid
axis([0 1 -100 10]);xlabel('frequencia em pi unidades');ylabel('Decibeis');
M = 43
Asd = 47.8404
M = 44
Asd = 48.2131
M = 45
Asd = 48.8689
M = 46
Asd = 49.8241
M = 47
Asd = 51.0857
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-144-320.jpg)

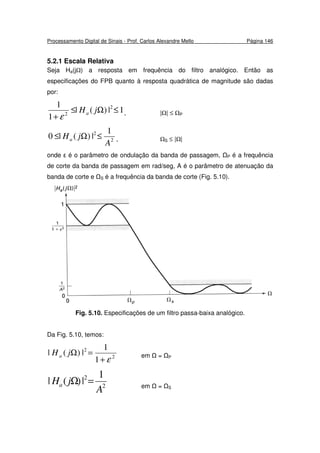

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 148
mapeia um sinal ou função em termos de vibrações (senóides), a transformada
de Laplace mapeia uma função em relação aos seus momentos:
∫
∞
∞−
−
= dtetftfL st
)()}({
onde s = σ + jω, com σ e ω números reais.
A transformada de Fourier é equivalente à transformada bilateral de Laplace
com argumento complexo s = jω.
Para um sinal amostrado x[n], a transformada de Laplace é dada por:
∑
∞
=
−
=
0
][)(
n
nsT
enxsX , onde T é o período de amostragem.
Essa relação expressa exatamente a transformada Z quando z = esT
. O
mapeamento do plano-s no plano-z pode ser visto na Fig. 5.11. Nesse diagrama,
linhas verticais no plano-s são mapeadas em ângulos no plano-z, enquanto
linhas horizontais são mapeadas em raios.
Fig. 5.11. Mapeamento do plano-s no plano-z.
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-148-320.jpg)
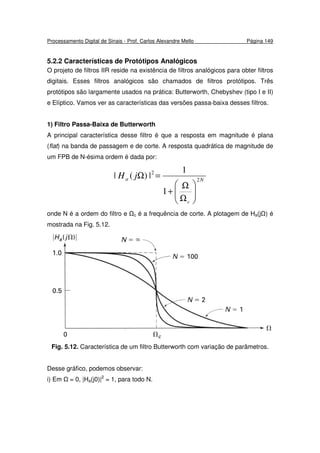

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 151
Resolvendo as equações para N = c, temos:
)/(log2
)]110/()110[(log
10
10/10/
10
SP
AR SP
N
ΩΩ
−−
=
Em geral, N não é um inteiro e, por isso, deve ser truncado para o menor inteiro
maior que o valor calculado: N = N. Obviamente, isso irá gerar um filtro com
ordem maior do que o necessário. Para satisfazer exatamente as especificações
do projeto em P:
N R
P
C
P2 10/
110 −
Ω
=Ω
ou para satisfazer exatamente as especificações em S:
N A
S
C
S2 10/
110 −
Ω
=Ω
Exemplo: Projete um filtro Butterworth satisfazendo:
Ponto de corte na banda de passagem: P = 0,2π
Ripple na banda de passagem: RP = 7 dB
Ponto de corte na banda de corte: S = 0,3π
Ripple na banda de corte: AS = 16 dB
Solução:
379,2
)3,0/2,0(log2
)]110/()110[(log
10
6,17,0
10
==
−−
=
ππ
N
Para satisfazer exatamente as especificações em P temos:
4985,0
110
2,0
3.2 7,0
=
−
=Ω
π
C](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-151-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 152
Para satisfazer exatamente as especificações em S temos:
5122,0
110
3,0
3.2 6,1
=
−
=Ω
π
C
Podemos escolher c entre esses dois valores, por exemplo c = 0,5. Temos
que projetar um filtro Butterworth com N = 3 e c = 0,5. Ou seja:
6
2
5,0
1
1
|)(|
Ω
+
=ΩjHa
Como = s/j, temos:
6666
2
641
1
21
1
5,0
1
1
|)(|
ss
j
S
sHa
−
=
−
=
+
=
cujos pólos podem ser calculados no MatLab (ou calculando pK, como antes):
>> a = [-64 0 0 0 0 0 1];
>> b = roots(a)
b =
-0.5000
-0.2500 + 0.4330i
-0.2500 - 0.4330i
0.5000
0.2500 + 0.4330i
0.2500 - 0.4330i](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-152-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 154
+
−
−
+
−
−
+
−
−
=
−
−
−
−
−
−
25,0
1
1
25,0
1
1
25,0
1
1
2
125,0
)(
1
12
1
1
1
1
z
z
z
z
z
z
zHa
A transformação bilinear pode ser ligada à fórmula trapezoidal para integração
numérica. Por exemplo, considere um filtro linear analógico com função de
transferência:
as
b
sH
+
=)( (Eq. 5.6)
Esse sistema pode ser caracterizado também pela equação de diferenças:
)(.)(.
)(
txbtya
dt
tdy
=+
Ao invés de substituir uma diferença finita pela derivada, suponha que
integramos a derivada e aproximamos a integral pela fórmula trapezoidal. Assim:
∫ +=
t
t
tydyty
0
)()(')( 0ττ
onde y’(t) denota a derivada de y(t). A aproximação da integral anterior pela
fórmula trapezoidal em t = nT e t0 = nT – T leva a:
[ ] )()(')('
2
)( TnTyTnTynTy
T
nty −+−+= (Eq. 5.7)
Agora, essa equação diferencial calculada em t = nT leva a:
)(.)(.)(' nTxbnTyanTy +−= (Eq. 5.8)
Usamos a Eq. 5.8 na Eq. 5.7 e obtemos a equação de diferenças para o sistema
discreto no tempo equivalente. Com y(n)≡ y(nT) e x(n)≡ x(nT), obtemos o
resultado:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-154-320.jpg)


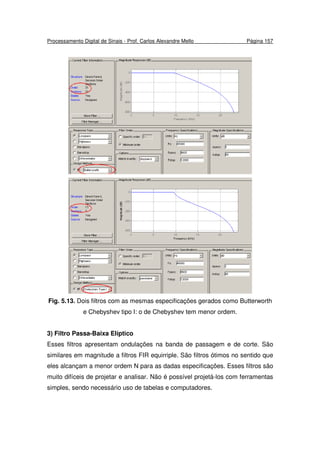







![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 165
3) Deslocamento na freqüência: f(t)ej2πw
0
t
→ F(w – w0)
4) Escalonamento: f(a.t) → (1/|a|)F(w/a)
5) Convolução no tempo: f(t)*g(t) → F(w).G(w)
6) Convolução na freqüência: f(t).g(t) → (1/2π)F(w)*G(w)
6.1 A Série Discreta de Fourier
Com o advento do computador digital, foi necessária uma adequação da
transformada para sinais de tempo discreto. Considere uma seqüência x[n] que
é periódica com período N, tal que x[n] = x[n + k.N], para qualquer inteiro k, e N
é o período fundamental da sequência. Da análise de Fourier, sabemos que
funções periódicas podem ser sintetizadas como uma combinação linear de
exponenciais complexas cujas freqüências são múltiplas (ou harmônicas) da
frequência fundamental (no caso 2π/N). Da periodicidade no domínio da
frequência da transformada de Fourier discreta no tempo, concluímos que existe
um número finito de harmônicos; as frequências {(2π/N)k, k = 0, 1, 2, ...., N-1}.
Assim, a sequência periódica x[n] pode ser expressa como:
∑
−
=
=
1
0
2
][
1
][
N
k
kn
N
j
ekX
N
nx
π
, n = 0, ±1, .... (Eq. 6.1)
onde {X[k], k = 0, ±1, ....} são chamados de coeficientes da série discreta de
Fourier, sendo dados por:
∑
−
=
−
=
1
0
2
][][
N
n
kn
N
j
enxkX
π
, k = 0, ±1, .... (Eq. 6.2)
onde x[n] é a seqüência discreta no domínio do tempo que descreve os valores
amostrados da variável contínua x(t) e N é o número de amostras da seqüência](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-165-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 166
da entrada. Observe que X[k] também é uma sequência periódica com período
fundamental igual a N. Ou seja, X[k + N] = X[k]. As equações 6.1 e 6.2 são a
representação discreta em série de Fourier de sequências periódicas.
Por conveniência de notação, podemos chamar:
WN = e-j(2π/N)
e assim o par de equações torna-se:
Equação de análise: ∑
−
=
=
1
0
][][
N
n
kn
NWnxkX
Equação de síntese: ∑
−
=
−
=
1
0
][
1
][
N
k
kn
NWkX
N
nx
Tanto x[n] quanto X[k] são seqüências periódicas.
Exemplo:
Encontre a representação em série de Fourier da sequência:
x[n] = {...0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, ....}
O período fundamental da sequência é N = 4. Assim, W4 = e-j2π/4
= e-jπ/2
= cos(-
π/2) + j.sen(-π/2) = 0 + j.(-1) = -j
Agora
∑=
=
3
0
4][][
n
kn
WnxkX
Assim:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-166-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 167
∑∑ ==
=+++===
3
0
3
0
.0
4 6]3[]2[]1[]0[][][]0[
nn
n
xxxxnxWnxX
De forma similar:
∑∑ ==
+−=−==
3
0
3
0
.1
4 22)]([][]1[
n
n
n
n
jjnxWnxX
∑∑ ==
−=−==
3
0
2
3
0
.2
4 2)]([][]2[
n
n
n
n
jnxWnxX
∑∑ ==
−−=−==
3
0
3
3
0
.3
4 22)]([][]3[
n
n
n
n
jjnxWnxX
Uma outra forma de ver a transformada discreta de Fourier é através de uma
representação em matrizes. Considere que x e X são vetores coluna
correspondendo aos períodos primários das sequências x[n] e X[k],
respectivamente. Então as equações de síntese e análise podem ser vistas
como:
X = WNx
e
x = (1/N)W*
NX
onde WN é dada por:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-167-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 168
A matriz WN é chamada de matriz DFS. Essa forma de calcular os coeficientes
da série discreta de Fourier pode ser implementado no MatLab da seguinte
forma:
function [Xk] = dfs (xn, N)
n = [0:1:N-1];
k = [0:1:N-1];
WN = exp(-j*2*pi/N);
nk = n'*k;
WNnk = WN.^nk;
Xk = xn*WNnk;
Por exemplo:
>> xn = [0 1 2 3]; N = 4;
>> Xk = dfs(xn, N)
Xk =6 -2 + 2i -2 - 0i -2 - 2i
Exatamente como calculamos anteriormente. A transformada inversa pode ser
obtida como:
function [xn] = idfs(Xk, N)
n = [0:1:N-1];
k = [0:1:N-1];
WN = exp(-j*2*pi/N);
nk = n'*k;
WNnk = WN.^(-nk);
xn = (Xk*WNnk)/N;
Para o Xk anterior, temos:
>> xn = idfs(Xk, N)
xn = 0 - 0i 1 - 0i 2 - 0i 3 + 0i.
Exemplo:
Considere uma sequência representando uma onda quadrada periódica:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-168-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 169
No MatLab:
>> L = 5; N = 20; k = [-N/2:N/2];
>> xn = [ones(1, L), zeros(1, N-L)];
>> Xk = dfs(xn, N);
>> magXk = abs([Xk(N/2+1:N) Xk(1:N/2+1)]); % DFS magnitude
>> stem(k, magXk); axis([-N/2, N/2, -0.5, 5.5]);xlabel('k'); ylabel('X[k]');
Para N = 40, temos:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-169-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 170
6.2 A Transformada Discreta de Fourier
Na prática, definimos a Transformada Discreta de Fourier (DFT) como o período
primário da DFS. Essa DFT é a transformada de Fourier para sequências
arbitrárias de duração finita.
Primeiro, definimos a squência de duração finita x[n] que tem N amostras sobre
0 ≤ n ≤ N – 1 como uma sequência de N-pontos. Seja x~ [n] um sinal periódico de
período N, criado usando uma sequência de N-pontos x[n]; isto é:
∑
∞
−∞=
−=
r
rNnxnx ][][~
O teorema da amostragem no domínio da frequência diz que, se x[n] é de
duração finita ([0, N-1]), então N amostras de X(z) no círculo unitário determinam
X(z) para todo z. Nesse sentido, N eqüidistantes amostras da transformada de
Fourier discreta no tempo X(ejw
) da sequência de N-pontos x[n] pode reconstruir
unicamente X(ejw
). Essas N amostras ao redor do círculo unitário são chamdas
de coeficientes da transformada discreta de Fourier. Seja X
~
[k] =DFS x~ [n], que é
uma sequência periódica (e assim de duração finita). Seu intervalo primário é
então a transformada discreta de Fourier, que é de duração finita. Essas noções](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-170-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 171
são claras na seguinte definição. A Transformada Discreta de Fourier de uma
sequência de N-pontos é dada por:
−≤≤
==
senão
NkkX
nxDFTkX
,0
10],[
~
])[(][
ou
∑
−
=
=
1
0
][][
N
n
kn
NWnxkX , 0 ≤ k ≤ N – 1
Note que X[k] também é uma sequência de N-pontos, ou seja, ela não é definida
fora do intervalo de 0 ≤ k ≤ N – 1.
A transformada discreta de Fourier inversa de uma DFT de N-pontos X[k] é dada
por:
])[(][ kXIDFTnx =
ou
∑
−
=
−
=
1
0
][
1
][
N
k
kn
NWkX
N
nx , 0 ≤ n ≤ N – 1
Novamente, x[n] não é definida fora do intervalo 0 ≤ n ≤ N – 1. A extensão de
x[n] fora desse intervalo é x~ [n].
Do início desse capítulo, fica claro que a DFS é praticamente equivalente à DFT
quando 0 ≤ n ≤ N – 1. Assim a implementação da DFT pode ser feita de forma
similar. Se x[n] e X[k] são organizados como vetores coluna x e X,
respentivamente, então temos:
X = WNx
e
x = (1/N)W*
NX](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-171-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 172
onde WN é a matriz DFS como antes. A implementação tanto da DFT quanto da
IDFT no MatLab é igual às da DFS e IDFS que apresentamos anteriormente.
Considere aquelas mesmas funções com nomes dft e idft apenas.
Uma outra possível representação da transformada discreta de Fourier é a forma
retangular que se utiliza da relação de Euler. A relação de Euler é dada por ejθ
=
cosθ + jsenθ . A DFT pode ser escrita então da seguinte forma:
∑
−
=
−
=
1
0
22
cos][][
N
n N
mn
jsen
N
mn
nxmX
ππ
lembrando que j = √−1. Este é um conceito abstrato conveniente para nos ajudar
a comparar a relação de fase entre várias componentes senóidais do sinal.
A DFT apresenta algumas propriedades que são muito úteis no processamento
digital de sinais, como: simetria, linearidade, deslocamento no tempo e
freqüência, entre outras. Fora a simetria, as outras propriedades são comuns à
transformada de Fourier de tempo contínuo.
6.3 Propriedades da Transformada Discreta de Fourier
1) Linearidade
Dadas duas seqüências periódicas com período N, x1[n] e x2[n], e suas
respectivas DFTs X1[k] e X2[k], então:
a.x1[n] + b.x2[n] ↔ a.X1[k] + b.X2[k]
Obs: Se x1[n] e x2[n] são sequências de durações diferentes (N1-pontos e N2-
pontos, por exemplo), escolha N3 = max(N1, N2). Se, por exemplo, N1 < N2, então
X1[k] é a DFT de x1[n] aumentada de (N2 – N1) zeros.
2) Deslocamento de uma seqüência
Seja x[n] uma seqüência periódica com coeficientes de Fourier X[m]. Assim:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-172-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 173
x[n – m] ↔ WN
km
X[m]
3) Dualidade
Se x[n] ↔ X[k]
então X[n] ↔ N.x[-k]
4) Simetria
A simetria pode poupar muito esforço computacional. Quando a seqüência do
sinal for real, então X[N − m]* = X[m]. Ou seja, basta que calculemos as
componentes de X[m] para 0 ≤ m ≤ N/2 .
Prova:
∑
−
=
−
=
1
0
2
][][
N
n
kn
N
j
enxkX
π
Logo
*
1
0
22*
1
0
)(
2
*
][][][
=
=− ∑∑
−
=
−−
=
−− N
n
nm
N
jnN
N
jN
n
mNn
N
j
eenxenxmNX
πππ
*
1
0
2
2*
][][
=− ∑
−
=
−
N
n
nm
N
j
nj
eenxmNX
π
π
onde e-j2πk
= cos(2πn) - jsen(2πn) = 1 – j.0 = 1. Assim:
*
1
0
2
*
][][
=− ∑
−
=
N
n
nm
N
j
enxmNX
π
Se x[n] for real:
][][][
1
0
2
*
mXenxmNX
N
n
nm
N
j
==− ∑
−
=
−
π
5) Convolução Periódica
∑
−
=
↔−
1
0
2121 ][][][][
N
m
kXkXmnxmx](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-173-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 174
onde o lado esquerdo da igualdade é conhecido como convolução, representado
por x1[n]*x2[n]. É importante observar que o somatório ocorre no intervalo 0 ≤ m
≤ N-1. O valor de x2[n – m] se repete periodicamente fora desse intervalo.
Exemplo:
>> n = 0:99;
>> fs = 200;
>> Ts=1/fs;
>>x=cos(2*pi*20*n*Ts + pi/4) + 3*cos(2*pi*40*n*Ts - 2*pi/5) + 2*cos(2*pi*60*n*Ts
+ pi/8);
>> X = fft(x);
>> m = 0:length(X) - 1;
>> subplot(3, 1, 1); stem(x); xlabel('n');ylabel('x(n)');title('Sequencia');
>> subplot(3, 1, 2); stem(m*fs/length(X), abs(X), 'b'); ylabel('magnitude');
>> xlabel('frequencia (Hz)'); title('Magnitude da Resposta em Frequencia');
>> subplot(3,1,3); stem(m*fs/length(X), angle(X), 'b'); ylabel('Angulo');
>> xlabel('frequencia (Hz)'); title('Fase');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-174-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 175
Observe que, como o sinal x[n] é real, a magnitude da resposta em frequência
apresenta uma imagem refletida. Assim, precisamos apenas da primeira metade
dela. Para a fase, o padrão também aparece refletido no eixo da freqüência;
novamente, só precisamos de metade da plotagem. Para a questão da
magnitude podemos fazer:
>> half_m = 0:ceil(length(X)/2);
>> stem(half_m*fs/length(X), abs(X(half_m + 1)), 'b');
>> ylabel('magnitude');
>> xlabel('frequencia (Hz)'); title('Magnitude da Resposta em Frequencia');
6.4 A Transformada Discreta Bi-Dimensional de Fourier
Para duas dimensões, a DFT e sua inversa podem ser vistas como:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-175-320.jpg)


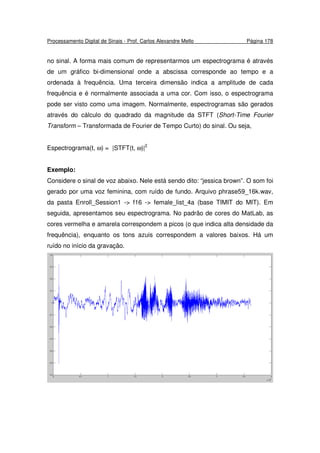
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 179
A função usada para gerar esse espectrograma pode ser vista abaixo:
% read the signal
[y,fs]=wavread('phrase59_16k.wav');
% calculate the table of amplitudes
[B,f,t]=specgram(y,1024,fs,256,192);
% calculate amplitude 50dB down from maximum
bmin=max(max(abs(B)))/300;
% plot top 50dB as image
imagesc(t,f,20*log10(max(abs(B),bmin)/bmin));
% label plot
axis xy; xlabel('Time (s)'); ylabel('Frequency (Hz)');
colormap(jet);
(fonte: http://www.phon.ucl.ac.uk/courses/spsci/matlab/lect9.html)
As figuras a seguir mostram as mesmas palavras ditas pela mesma mulher, mas
com outro tipo de microfone. Observe as diferenças mais visíveis no
espectrograma.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-179-320.jpg)
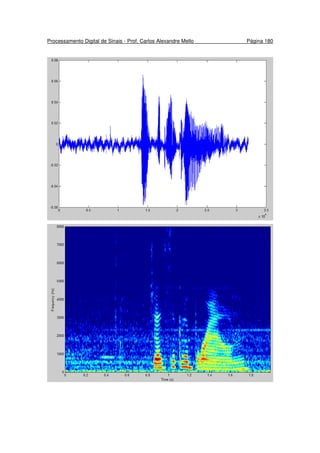
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 181
6.6 Exercícios
1. Determine os coeficientes da DFS das seguintes sequências periódicas,
usando a definição de DFS:
a) x1[n] = {2, 0, 2, 0}, N = 4
b) x2[n] = {0, 0, 1, 0, 0}, N = 5
c) x3[n] = {3, -3, 3, -3}, N = 4
d) x4[n] = {j, j, -j, -j}, N = 4
2. Determine as sequências periódicas, dados os seguintes coeficientes DFS,
usando a definição de IDFS:
a) X1[k] = {5, -2j, 3, 2j}, N = 4
b) X2[k] = {4, -5, 3, -5}, N = 4
c) X3[k] = {1, 2, 3, 4, 5}, N = 5
d) X4[k] = {0, 0, 2, 0}, N = 4
3. Seja x1[n] periódica com período fundamental N = 50, onde um período é
dado por:
≤≤
≤≤
=
−
4926,0
250,
][
3,0
1
n
nne
nx
n
e seja x2[n] periódica com período fundamental N = 100, onde um período é
dado por:
≤≤
≤≤
=
−
9926,0
250,
][
3,0
21
n
nne
nx
n
a) Encontre DFT{x1[n]} e plote (usando a função stem) os gráficos de sua
magnitude e de sua fase.
b) Encontre DFT{x2[n]} e plote (usando a função stem) os gráficos de sua
magnitude e de sua fase.
c) Qual a diferença entre as duas plotagens?](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-181-320.jpg)




![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 186
e = (a – b)d + a(c – d)
f = (a – b)d + b(c + d)
tendo 3 multiplicações apenas. O aumento na quantidade de adições não
prejudica o desempenho do algoritmo já que a multiplicação é o elemento mais
custoso.
7.2 Algoritmo de Cooley-Tukey ou Decimação no Tempo
J.W.Cooley (IBM) em colaboração com J.W.Tukey (Bell Labs) conseguiram uma
revolução maior no tratamento digital de sinais em 1965 com a publicação da
transformada rápida de Fourier, a FFT. Trata-se de um método engenhoso e
altamente eficiente de reagrupar os cálculos dos coeficientes de uma DFT. A
idéia é representar uma DFT de tamanho arbitrário N = N1.N2 em termos de
DFTs menores de tamanhos N1 e N2, procedendo recursivamente.
Lembrando que os coeficientes da DFT são definidos por:
∑∑
−
=
−
=
−
==
1
0
1
0
/2
][)]([)(
N
n
kn
N
N
n
knNj
WnxenxkX π
(Eq. 7.1)
onde k = 0, 1, 2, ...., N – 1. Calculada assim diretamente, a DFT requer O(N2
)
operações.
A idéia do algoritmo de Cooley-Tukey é dividir a seqüência x[n] em duas
seqüências: uma com os coeficientes de índice par e outra com os coeficientes
de índice ímpar. Como a quebra é em duas seqüências, o algoritmo é conhecido
também como Radix-2. Algoritmos no qual a seqüência é decomposta
sucessivamente em seqüências menores são chamados de algoritmos de
decimação em tempo.
O princípio do algoritmo de decimação em tempo pode ser analisado
considerando que N é um inteiro potência de 2, i.e., N = 2v
. Como N é um inteiro](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-186-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 187
par, podemos considerar calcular X(k), separando x[n] em duas seqüências de
N/2 pontos, consistindo dos pontos de índice par em x[n] e os pontos de índice
ímpar em x[n]. Como X(k) é dado pela Eq. 7.1, separando x[n] no pontos de
índice par e ímpar:
∑ ∑+=
parn ímparn
nk
N
nk
N WnxWnxkX
_ _
][][)(
Substituindo as variáveis n = 2r para n par e n = 2r + 1 para n ímpar:
∑∑
−
=
+
−
=
++=
12/
0
)12(
12/
0
2
]12[]2[)(
N
r
kr
N
N
r
rk
N WrxWrxkX (Eq. 7.2)
∑∑
−
=
−
=
++=
12/
0
2
12/
0
2
)](12[)](2[)(
N
r
rk
N
k
N
N
r
rk
N WrxWWrxkX (Eq. 7.3)
Mas WN
2
= WN/2 já que:
WN
2
= e-2j(2π/N)
= e-2j(π/(N/2))
= WN/2
Consequentemente, a Eq. 7.3 pode ser escrita como:
∑∑
−
=
−
=
++=
12/
0
2/
12/
0
2/ ]12[]2[)(
N
r
rk
N
k
N
N
r
rk
N WrxWWrxkX
][][)( kHWkGkX k
N+= (Eq. 7.4)](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-187-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 188
Cada parcela na Eq. 7.4 é reconhecida como uma DFT de N/2 pontos, sendo a
primeira parcela uma DFT de N/2 pontos dos pontos de índice par da sequência
original e o segundo termos uma DFT de N/2 pontos dos pontos de índice ímpar
da seqüência original. A Fig. 7.1 apresenta um diagrama de fluxo do cálculo de
uma DFT de 8 pontos.
Fig. 7.1. Decimação no tempo de uma DFT de N-pontos (N = 8) computada em
duas DFTs de N/2 pontos.
Na Fig. 7.1 duas DFTs de 4 pontos são calculadas, com G[k] designando a DFT
de 4 pontos dos termos de índice par e H[k] designando a DFT de 4 pontos dos
termos de índice ímpar. Na saída, X[0] é obtido multiplicando H[0] por WN
0
e
somando o produto com G[0]. X[1] é obtido multiplicando H[1] por WN
1
e
somando o resultado com G[1]. Para calcular X[4] deveríamos multiplicar H[4]
por WN
4
e somar o resultado com G[4]. Contudo, como G[k] e H[k] são](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-188-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 189
periódicas em k com período 4 (nesse caso), H[4] = H[0] e G[4] = G[0]. Assim,
H[4] é obtido multiplicando h[0] por WN
4
e somando o resultado com G[0]. Os
outros valores são obtidos de forma similar.
Com a computação re-estruturada de acordo com a Eq. 7.4, podemos analisar a
complexidade desse novo método e comparar com o algoritmo clássico da DFT.
A computação direta da DFT requer N2
multiplicações complexas e adições. A
Eq. 4 requer o cálculo de duas DFTs de N/2 pontos o que significa 2(N/2)2
multiplicações complexas e o mesmo número de adições, se usarmos o método
clássico para calcular cada DFT dessas. Então as duas DFTs de N/2 pontos
devem ser combinadas precisando N multiplicações complexas, correspondendo
a multiplicar H[k] pelo twiddle e N adições complexas para somar G[k] com o
resultado desse produto. Assim, a computação da Eq. 6.4 para todos os valores
de k requer, no máximo:
N + 2(N/2)2
= N + N2
/2
multiplicações complexas e adições. Para N> 2, esse valor é menor que as N2
operações necessárias pela DFT clássica.
A Eq. 7.4 corresponde a quebrar a computação da DFT de N-pontos em duas
DFTs de N/2 pontos. Se N/2 é par, o que acontece quando N é igual a uma
potência de 2, podemos considerar calcular cada DFT de N/2 pontos usando o
mesmo método. Assim, cada uma será quebrada em duas DFTs de N/4 pontos.
Com isso, G[k] e H[k] serão dados por:
∑∑
−
=
−
=
++=
14/
0
4/2/
14/
0
4/ ]12[]2[][
N
l
lk
N
k
N
N
l
lk
N WlgWWlgkG (Eq. 7.5)
∑∑
−
=
−
=
++=
14/
0
4/2/
14/
0
4/ ]12[]2[][
N
l
lk
N
k
N
N
l
lk
N WlhWWlhkH (Eq. 7.6)](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-189-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 190
Consequentemente, a DFT de N/2 pontos G[k] pode ser obtida combinando as
DFTs de N/4 pontos das sequências g[2l] e g[2l + 1]. O mesmo acontecendo
com o cálculo de H[k]. Assim, se as DFTs de 4 pontos da Fig. 7.1 forem
calculadas de acordo com as Eqs. 7.5 e 7.6, então o cálculo aconteceria como
na Fig. 7.2. Inserindo a computação da Fig. 7.2 no diagrama de fluxo da Fig. 7.1,
obtemos o diagrama completo da Fig. 7.3, onde expressamos os coeficientes
em termos de potências de WN ao invés de WN/2, considerando que WN/2 = WN
2.
Fig. 7.2. Gráfico de fluxo da decimação em tempo de uma DFT de N/2 pontos
em duas DFTs de N/4 pontos (para N = 8).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-190-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 191
Fig. 7.3. Fluxo completo do cálculo da DFT de 8 pontos, sendo dividida em 4 de
N/4 pontos.
Para a DFT de 8 pontos que estamos usando como exemplo, a computação foi
reduzida a DFTs de 2 pontos. A DFT de 2 pontos para, por exemplo, x[0] e x[4] é
detalhada na Fig. 7.4.
Fig. 7.4. Detalhe do cálculo de uma DFT de 2 pontos.
Para o caso geral, mas ainda considerando N como potência de 2, podemos
continuar com a decomposição da DFT de N/4 pontos em duas de N/8 pontos e
continuarmos até que só restem DFTs de 2 pontos. Como em uma árvore, esse](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-191-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 193
Fig. 7.5. Gráfico de fluxo de uma computação butterfly.
Fig. 7.6. Gráfico de fluxo de uma computação butterfly simplificada.
Em termos práticos, para desenvolver o cálculo apresentado na Fig. 7.3,
poderíamos usar dois arrays: um para o array sendo computado e outro para o
array usado na computação. Vamos denotar a seqüência de números
complexos resultante do m-ésimo estágio como Xm[l], onde l = 0, 1, ..., N-1, e
m=1, 2, ...., v. Além disso, vamos definir o conjunto de amostras de entrada
como X0[l]. Podemos pensar em Xm-1[l] como o array de entrada e Xm[l] como o
array de saída do m-ésimo estágio. Assim, para o caso de m = 8 como na Fig.
7.3:
X0[0] = x[0]
X0[1] = x[4]
X0[2] = x[2]
X0[3] = x[6]
X0[4] = x[1]
X0[5] = x[5]](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-193-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 194
X0[6] = x[3]
X0[7] = x[7]
Usando essa notação, podemos legendar a entrada e a saída do butterfly da Fig.
7.6, como indicado na Fig. 7.7, de acordo com as seguintes equações:
(Eqs. 7.7)
que podem ser re-escritas como:
(Eqs. 7.8)
Fig. 7.7. Gráfico de fluxo das Eqs. 7.8.
Pelas equações 7.8 e pela Fig. 7.3, está claro que apenas o passo m-1 é
necessário estar armazenado para poder calcular os valores do array no passo
m. Esse tipo de computação é chamado de computação in-place.
É importante observar também, pela Fig. 7.3, que a seqüência de entrada é
acessada de uma maneira não-sequencial. De fato, a ordem no qual os dados
de entrada são armazenados e acessados é chamada de ordem bit-reverso.
Para entendermos essa terminologia, a DFT de 8 pontos que vimos usando
como exemplo precisa de 3 bits para armazenar os índices dos dados.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-194-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 195
Escrevendo esses índices na forma binária, obtemos o seguinte conjunto de
equações:
X0[000] = x[000]
X0[001] = x[100]
X0[010] = x[010]
X0[011] = x[110]
X0[100] = x[001]
X0[101] = x[101]
X0[110] = x[011]
X0[111] = x[111]
Se (n2, n1, n0) é a representação binária do índice da seqüência x[n], então o
valor da seqüência x[n2, n1, n0] é armazenado no array na posição X0[n0, n1, n2],
invertendo os bits do índice n. Essa ordenação em subseqüências de índices
pares e ímpares é apresentada no diagrama em árvore da Fig. 7.8.
Outra forma de melhorar o desempenho do cálculo da DFT é através da
subdivisão da seqüência de saída. Esses algoritmos são chamados de
algoritmos de decimação em freqüência. Todo o processo é bem semelhante à
decimação em tempo.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-195-320.jpg)
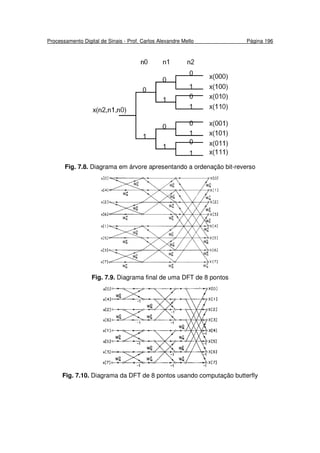





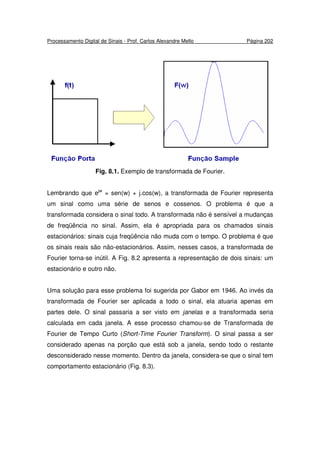
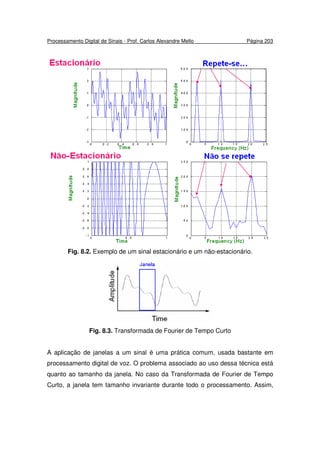

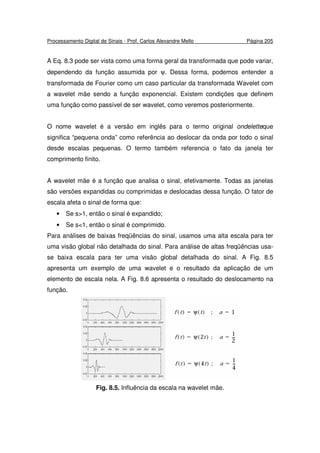

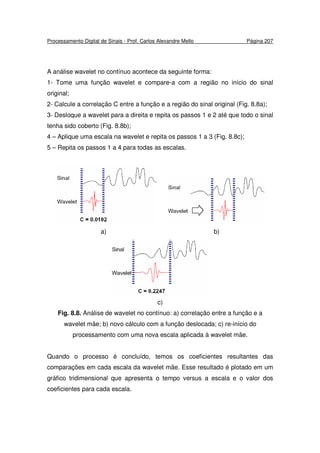




![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 212
A metade esquerda da Fig. 8.13 (filtros h0 e h1) corresponde à transformada
direta, chamada de análise. A metade da direita é a transformada inversa,
chamada de síntese. É esperado que a síntese gere um sinal de saída que seja
igual ao sinal de entrada.
Os filtros complementares de banco de filtros (h0 para h1 e g0 para g1) dividem o
sinal em sub-sinais de baixa e alta freqüência. Isso é chamado de subband
coding.
Para a transformada inversa, as saídas dos filtros da parte de análise (z[n] e
w[n]) passam por outros filtros FIR e, em seguida, são combinadas para gerar a
saída y[n]. A idéia é que w[n] e z[n] sejam versões transformadas de x[n] e que
y[n] é o sinal após a transformada inversa. Como dito anteriormente, espera-se
que y[n] seja igual a x[n].
Vamos considerar o filter bank da Fig. 8.14 e vamos ver como se comportam
w[n] e z[n].
Fig. 8.14. Exemplo de filter bank.
Na parte da análise, w[n] e z[n] são definidos por:
w[n] = a.x[n] + b.x[n – 1]
z[n] = b.x[n] – a.x[n – 1]
Precisamos saber também que são w[n – 1] e z[n – 1]:
w[n - 1] = a.x[n - 1] + b.x[n – 2]](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-212-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 213
z[n - 1] = b.x[n - 1] – a.x[n – 2]
Assim, y[n] será:
y[n] = -a.z[n] + b.z[n – 1] + b.w[n] + a.w[n – 1]
E, em relação ao sinal original:
y[n] = -a.( b.x[n] – a.x[n – 1]) + b.(b.x[n - 1] – a.x[n – 2]) + b.( a.x[n] +
b.x[n – 1]) + a.(a.x[n - 1] + b.x[n – 2])
y[n] = -ab.x[n] + aa.x[n – 1] + b.b.x[n - 1] – ba.x[n – 2] + b.a.x[n] +
b.b.x[n – 1] + a.a.x[n - 1] + ab.x[n – 2]
y[n] = aa.x[n – 1] + bb.x[n – 1] + bb.x[n – 1] + aa.x[n – 1]
y[n] = (2aa + 2bb).x[n – 1]
Essas operações retratam o processamento da wavelet de Haar. Essa é a mais
simples das wavelets. Se escolhermos com cuidado os coeficientes, teremos a
transformada de Haar. Por exemplo, se:
2aa + 2bb = 1
então
y[n] = x[n – 1]
ou seja, a saída é a entrada com um retardo de 1. Se procurarmos a e b tal que:
aa + bb = 1
podemos ter aa = ½ e bb = ½. Assim, se a = b = 1/√2, teremos os coeficientes
da transformada de Haar. A busca por coeficientes que tornem aa + bb = 1 e
não 2(aa + bb) = 1 está relacionada ao processo de downsampling como
explicado anteriormente.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-213-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 215
“mirror” vem do fato de que a magnitude da resposta em freqüência do filtro HPF
é uma imagem espelhada da magnitude da resposta em freqüência do filtro LPF.
Um das famílias de wavelets mais utilizadas é a família das Daubechies. Criada
por Ingrid Daubechies, a família das wavelets Daubechies (ou db) é a única
família de wavelets que tem suporte compacto e decaimento suave. O suporte
compacto impede que a wavelet se espalhe por todo o espectro. O decaimento
suave impede que a wavelet introduza artefatos de altas freqüências. Um
exemplo de uma wavelete de daubechies pode ser visto na Fig. 8.17.
Fig. 8.17. Forma de uma onda da família das Daubechies.
Vamos analisar o processamento de um sinal usando uma wavelet de 4
coeficientes e um conjugate quadrature filter conforme a Fig. 8.18.
Fig. 8.18. Um conjugate quadrature filter com quatro coeficientes.
Como foi feito anteriormente:
w[n] = a.x[n] + b.x[n – 1] + c.x[ n – 2] + d.x[n – 3]](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-215-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 216
z[n] = d.x[n] - c.x[n – 1] + b.x[ n – 2] - a.x[n – 3]
Considerando que:
w[n - k] = a.x[n - k] + b.x[n – k - 1] + c.x[ n – k - 2] + d.x[n – k - 3]
z[n - k] = d.x[n - k] - c.x[n – k - 1] + b.x[ n – k - 2] - a.x[n – k -3]
Se consideramos, nessas operações, que ac = -bd, então, chegamos à
expressão final:
y[n] = 2(aa + bb + cc + dd).x[n – 3]
Novamente, precisamos ter (aa + bb + cc + dd) = 1. Os coeficientes de
Daubechies obedecem a essas duas condições:
i) (aa + bb + cc + dd) = 1
ii) ac = -bd
8.4 Wavelets no MatLab
O MatLab traz uma série de ferramentas para lidar com wavelets. A mais básica
é a função swt (e swt2 para sinais bi-dimensionais como imagens) ou dwt. A
função swt permite diversos parâmetros de entrada (veja a documentação do
MatLab para ver todos), sendo os principais: o sinal de entrada, a quantidade de
níveis de decomposição e o tipo de wavelet (com o número de coeficientes
previamente calculados até certo ponto). Já a função dwt apresenta apenas a
decomposição do sinal nos componentes de aproximação e detalhes (como
apresentado na Fig. 8.11). A função wavemenu abre uma janela com diversas
funcionalidades do MatLab relacionadas com wavelets (Fig. 8.19). Todas essas
funções podem ser ativadas por linha de comando no próprio MatLab.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-216-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 217
Fig. 8.19. Tela do ambiente de processamento por wavelets do MatLab.
Exemplos:
1. Sinal de voz:
>> [som, Fz] = wavread(‘a_casa.wav’);
>> plot (som);
>> [cA1, cD1] = dwt(som, 'db1');
>> % reconstrução
>> l_s = length(som);
>> A1 = idwt(cA1,[ ],'db1',l_s);
>> D1 = idwt([ ],cD1,'db1',l_s);
>> subplot(2,1,1); plot(A1); title('Aproximacao A1');
>> subplot(2,1,2); plot(D1); title('Detalhes D1');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-217-320.jpg)
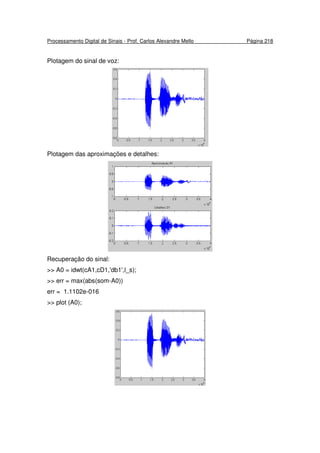
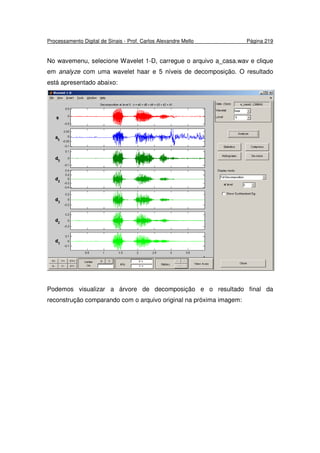
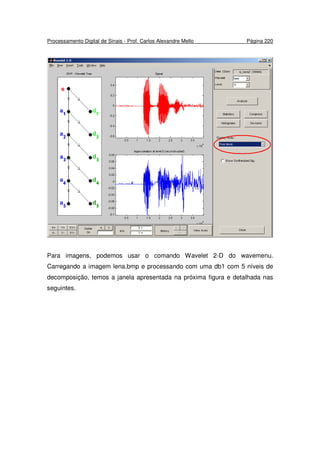
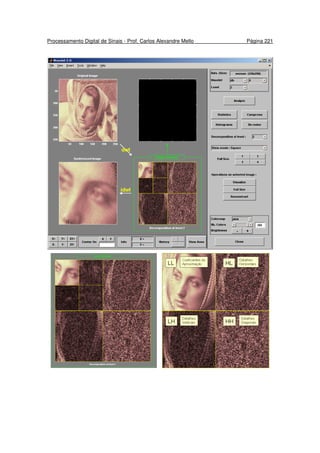

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 223
8.5 Exercícios
1.
a) Verifique se os coeficientes
a = (1-√3)/(4√2), b = (3-√3)/(4√2), c = (3+√3)/(4√2) e d = (1+√3)/(4√2)
podem ser coeficientes de uma wavelet de Daubechies.
b) Use esses coeficientes para filtrar a sequência:
x[n] = {8, 4, 0, 6, 3, 7, 2, 9}
de acordo com o filter banks da figura desta questão.
c) Agora, acrescente o downsampling antes das saídas z[n] e w[n] e um
upsampling após o processamento dessas saídas (antes da soma que gera
y[n]). Qual o erro entre a resposta da letra anterior e desta em relação à saída?
2. Para os coeficientes de filtros abaixo, use o MatLab para plotar a resposta em
frequência. Determine se os coeficientes correspondem a filtros passa-baixa,
passa-alta ou passa-faixa:
a) {-0.0884, 0.08840, 0.7071, 0.7071, 0.0884, -0.0884}
b) {-0.1294, 0.2241, 0.8365, 0.4830}
c) {-0.4830, 0.8365, -0.2241, -0.1294}](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-223-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 224
3. No conjugate quadrature filter da Figura 8.16, se a = 3 e b = 1, temos uma
transformada de Haar? Justifique.
4. Use o QMF da Figura 8.15 e encontre z, w e y para a = b = ½, dada a entrada
x[n] = {6, 1, 3, 7, 2, 5, 8, 10}.
5. Apresente as condições e exemplo de coeficientes para outra família de
wavelets.
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-224-320.jpg)


![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 227
Uma imagem digital pode ser entendida como uma função f(x,y), onde x e y são
as coordenadas espaciais e a função f é o nível de cinza (ou de brilho) naquele
ponto. Quando x, y e f estão numa escala finita e discreta, dizemos que temos
uma imagem digital.
A imagem digital pode ser gerada diretamente através de um dispositivo digital
ou pode ser digitalizada a partir de uma imagem real. Esse segundo caso é o
mais clássico, onde dispositivos, como scanners, por exemplo, faziam a
transposição da imagem do meio real para o digital. Para tanto, alguns
processos são fundamentais como veremos posteriormente.
Em termos de pesquisa e desenvolvimento, processamento digital de imagens
está inserido na grande área de processamento gráfico. Nessa área,
encontramos ainda elementos de computação gráfica e de visão computacional.
[Gomes e Velho, 1995] relacionam essas áreas de acordo com a representação
gráfica da Fig. 9.1. Essa representação e essa relação estão associadas ao tipo
de dado que entra e que sai de um sistema específico. Notadamente, essa
representação está relacionada com a percepção humana para os dados
inseridos e retornados pelos sistemas. Para os dispositivos, como
computadores, tudo é apenas processamento de dados.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-227-320.jpg)
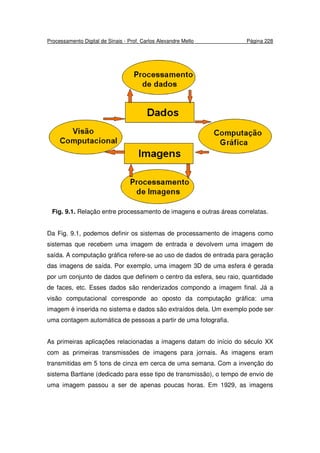

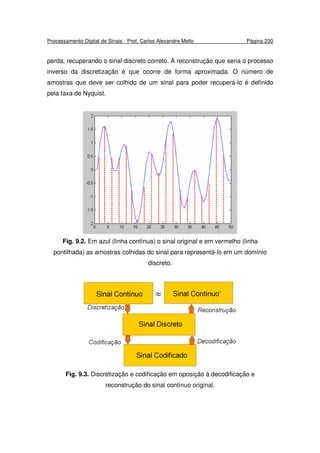
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 231
Tanto para sinais quanto para imagens, o processo de digitalização ocorre da
mesma forma. Em imagens, porém, ainda há outros elementos a serem
cuidados como será descrito posteriormente. Para geração do sinal (ou imagem)
discretizado, é preciso ter definido todo o modelo conceitual dos objetos em
estudo. Nesse caso, temos o que se chama [Gomes e Velho, 1995] do
Paradigma dos Quatro Universos (Fig. 9.4). Nele, temos o Universo Físico (que
são os objetos reais, como eles existem na natureza), o Universo Matemático
(que é uma descrição abstrata desses objetos), o Universo de Representação
(com descrições simbólicas dos objetos) e, por fim, o Universo de
Implementação (onde são associadas às descrições abstratas e simbólicas com
estruturas de dados implementáveis no computador). No caso, a imagem digital
é representada no computador através de uma matriz.
A matriz imagem tem suas dimensões definidas durante o processo de
digitalização. A coleta de amostras define qual será a dimensão da matriz. Essa
medida define a resolução da imagem e é especificada em dpi (dots per inch ou
pontos por polegada). A resolução da imagem não pode ser alterada após o
processo de digitalização a não ser por uma nova digitalização. Definida as
dimensões da matriz, define-se cada elemento dessa matriz. Em uma imagem
digital, o seu menor elemento, ou seja, a célula da matriz, é chamado de pixel.
Seu valor é definido também durante a digitalização em um processo
semelhante ao de amostragem chamado de quantização. Em uma analogia com
sinais, como fizemos na Fig. 9.2, a quantização é responsável por discretizar o
sinal em sua amplitude. Isso pode ser visto na Fig. 9.4. Nas imagens, a
amplitude de cada célula da matriz corresponde à sua cor. Assim, através da
quantização definimos quantas cores a imagem terá. A essa definição de cores
chama-se de resolução de cor da imagem. Diferente da resolução da imagem, a
resolução de cor, em alguns casos, pode ser alterada após a digitalização.
Dessa forma, uma imagem digital está completamente definida: suas dimensões
e a cor de cada pixel. Como está claro, então, uma imagem nada mais é do que](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-231-320.jpg)
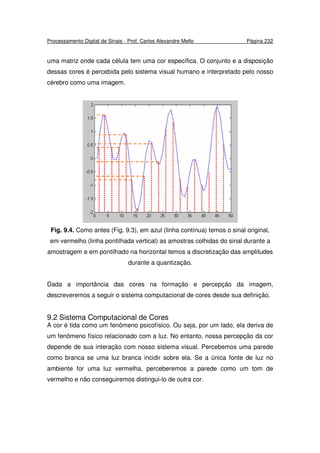









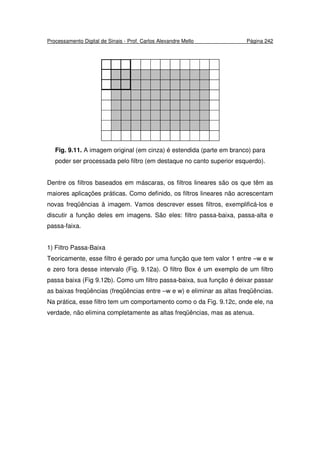
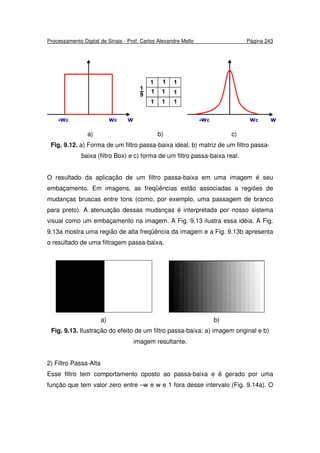
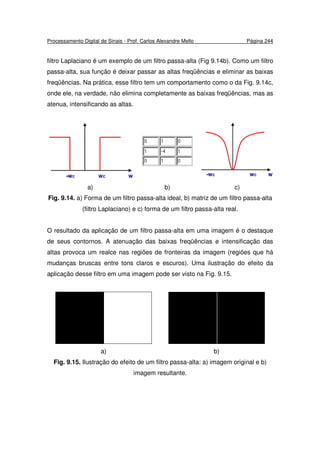
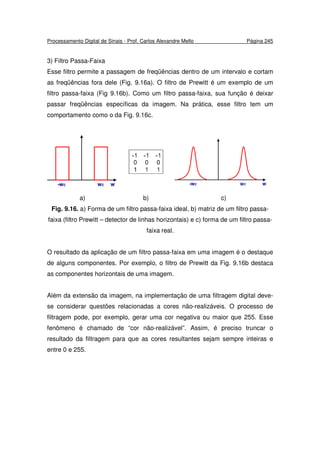
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 246
É possível também aplicar uma filtragem no domínio da frequência. Considere a
função abaixo no MatLab que calcula a transformada de Fourier de uma
imagem.
function [F] = img_fourier (nome, ext)
nome_in = [nome '.' ext];
im = imread(nome_in);
figure, imshow (im);
F = fft2(im);
figure;
F2 = fftshift(F);
imshow(log(abs(F2)), []);
colormap (jet);
O código acima pode ser complementado com as linhas abaixo para
implementar um filtro passa-baixas (gaussiano) e um filtro passa-alta
(laplaciano).
nx = size(F, 2);
ny = size(F, 1);
cxrange = [0:nx/2, -nx/2+1:-1];
cyrange = [0:ny/2, -ny/2+1:-1];
[cx, cy] = meshgrid(cxrange, cyrange);
fxrange = cxrange * 2*pi/nx;
fyrange = cyrange * 2*pi/ny;
[fx, fy] = meshgrid(fxrange, fyrange);
sigma = 0.3; % Gaussiana
ms = exp(-(fx.^2 + fy.^2)/(2*sigma^2));
smoothF = F.* ms;
smooth = ifft2(smoothF);
figure, imshow(smooth, []);
ftd = F.*fx.*i; % Diferenciacao
ftd(:, nx/2+1) = 0;
d = ifft2(ftd);
figure, imshow(d, []);
9.5 Compressão de Imagens
Como uma imagem é apenas uma matriz de dados, qualquer algoritmo de
compressão de dados pode ser usado para gerar compressão no arquivo
imagem. No entanto, podemos usar características da própria imagem para
alcançar mais altas taxas de compressão.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-246-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 248
Uma forma mais nova para gerar compressão é através do uso de wavelets. A
decomposição wavelet gera um downsampling em cada nível que, por definição,
já diminui a quantidade de dados. Assim, é bastante natural que ela seja usada
como mecanismo para gerar compressão.
9.6 Processamento de Imagens no MatLab
O MatLab possui uma toolbox específica para o tratamento de imagens digitais.
Essa toolbox possui diversos comandos para as diversas técnicas de
processamento de imagens. Pelas próprias características do MatLab, ele se
torna bastante apropriado para trabalhar com imagens. Por exemplo, a estrutura
básica do MatLab é a matriz e uma imagem nada mais é do que uma matriz.
Uma imagem é lida no MatLab e armazenada como uma matriz do tipo uint8.
Esse tipo armazena valores inteiros de 0 a 255 (correspondendo aos tons da
imagem), mas não podem ser usados com operadores de números do tipo
double como adição, subtração, multiplicação e divisão. Para tanto, é preciso
primeiro converter a matriz imagem para o tipo double.
O seguinte código apresenta diversas funções do MatLab para imagens na
prática:
>> im = imread (‘lena.jpg’); % Leitura da imagem em tons de cinza
>> [lin, col] = size(im); % lê o número de linhas e colunas de uma imagem
% e armazena nas variáveis lin e col (variáveis quaisquer)
>> imshow (im); % visualização de imagens
>> im2 = double(im); % conversão da imagem para tipo numérico
>> im2 = im2 + 10; % aumento do brilho de uma imagem
>> im2 = uint8(im2); % volta ao tipo imagem
>> imwrite (im2, ‘nome.bmp’, ‘bmp’); %salva a nova imagem
O código acima apresenta apenas um exemplo de trabalho com imagens. No
caso, uma imagem em tons de cinza é carregada e armazenada na variável im.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-248-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 249
Não há necessidade de indicar o tipo da imagem já que isso é lido direto do
cabeçalho da mesma. O MatLab aceita imagens do tipo bmp, jpg, tif, pcx e
alguns outros. A principal função desse código é a leitura do arquivo da imagem
com o comando imread. É possível esse comando ter dois argumentos de saída
quando queremos armazenar em uma variável a paleta de cores de uma
imagem (no caso de imagens com até 256 cores). Isso pode ser feito da forma:
[im, map] = imread(‘lena.bmp’);
Para imagens armazenadas no formato true color (24 bits) não há paleta de
cores. As matrizes R, G, B são armazenadas assim na imagem. Isso é tratado
no MatLab como uma matriz 3 dimensional. Cada dimensõ contém uma matriz
mxn que corresponde à matriz de um dos tons (exatamente na ordem RGB).
Para separar cada componente, o seguinte código pode ser utilizado:
>> im = imread(‘flowers.bmp’); % imagem 24 bits
>> r = im(:, :, 1); % atribui todas as linhas e todas as colunas do primeiro plano
% de im à variável r
>> g = im(:, :, 2); % matriz do segundo plano
>> b = im(:, :, 3); % matriz do terceiro plano
Nesse caso, observe que a leitura das dimensões da imagem deve ser feita
como:
>> [lin, col, plano] = size(im);
Ou seja, um terceiro parâmetro de saída deve ser usado. Podemos criar uma
nova imagem 24 bits fazendo:
>> im2 = uint8(zeros(lin, col, 3)); % criada uma imagem só de zeros
Cada plano dessa nova imagem pode receber os planos da outra imagem, por
exemplo:
>> im2(:, :, 1) = r;
>> im2(:, :, 2) = g;
>> im2(:, :, 3) = b;
Recorte de cores pode ser feito com os comandos:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-249-320.jpg)



























)12](
2
12[
2
cos(
12/
0
−=+++= ∑
−
=
nki
n
k
n
Sx
n
i
ik
π
DivX
O DivX é um codec de vídeo criado pela DivX, Inc. Ele foi produzido para ser
usado em compactação de vídeo digital, deixando os vídeos com qualidade,
apesar da alta compactação, utilizada para ocupar menos espaço no Disco
rígido. Para alcançar tal compactação é necessário muito processamento, o que
pode fazer com que um computador tecnologicamente defasado demore para](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-277-320.jpg)

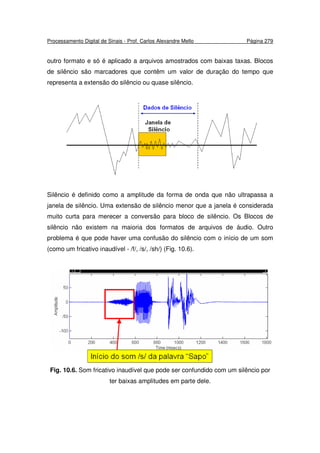





![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 285
>> mov = aviread('video1.avi', 3);
No caso, o 3º frame está sendo lido. Mas o arquivo de saída continua sendo um
arquivo de vídeo:
>> whos
Name Size Bytes Class Attributes
mov 1x1 230648 struct
Observe que a saída mov é do tipo struct.
>> mov
mov =
cdata: [240x320x3 uint8]
colormap: [ ]
>> mov1 = mov.cdata;
Agora, temos um arquivo de imagem que pode ser exibido como tal:
>> imshow (mov1)
Para exibição do vídeo podemos usar o comando movie:
>> movie(mov, repetições, info.FramesPerSecond);
O parâmetro repetições indica quantas vezes o vídeo será repetido.
A conversão de imagens para frame é feita com o comando im2frame:
>> mov1(i) = im2frame(imagem, map);](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-285-320.jpg)
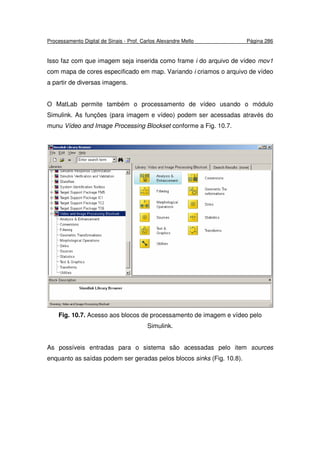
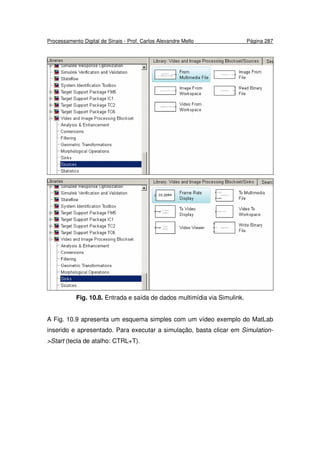

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 290
>> plot (som);
É comum precisarmos trabalhar com o arquivo de som normalizado. Para tanto,
usamos:
>> som = som/max(abs(som));
Isso não muda o sinal apenas o apresenta com amplitude entre -1 e 1.
A leitura de um arquivo wav pode ser feita com o comando wavread:
>> som = wavread (‘teste.wav’);
ou
>> [som, fs] = wavread (‘teste.wav’);
Nesse segundo caso, a frequência de amostragem do sinal é salva na variável
fs. O comando wavread não permite que o parâmetro de entrada seja uma
variável com o nome do arquivo. A entrada precisa ser especificamente o nome
do arquivo de som.
O processamento do sinal de áudio pode ser feito através de filtros como o
processamento de sinais, usando a função filter:
>> y = filter (b, a, som);
onde a e b são os coeficientes do filtro a ser aplicado (para filtros FIR, a = 1).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-290-320.jpg)
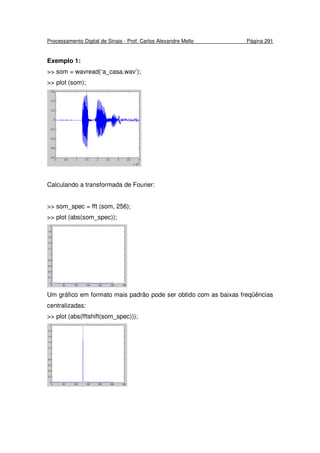
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 292
Suponha um filtro IIR com função de transferência: H(z) = 1 – 0,9375z-1
:
>> h = [1 -0.9375];
>> y = filter(h, 1, som);
>> soundsc(y, 22000);
Ouviremos um som mais nasal. Vamos fazer o mesmo processamento, mas
dividindo o som em amostras de 240 frames cada que serão filtradas
individualmente e re-agrupadas depois:
>> w = 240;
>> n = floor(length(som)/w);
>> for k=1:n
seg = som(1+(k - 1)*w:k*w);
segf = filter(h, 1, seg);
outsp(1+(k-1)*w:k*w) = segf;
end
>> soundsc(outsp, 22000);
Observem, a seguir (Fig. 10.13), a plotagem do sinal original (som) e filtrado
(outsp), assim como suas transformadas de Fourier:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-292-320.jpg)
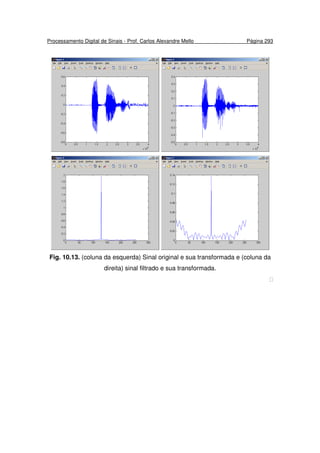
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 294
Exemplo 2: Como um exemplo da dificuldade de analisar um sinal que muda
constantemente, vamos construir um sinal “ágil na frequência” (um que muda
rapidamente suas características de frequência):
>> y = chirp([0:0.001:5],0,5,500);
>> soundsc (y); % Escute o som para entende-lo!!
>> z = [y, y(length(y):-1:1), y];
>> f = abs(fft(z, 8192));
>> plot(f(1:4096));
Mas esse gráfico representa mesmo o sinal que criamos? Vamos observar
melhor o sinal quebrando ele em janelas e plotando-as como uma “queda
d’água” (waterfall) para ver como as freqüências mudam pelo tempo.
>> s = spectrogram(z, 1024);
>> waterfall(abs(s)');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-294-320.jpg)

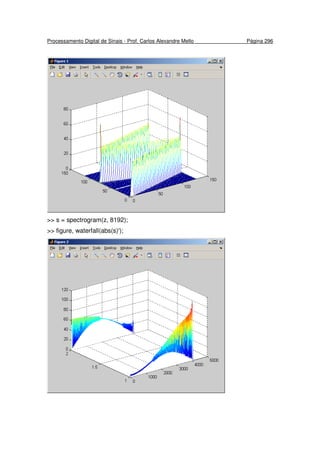

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 298
Usando essa informação, podemos criar diferentes notas no MatLab. Observe
que existem diferentes oitavas da mesma forma que existem diferentes teclas
em um piano. Aqui estão algumas no MatLab:
f = sin(2*pi*174.61*(0:0.000125:0.5));
g = sin(2*pi*195.99*(0:0.000125:0.5));
a = sin(2*pi*220*(0:0.000125:0.5));
b = sin(2*pi*246.94*(0:0.000125:0.5));
Pas de música faça:
line1 = [a,b,c,d,e,f];
line2 = [a,b,c,d,e,f];
As letras correspodem às notas que você cria no MatLab de acordo com a
tabela anterior. Coloque as notas na ordem que você quiser tocá-las. Para crier
uma música use:
song = [line1, line2];
e toque com sound() ou soundsc().](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-298-320.jpg)


![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 301
11. Processamento de Voz
O som é uma vibração que propaga pelas moléculas do ar até nossos ouvidos.
De uma forma geral, os sons são variações na pressão do ar ao longo do tempo
em freqüências que podemos ouvir. A voz é um tipo específico de som. Logo,
um som pode ser uma voz ou não. A voz consiste de um conjunto de sons que
podem ser gerados pelo ser humano. O sinal de voz pode ser plotado (Fig.11.1)
como uma forma de onda na qual podemos observar valores positivos e
negativos. Isso acontece porque a radiação de voz da boca faz com que a
pressão do ar seja temporariamente maior ou menor que a pressão do ar do
ambiente.
Fig. 11.1. Exemplo de plotagem de um sinal de voz.
O propósito primário da voz é comunicação. De acordo com a Teoria da
Informação conforme definida por Claude Shannon [Shannon, 1945], a voz pode
ser representada em termos de conteúdo ou informação. Outra maneira de
caracterizar o sinal de voz é como sendo uma onda acústica que carrega a
informação. Para o processamento de voz, o mais comum é entendermos o sinal
de voz como sendo uma onda ou algum modelo paramétrico como discutiremos
posteriormente.
A Informação gerada no cérebro é convertida em um conjunto de sinais neurais
os quais controlam o mecanismo articulatório (movimentos da língua, lábios,
cordas vocais, etc). As articulações movem-se em resposta a estes sinais
neurais para desempenhar uma seqüência de gestos os quais resultam em uma
forma de onda acústica que contém a informação da mensagem original.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-301-320.jpg)


![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 304
- Baixo custo;
- Permitem comunicação em canais ruidosos;
- Maior segurança de informação (permite inclusão de elementos de
criptografia).
O propósito do processamento digital pode ser:
• Saber se determinado sinal corresponde a um sinal de voz ou não
• Classificar uma seção de um sinal de voz como:
o voz audível (voiced speech)
o voz inaudível (unvoiced speech)
o silêncio ou ruído de fundo
• Redução de ruído
Para redução de ruído, por exemplo, a filtragem digital do sinal usando filtros FIR
ou IIR pode trazer bons resultados. Vejamos o exemplo a seguir. Dado o sinal
de voz abaixo:
Trata-se de um sinal de voz ruidoso contendo a expressão “a casa” com um
ruído de fundo. Esse sinal pode ser filtrado com a redução do ruído através do
uso de uma janela de Hanning conforme o código:
[y, fs] = wavread('casa1.wav');
b = fir1(98, 31/80, hanning(99));
filt_sp=filter(b,1,y);
f = 0:8000/(127):8000;
subplot(2,1,1)
spect=fft(y, 256);
plot(f, abs(spect(1:128)))/max(abs(spect(1:128)));](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-304-320.jpg)
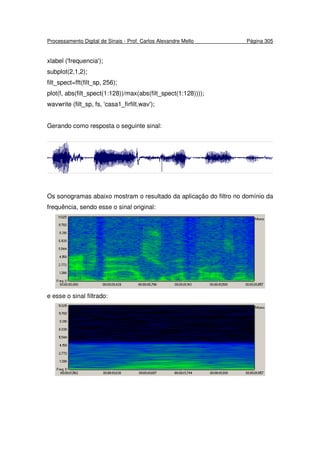


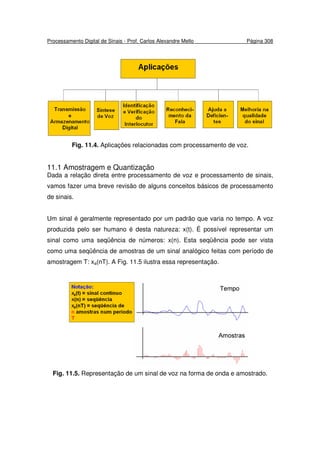
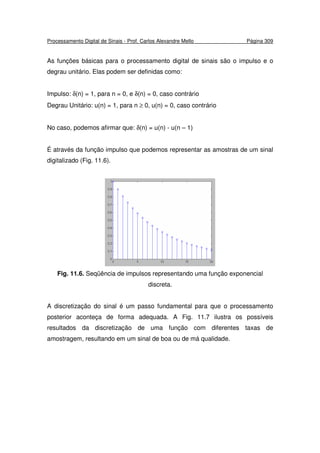
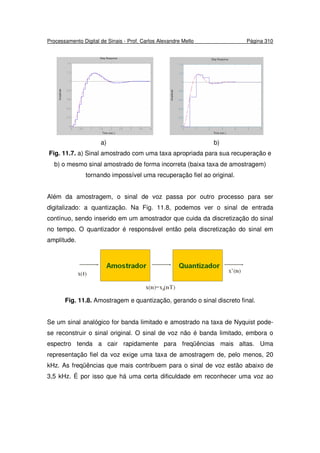


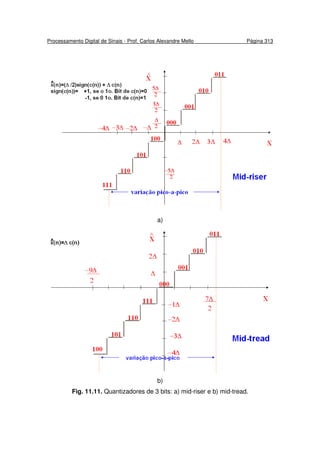
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 314
Companding é uma expressão que significa compress + expand. Para tornar a
porcentagem de erro constante os níveis de quantização devem ser espaçados
logaritmicamente. Para tanto, o logaritmo da entrada é quantizado ao invés da
própria entrada:
y(n) = ln|x(n)|
Cujo inverso é:
x(n) = exp[y(n)]sgn[x(n)]
Dessa maneira, pode-se mostrar que o nível sinal-ruído é independente da
variância do sinal. Problemas acontecem com pequenas amplitudes (x[n] ≈ 0). A
Fig. 11.12 apresenta em diagrama de blocos como se desenvolve a codificação
e a decodificação do sinal.
Fig. 11.12. Representação da técnica de companding.
O problema da quantização é quanto a quantidade de degraus. Desejamos fazer
essa quantidade suficientemente grande para termos uma varredura pico-a-pico
do sinal. Mas isso implica mais níveis de quantização. Porém, mais níveis de
quantização implica em uma cpdificação com mais bits o que implica em maior
tempo de processamento/espaço de armazenamento; o que não é interessante.
Esse é o grande dilema.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-314-320.jpg)


o sinal de voz, x(.), é submetido a transformação T[ ], linear ou não, a qual pode
depender de um conjunto ajustável de parâmetros.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-316-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 317
Observando a Eq. 11.1, podemos vê-la como uma operação de convolução da
transformação do sinal de entrada x() por uma função w. Aqui, podemos
entender w como uma seqüência de janelas posicionadas em um tempo
correspondente a amostra índice n (Fig. 11.14). O produto é somado sobre
todos os valores diferentes de zero. Geralmente, w é de duração finita, mas
pode ser infinita.
Fig. 11.14. Processamento de um sinal de voz em uma janela w.
11.2.1 Energia de Curta Duração
Das técnicas temporais para processamento de voz a mais simples é a Energia
de Curta-Duração. A amplitude do sinal de voz varia apreciavelmente com o
tempo. A voz audível apresenta amplitude maior que a voz inaudível ou o
silêncio (ruído de fundo), assim, a energia de curta duração de um sinal provê
uma representação conveniente que reflete as variações de amplitude. A
energia de um sinal discreto no tempo pode ser definida como:
∑
∞
−∞=
=
m
mxE )(2
Em relação à equação de Qn (Eq. 11.1), temos:
T[ ] = quadrado
w(n) = 1, 0 ≤ n ≤ N – 1 e 0, caso contrário.
A energia de tempo curto de um sinal de voz pode ser definida como:](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-317-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 318
∑
∞
−∞=
−=
m
n mnwmxE 2
)]().([
que pode ser re-escrita como:
∑
∞
−∞=
−=
m
n mnhmxE )(.)( 2
com h(n) = w2
(n). Observamos que En é um número e não uma função.
Um problema relacionado ao processamento em tempo curto é o tamanho da
janela. Para o caso da Energia, por exemplo, se a janela for muito longa e
constante em amplitude, En varia muito pouco em relação ao tempo. Essa janela
seria equivalente a um filtro de passa-baixa de banda (muito) estreita. Uma
janela estreita demais não consegue produzir uma função suave de energia. Se
a janela for muito estreita, não proverá medições suficientes para produzir uma
função de energia suave. Se a janela for da ordem de vários picos do sinal, En
não vai refletir as variações do sinal. Esse conflito é de grande importância na
representação em tempo curto de sinais de voz.
Dessa maneira o tamanho da janela varia desde:
a) 20 amostras para uma voz aguda de mulher ou criança;
b) 250 amostras para uma voz grave de homem.
Na prática, para uma freqüência de amostragem do sinal de 10 kHz deve-se
utilizar uma janela da ordem de 100 < N < 200 amostras (10 ms < t < 20 ms).
A maior significância de En está em conseguir distinguir entre segmentos com
voz audível e voz inaudível. Os valores de En são significativamente maiores
para sinais audíveis. En pode ser usada para determinar o tempo onde um sinal
audível torna-se inaudível e vice-versa; se o sinal for de boa qualidade pode-se
distinguir a voz do silêncio.](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-318-320.jpg)


![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 321
Fig. 11.16. Uma senóide tem duas passagens pelo zero em um ciclo.
Os sinais de voz são sinais faixa-larga e, portanto, a interpretação da taxa média
de passagem pelo zero é menos precisa. Estimativas grosseiras das
propriedades espectrais podem ser obtidas baseadas na taxa de passagem pelo
zero média em tempo curto.
Pode-se definir:
∑
∞
−∞=
−−−=
m
n mnwmxmxz )(|)]1(sgn[)](sgn[|
onde
sgn[x(m)] = 1, se x(n) ≥ 0
= -1, se x(n) < 0
e
w(n) = 1/(2N), para 0 ≤ n ≤ N-1
= 0, caso contrário
O modelo para a produção da fala sugere que a energia dos sinais de voz está
concentrada abaixo de 3 kHz (340 Hz a 4 KHz) devido ao corte produzido pela
onda produzida na glote. A maior parte da energia para sinais de voz não
audíveis é de alta-freqüência: altas freqüências implicam uma taxa alta de
passagem pelo zero e baixas freqüências implicam numa taxa baixa de
passagem pelo zero. Assim, há uma correlação forte entre taxa de passagem](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-321-320.jpg)

![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 323
A representação em função de autocorrelação de um sinal é um modo
conveniente de apresentar algumas propriedades do sinal. Por exemplo, se o
sinal é periódico com período de P amostras, então:
φ(k) = φ(k+P)
Ou seja, a autocorrelação de uma função periódica também é periódica com o
mesmo período. Outras propriedades importantes da função de autocorrelação
são:
1) Ela é uma função par: φ(k) = φ(-k);
2) Ela alcança seu valor máximo quando k = 0; i.e.; |φ(k)|≤0, para todo k;
3) O valor de φ(0) é igual à Energia para sinais determinísticos ou à potência
média para sinais periódicos.
A função de autocorrelação para tempo curto é definida como:
∑
∞
−∞=
−−+−=
m
n mknwkmxmnwmxkR )()()()()(
Ou seja, primeiro, um segmento de voz é selecionado pelo produto com a janela;
em seguida, a autocorrelação é aplicada ao segmento de voz sob a janela. A
técnica de autocorrelação pode ser usada para estimativa do pitch (frequência
fundamental) de um sinal de voz. O seguinte código do MatLab pode ser usado
para estimar a frequência fundamental de um sinal usando a função de
autocorrelação:
[x,fs]=wavread('casa1.wav');
ms20=fs/50; % minimum speech Fx at 50Hz
%
% plot waveform
t=(0:length(x)-1)/fs; % times of sampling instants
subplot(2,1,1);
plot(t,x);
legend('Waveform');](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-323-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 324
xlabel('Time (s)');
ylabel('Amplitude');
%
% calculate autocorrelation
r=xcorr(x,ms20,'coeff');
%
% plot autocorrelation
d=(-ms20:ms20)/fs; % times of delays
subplot(2,1,2);
plot(d,r);
legend('Autocorrelation');
xlabel('Delay (s)');
ylabel('Correlation coeff.');
% Estimativa da frequencia fundamental
ms2=fs/1000; % maximum speech Fx at 1000Hz
ms20=fs/50; % minimum speech Fx at 50Hz
% just look at region corresponding to positive delays
r=r(ms20+1:2*ms20+1);
[rmax,tx]=max(r(ms2:ms20));
fprintf('rmax=%g Fx=%gHzn',rmax,fs/(ms2+tx-1));
Podemos ver a aplicação desse código no sinal de voz correspondente ao som
“a casa”. Nesse caso, a frequência fundametal estimada é:
Fx=512.195Hz](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-324-320.jpg)
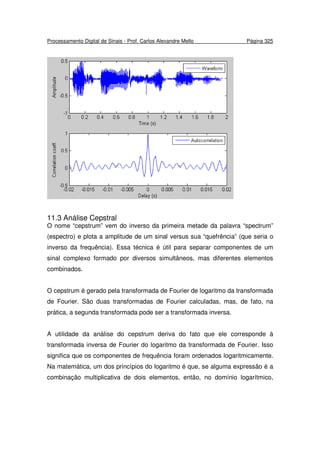
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 326
esses elementos são combinados aditivamente. Colocando de outra forma, se o
sinal sob análise y(t) é igual a h(t) vezes x(t):
y(t) = h(t).x(t)
então:
log[y(t)) = log[h(t)] + log[x(t)]
No domínio do processamento digital de voz, x(t) pode ser o pitch enquanto h(t)
é o componente do trato vocal.
A quefrência é uma medida de tempo, embora não no sentido de um sinal no
domínio do tempo. Por exemplo, se a taxa de amostragem de um sinal de áudio
é 44100 Hz e existe um pico no gráfico do cepstrum cuja quefrência é 100
amostras, o pico indica a presença de um pitch que é 44100/100 = 441 Hz. Esse
pico ocorre no cepstrum porque os harmônicos no espectro são periódicos e o
período corresponde ao pitch. O código de MatLab abaixo estima a frequência
fundamental do arquivo ‘casa1.wav’:
[x,fs]=wavread('casa1.wav');
ms1=fs/1000; % máxima frequência de voz Fx em 1000Hz
ms20=fs/50; % mínima frequência de voz Fx em 50Hz
%
% plotagem da forma de onda
t=(0:length(x)-1)/fs;
subplot(3,1,1);
plot(t,x);
legend('Waveform');
xlabel('Time (s)');
ylabel('Amplitude');
Y = fft(x);
% plotagem do espectro abaixo de 5000Hz
hz5000=5000*length(Y)/fs;
f=(0:hz5000)*fs/length(Y);](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-326-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 327
subplot(3,1,2);
plot(f,20*log10(abs(Y(1:length(f)))+eps));
legend('Spectrum');
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
% cepstrum
C=fft(log(abs(Y)+eps));
% plotagem entre 1ms (=1000Hz) e 20ms (=50Hz)
q=(ms1:ms20)/fs;
subplot(3,1,3);
plot(q,abs(C(ms1:ms20)));
legend('Cepstrum');
xlabel('Quefrency (s)');
ylabel('Amplitude');
[c,fx]=max(abs(C(ms1:ms20)));
fprintf('Fx=%gHzn',fs/(ms1+fx-1));
Frequência estimada: 667.171Hz](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-327-320.jpg)
![Processamento Digital de Sinais - Prof. Carlos Alexandre Mello Página 328
Outra aplicação do cepstrum é a extração da informação de envelope para
análise da voz. Em geral, o envelope espectral é uma forma mais suave do
gráfico da frequência, onde o processo de suavização ignora os componentes
de mais alta frequência. No domínio cepstral, isso corresponde ao descarte de
todos os coeficientes cepstrais relacionados às frequências maiores que o
envelope da frequência. Isso pode ser conseguido no MatLab com o código
abaixo:
[som, fs] = wavread('casa1.wav');
ps = log(abs(fft(som)));
len = length(som);
cep = ifft(ps);
% Filtragem
cut = 30;
cep2 = zeros(1, len);
cep2(1:cut-1) = cep(1:cut-1)*2;
cep2(1) = cep(1);
cep2(cut) = cep(cut);
% Converte para o dominio da frequencia
env = real(fft(cep2));
act = real(fft(cep));
pl1 = 20*log10(env(1:len/2));
pl2 = 20*log10(act(1:len/2));
span = [1:fs/len:fs/2];
pl1(length(pl1)) = [];
pl2(length(pl2)) = [];
plot (span, pl1, 'k-.'); figure, plot(span, pl2, 'g');
Na figura a seguir temos o cepstrum (em verde) e o envelope (em preto).](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-328-320.jpg)
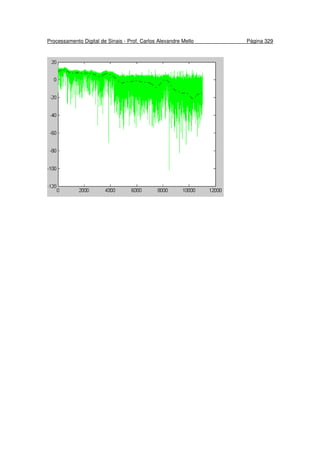
 Cite quais os cuidados que devem ser tomados na definição da
janela w(n).
2. Diferencie Quantização e Amostragem, relacionando as duas técnicas com o
processo de Digitalização de um sinal. É correto afirmar que a quantização
de um sinal pode compactá-lo? Essa compactação seria com ou sem perda
de informação?
3. Construa o gráfico da função característica do quantizador de 2 bits definido
pela seguinte relação entre as amostras quantizadas e a palavra código:
2/*)1)((*))((
^
∆+= ncncsignx
onde a função sign(c(n)) é igual a +1, se o primeiro bit de c(n) for igual a
zero, e igual a –1, se o primeiro bit de c(n) for 1. Para c(n) é usada uma
representação em sinal-magnitude. Tal quantizador possui características de
um quantizador mid-riser? E mid-tread?
](https://image.slidesharecdn.com/pds-140721225020-phpapp01/85/Processamento-de-Sinais-330-320.jpg)
