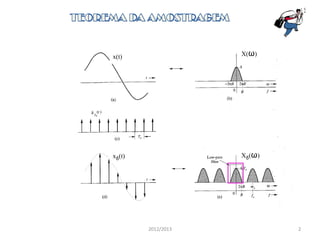
1) O documento discute amostras de sinais, transformada de Fourier discreta e FFT. 2) O teorema da amostragem estabelece que um sinal limitado em frequência pode ser completamente descrito pelos seus valores de amostragem se a taxa de amostragem for maior que o dobro da largura de banda do sinal. 3) A transformada de Fourier discreta calcula amostras de um sinal na frequência a partir das amostras no domínio do tempo, resultando em um número finito de valores de frequência.

1. 2012/2013
1

2. 2012/2013
x(t)
xδ(t)
X(ω)
Xδ(ω)
2

3. 1
( ) ( )
S
X f X f
T
 
O teorema da Amostragem diz que para uma sinal limitado na frequência com largura
de banda limitada B pode ser completamente descrito pelos valores das suas amostras
usando um período de amostragem Ts desde que
Dem:
Trasf. de Fourier
Relação entre a TF do sinal analógico e a TF
discreta do sinal amostrado
[1]
[1]
𝑻 𝑺 ≤ 𝟏/(𝟐𝑩)
𝒇 𝒔 = 𝟏/𝑻 𝒔 = 𝟐𝑩 é 𝒅𝒆𝒔𝒊𝒈𝒏𝒂𝒅𝒂 𝒑𝒐𝒓 𝒇𝒓𝒆𝒒𝒖ê𝒏𝒄𝒊𝒂 𝒅𝒆 𝑵𝒚𝒒𝒖𝒊𝒔𝒕

4. 2012/2013
A transformada de Fourier Discreta é feita numericamente, a partir das
amostras da função g(t) o que faz com que seja calculada G(ω) apenas num
nº finito de frequências- amostras de G(ω)
Dado que na computação numérica o nº de dados tem que ser finito o sinal
g(t) tem que ser limitado no tempo, se tal não acontecer o sinal tem que ser
truncado. O mesmo se passa com o sinal na frequência.
4

5. 2012/2013
O número de amostrar N0 é dado por: 𝑁0 =
𝑇0
𝑇𝑠
=
𝑓𝑠
𝑓0
Considerando amostras equiespaçadas
de a amostra r de G é:𝝎 𝟎=2𝝅𝒇 𝟎
com:
5
B

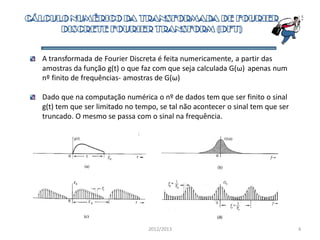
6. A transformada de Fourier Discreta é feita numericamente através da FFT.
O algoritmo da FFT utiliza uma sequência de N amostras do sinal x(t) obtidas
a partir das amostragem do sinal em intervalos Ts .
O resultado desta operação é uma sinal que na frequência corresponde a N
amostras Xd(f) num intervalo de frequência [0,fs] onde fs=1/Ts=2B
representa a frequência de Nyquist.
A resolução na frequência é dada por Δf=fs/N que corresponde à separação
entre amostras.
O algoritmo de cálculo da FFT é computacionalmente mais eficiente se N
corresponder a uma potência de 2.
Quando isso não acontece pode-se transformar N numa potência de 2
através de uma técnica designada por zero-padding.
2012/2013 6