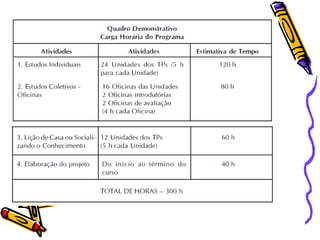
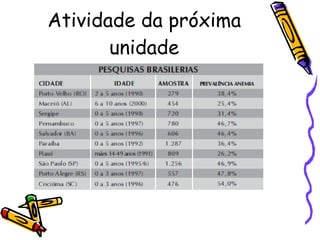
Este documento descreve o programa GESTAR II, um programa de formação continuada para professores com foco no ensino de matemática. O programa utiliza abordagens socioconstrutivistas e contextualizadas para garantir a qualidade do ensino por meio de atividades individuais e coletivas.

1. GESTAR II PROGRAMA GESTÃO DA APRENDIZAGEM ESCOLAR

2. CARACTERIZAÇÃO Formação continuada; Semipresencial; Ensino contextualizado; Concepção sócio-construtivista; Atividades apoiadas em pressupostos* da Educação Matemática. * Pressupostos são hipóteses que precisamos admitir antecipadamente para que possamos aceitar ou compreender as teorias que delas decorrem.

3. Programa Apoiado nos Parâmetros Curriculares Nacionais Números e Operações; Grandezas e Medidas; Espaço e Forma; Tratamento de informação.

4. Objetivo Garantir qualidade no processo de ensino-aprendizagem através de ensino contextualizado, por meio de ações e estratégias de estudo individual e de atividades presenciais, individuais ou coletivas.

5. Proposta Pedagógica Resolução de problemas como forma de construção de conhecimento; Apropriação de conhecimentos; Reflexão e investigação conjunta; Compartilhar experiências; Mobilizar a comunidade;

6. Ações do Gestar Atividades individuais a distância; Oficinas coletivas; Plantão pedagógico; Acompanhamento pedagógico.

7. ORGANIZAÇÃO 120h presenciais 80h – Oficinas 40h – Elaboração do Projeto, plantão e Acompanhamento pedagógico 180h a distância (Total: 300h) Realizada de forma descentralizada

9. Oficinas Serão realizadas nas unidades ímpares; Discussão das experiências matemáticas realizadas na seção ( Resolução da situação-problema ) e na seção 2, ( construção do conhecimento matemático em ação ) 110 minutos; Discussão das experiências realizadas a partir das proposta da seção 3 ( Transposição Didática ) 90 minutos; Pensar no trabalho da próxima unidade ( Introdução a Próxima Unidade ) 30 minutos.

10. Desenvolvimento das atividades 75% nos encontros; Socializando o conhecimento; Elaborar relato de sua prática pedagógica que serão entregues junto com as atividades desenvolvidas pelos alunos Projeto; Desenvolver um projeto, de preferência interdisciplinar, para finalizar o programa. Deverá ser implementado em sala de aula.

11. Estrutura do Projeto Temática: Definir um tema contextualizado a realidade da sala; Problemática: Definir uma situação problema; Fundamentação Teórica: Definir os conceitos e as teorias que darão base as ações desenvolvidas; Objetivos: Gerais e Específicos; Metodologia: Definir os passos a seguir e o material utilizado; Cronograma: Definir o cronograma de cada etapa de desenvolvimento; Equipe de trabalho: Definir a área de conhecimento envolvida e os educadores envolvidos e suas atribuições; Avaliação: Definir o processo de avaliação e os instrumentos a serem utilizados.

12. Diferenças em relação a outros programa de formação Organização do currículo em rede; Conhecimento Matemático situação-problema; realidade-cultural; Aplicação em sala de aula; Teoria e prática da Educação Matemática.

13. Competências Esperadas Identificar temas relevantes que envolve a matemática; Resolver as situações-problemas relacionadas ao tema; Desenvolver conteúdos que surgem naturalmente das situações-problemas; Estabelecer conexões entre os conteúdos.

14. Organização dos TPs Conhecimento matemático; Conhecimentos de educação matemática; Transposição didática.

15. TP1: Matemática na Alimentação e nos Impostos. Conceitos básicos para a matemática da 5ª à 8ª série ou 6º ao 9º ano. Unidades 1 e 2: Medidas e decimais, áreas e volumes, razão, proporcionalidade, escalas, tabelas, gráficos e equações, etc. Unidades 3 e 4: Conceitos discutidos mais pausadamente, esmiuçado e desenvolvimento de novos conceitos.

16. Seção 1 Situação problema que mobilize conhecimentos matemáticos já conhecidos ou buscar outro que emerge naturalmente no contexto

17. Seção 2 Construção de conhecimentos matemáticos. Elaborar procedimentos e conceitos matemáticos envolvidos na seção 1.

18. Seção 3 Conhecimentos matemáticos para os alunos

19. Iniciando os Trabalhos!!!

20. Gráficos Fazer o gráfico de barras das notas de uma turma de 30 alunos como mostra a tabela ao lado. Queremos mostrar graficamente o rendimento da turma. 8,0 6,8 8,8 4,2 6,5 7,0 2,4 7,8 5,5 7,5 6,9 6,3 8,0 3,0 7,0 4,0 3,7 9,5 8,5 4,5 9,8 9,8 3,5 7,0 5,5 7,9 7,3 2,0 6,5 6,0

21. Trabalhando o Texto!!! Texto – sessão 1 – pág. 16. Atividade 1: Construir um gráfico de barras que represente a situação do texto. Responder as questões da pág. 19 (questões abaixo). Comparando a quantidade de comida com o peso do animal, responda: Qual animal come mais? Qual animal come menos? Dentre os animais menores, qual come mais? E menos? Dentre os animais maiores, qual come mais? E menos?

22. IMC Sem uso da calculadora, calcular seu Índice de Massa Corporal dada pela fórmula

23. IMC Faça o registro das estratégias consideradas mais interessantes e criativas, escrevendo-as numa folha grande; analisando e discutindo as principais diferenças entre esses procedimentos; Escolha um relator do grupo que apresentará (com ajuda dos demais membros) os procedimentos utilizados e suas curiosidades e diferenças observadas pela sua equipe.

24. IMC Retomando os pequenos grupos, discutir (15 minutos) em cada equipe qual foi a maior dificuldade na resolução entre as muitas atividades propostas na seção 2 do TP1. Socializar as dificuldades no grande grupo (30 minutos), de acordo com os pontos apresentados pelos grupos;

25. EXPERIÊNCIAS REALIZADAS COM ALUNO Estratégias didáticas utilizadas; Conteúdos matemáticos envolvidos Dificuldades de ordem matemática apresentadas pelos alunos Dificuldades de ordem didática, (aqueles pontos que não o deixou satisfeito quanto os resultados) Resultados: produtos tirados da atividade como painéis, seminários, construções etc. Pesar quanto cada um come Calcular a média entre os pesos Construção e análise da tabela Utilizar a fórmula de índice de massa

26. Atividade da próxima unidade

27. Unidade 2 • A dimensão da amostra considerada na pesquisa é de acordo com a dimensão da população real de cada estado. • O estado de Sergipe possui um número de crianças com carência de ferro bem maior do que o estado de Alagoas. • Há um maior índice de carência de ferro em crianças em São Paulo do que em Salvador. • Criciuma possui o maior número de crianças entre 0 e 3 anos de idade com carência de ferro do que as demais regiões consideradas no estudo. • Da amostra considerada, aproximadamente 325 crianças possuem uma alimentação considerada rica em ferro.