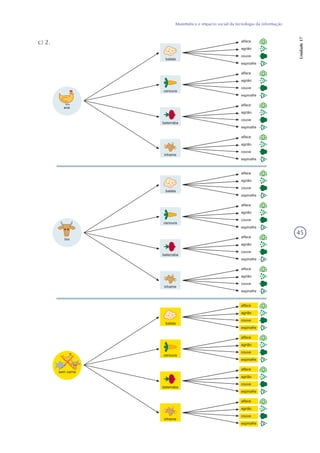
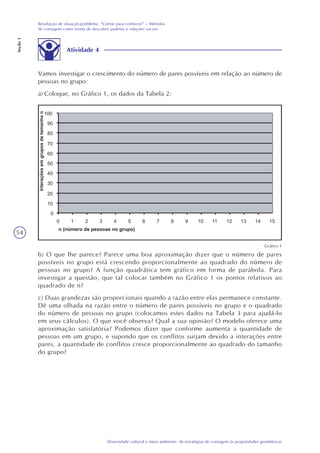
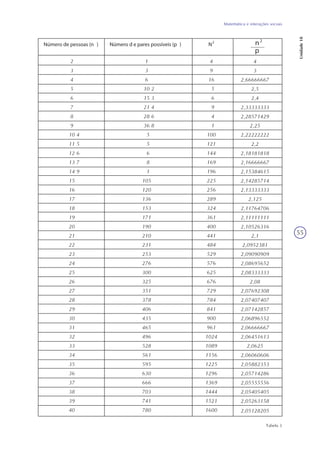
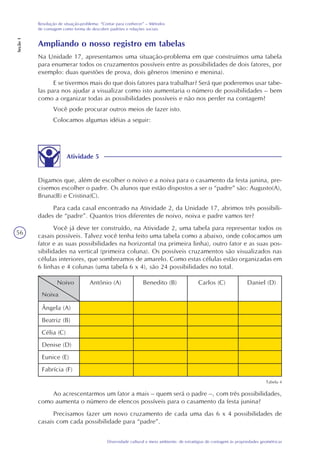
1) A tecnologia da informação, especialmente a internet, tem facilitado vários aspectos da vida moderna, mas também criado novos desafios de segurança;
2) É importante desenvolver habilidades para utilizar a tecnologia de modo adequado, o que pode ser feito em parte nas aulas de matemática;
3) A unidade explora