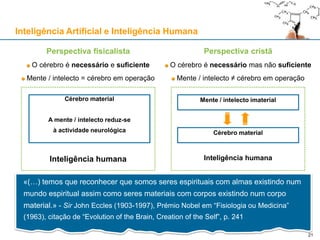
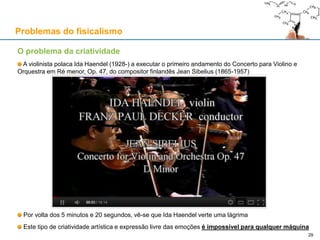
O documento discute a relação entre inteligência artificial e inteligência humana, explorando questões filosóficas como fisicalismo e dualismo. Apresenta diversos argumentos sobre a distinção entre o intelecto humano e as operações computacionais, enfatizando que processos materiais não podem ser reduzidos à compreensão de conceitos abstratos. O texto também questiona a viabilidade do fisicalismo em explicar fenômenos como o livre-arbítrio e a intencionalidade.











![Inteligência Artificial e Inteligência Humana
O teste de Touring e a inteligência artificial
Alan Touring (1912-1954), matemático inglês
“Computing Machinery and Intelligence”, artigo na revista “Mind” (1950)
Touring propõe um teste para detectar comportamento inteligente por parte de
uma máquina: basta que ela se comporte, de certo modo, como um ser humano
Touring quer chegar a um novo conceito de inteligência aplicável a máquinas
No diagrama, o teste está simplificado: C joga contra A ou B e não os distingue
O teste de Touring não estabelece se uma máquina é inteligente, mas sim se
a máquina se comporta, de certo modo, como um ser humano
«Não é difícil imaginar uma máquina que jogará, não muito mal, um jogo
de xadrez. Agora, tomem-se três homens como sujeitos de uma
experiência. A, B e C. A e C são maus jogadores de xadrez e B é o
operador que manuseia a máquina. Duas salas são usadas de forma a
permitir a comunicação [entre elas] dos movimentos [do xadrez], e um
jogo é jogado entre C e, quer A, quer a máquina [através de B]. C pode
achar difícil distinguir contra quem é que está a jogar.» (1948)
20](https://image.slidesharecdn.com/modulox-filosofiadamenteeinteligenciaartificial-130225092107-phpapp02/85/Modulo-X-Filosofia-da-Mente-e-Inteligencia-Artificial-20-320.jpg)







![Consequências dos Teoremas da Incompletude de Kurt Gödel
Para a Matemática…
Destroem o sonho “hilbertiano” de formalizar completamente a Matemática
Para a Física…
Uma vez que qualquer teoria física assenta em modelos matemáticos, criam graves
problemas para a tão procurada “Teoria de Tudo” – será talvez possível formulá-la, mas
nunca demonstrar que tal teoria é a “teoria final”
Para a Mente Humana…
Sustentam o argumento do filósofo John Lucas (1929-) contra a teoria de que a mente
humana é apenas um “software” a correr dentro de um computador biológico (cérebro)
John Lucas, “Minds, Machines and Gödel” (1961):
Lucas diz que os Teoremas da Incompletude de Gödel têm que ser aplicáveis a
programas de computador, pois estes baseiam-se em lógica e aritmética
O argumento de Lucas-Penrose
«podemos produzir modelos [da mente humana] e eles serão iluminadores, mas por muito longe que
cheguemos, ficará sempre mais por dizer – não há limite arbitrário para a pesquisa científica; mas ela
nunca pode esgotar a infinita variedade da mente humana» - John Lucas
34](https://image.slidesharecdn.com/modulox-filosofiadamenteeinteligenciaartificial-130225092107-phpapp02/85/Modulo-X-Filosofia-da-Mente-e-Inteligencia-Artificial-34-320.jpg)

![John Lucas, “Minds, Machines and Gödel” (1961)
Será o intelecto humano algo equivalente a um programa de computador?
Seja H o programa de computador que representaria o intelecto humano em funcionamento…
Então, segundo Gödel, há uma proposição G(H) que H não consegue provar, mas que um
matemático humano (supostamente descrito por H) consegue demonstrar ser verdadeira!
Contradição!
Como é que H não consegue provar G(H), e no entanto consegue prová-la?
Conclusão: por redução ao absurdo…
Como todos os programas de computador são formalizáveis…
… todos os programas de computador estão sob a alçada dos Teoremas de Gödel
Logo, o intelecto humano não pode ser algo equivalente a um programa de computador
O argumento de Lucas-Penrose
«(…) nós não somos máquinas. Podem-se aduzir argumentos para mostrar que as aparências iludem, e
que na verdade somos máquinas, mas argumentos pressupõem racionalidade e, graças ao argumento
godeliano, a única forma sustentável de mecanicismo [fisicalismo] é a de que somos máquinas
inconsistentes; sendo todas as mentes em última análise inconsistentes, então o mecanicismo está
comprometido com a irracionalidade de [qualquer] argumento, e nenhuma sua defesa racional pode ser
sustentada.» - John Lucas
36](https://image.slidesharecdn.com/modulox-filosofiadamenteeinteligenciaartificial-130225092107-phpapp02/85/Modulo-X-Filosofia-da-Mente-e-Inteligencia-Artificial-36-320.jpg)


![Da mente imaterial à alma imortal
Perspectiva hilemórfica acerca da psicologia humana (David Oderberg)
1. Todas as substâncias naturais são compostos de matéria e forma
2. A forma é substancial porque actualiza a matéria e dá identidade e essência à substância
3. A pessoa humana, sendo uma substância, é um composto de matéria e forma substancial
4. A pessoa humana define-se como uma substância individual de natureza racional
5. O exercício da racionalidade é, essencialmente, uma operação imaterial
6. Logo, por 4. e 5., a natureza humana é, ela mesma, imaterial
7. Mas dado que é imaterial, a sua existência não depende de estar unida à matéria
8. Assim, uma pessoa pode existir, graças à sua natureza animal-racional (tradicionalmente
chamada de “alma”), independentemente da existência do seu corpo (perecível)
9. Logo, os seres humanos são imortais, mas a sua identidade e individualidade requer que
estejam unidos a um corpo numa qualquer altura da sua existência
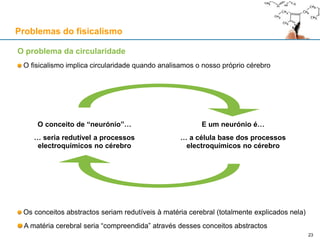
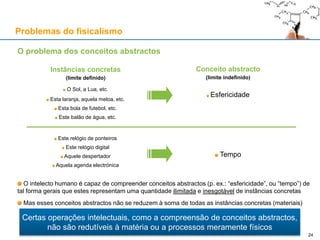
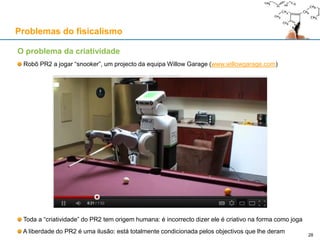
Conclusão
«Eu sigo a clássica definição de Boécio (480-524 d.C.): uma pessoa é definida como uma substância
individual de natureza racional. (…) A forma substancial da pessoa – a sua natureza – é apenas a
animalidade racional da pessoa, sendo “animalidade” o género e “racional” a diferença; [a forma
substancial da pessoa] também é chamada de alma da pessoa.» - David Oderberg
39](https://image.slidesharecdn.com/modulox-filosofiadamenteeinteligenciaartificial-130225092107-phpapp02/85/Modulo-X-Filosofia-da-Mente-e-Inteligencia-Artificial-39-320.jpg)
