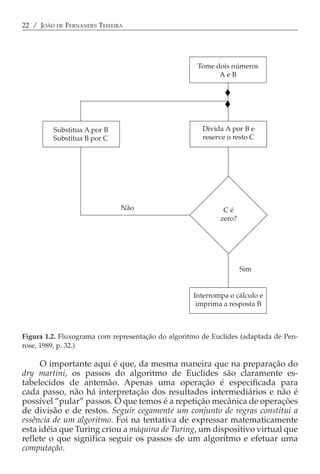
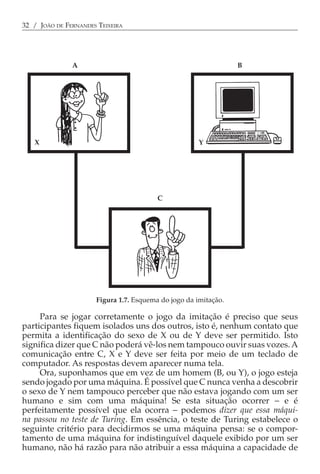
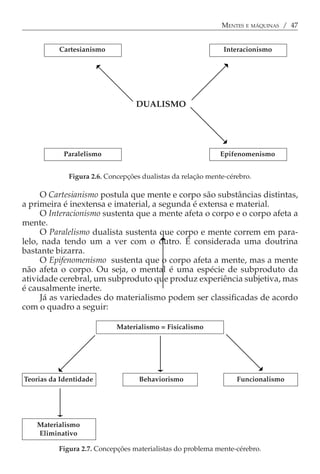
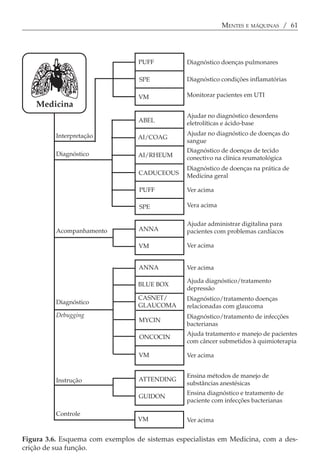
Este documento fornece uma introdução à ciência cognitiva, resumindo: (1) A crise da psicologia no século XX e a necessidade de um novo paradigma; (2) O surgimento da inteligência artificial e como isso levou ao estabelecimento da ciência cognitiva; (3) Os principais modelos propostos, incluindo o funcionalismo e o conexionismo.