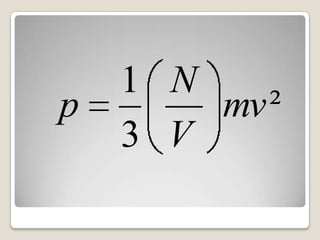O documento descreve o modelo cinético de um gás, explicando que um gás é constituído de partículas (moléculas) em movimento constante devido a colisões elásticas, e que a pressão exercida pelo gás nas paredes do recipiente é resultado das colisões das moléculas. A expressão matemática para a pressão de um gás é derivada usando esse modelo cinético, relacionando a pressão com o número de moléculas, volume, massa e velocidade das moléculas. Essa expressão permite interpretar a

1. Modelo molecular de
um gás
Nomes: Darlei K., Douglas M., Giovane A., Isabel S.,
Viviane D. E.

2. •
Um gás é constituído de partículas ("moléculas")
de volume desprezível e massa m.
•
As moléculas obedecem às leis de Newton e tem
movimento desordenado devido às colisões.
•
As colisões são elásticas, com duração e alcance
desprezíveis.
•
O número de moléculas é muito grande.
Modelo cinético de um gás

3. Numero alto de moléculas;
 Movimento constante;
 A pressão que um gás exerce sobre as
paredes do recipiente que o contém se
deve às incessantes e contínuas colisões
das moléculas do gás contra as paredes
do recipiente;

Cálculo cinético da pressão

4. 




Os físicos do século XIX obtiveram uma
expressão matemática, relacionando a
pressão exercida por um gás com as
seguintes grandezas:
N- número total de moléculas no
recipiente;
V- Volume do recipiente;
m- massa de cada molécula;
v²- média dos quadrados das velocidades
das moléculas;

5. p
1 N
mv ²
3 V

6. Resultado intuitivo;
 Quanto maior o recipiente menos a
pressão exercida pelo gás;
 Quanto maior a massa da molécula maior
a sua quantidade de movimento;
 Quanto maior a média dos quadrados das
velocidades das moléculas maior será a
força que cada molécula exercerá ao
colidir contra a parede do recepiente;

Analisando a expressão
concluímos que :

7. 
A expressão p=(1/3) (N/V) mv² pode ser
escrita assim:
pV
1
Nmv ²
3
Interpretação cinética da
temperatura

8. 
Comparando-a com a equação de um gás
ideal, pV=nRT conclui-se que:
1
Nmv²
3
nRT

9. 
Como N 0 (número de Avogadro) é o
número de moléculas que existe em 1mol
e n, o número de mols que corresponde a
N moléculas, temos:
N
n N0

10. 

Substituindo esse valor de N na igualdade
anterior:
1
n N 0 mv²
3
mv ²
3
nRT
OU
R
N
T
0

11. 
Dividindo se os dois membros dessa
igualdade por 2:
1
mv ²
2
3
2
R
N
T
0

12. O primeiro membro dessa expressão
representa a energia cinética média das
moléculas, representado por C
E
=(1/2)mv²
N 0 ), que aparece no
 O quociente (R/
N
segundo membro é constante pois tanto R
quanto
são constantes. Esse quociente
é representado por K e denominado
constante de Boltzmann.
 Dessa maneira chegamos à seguinte
3
expressão:
EC 2 kT

0

13. 
A temperatura absoluta, T, de um gás está
relacionada cm energia cinética média,
EC
de suas moléculas pela expressão:
3
EC 2 kT
 Em que k é a constante de Boltzmann.

14. Físico Austríaco e professor de
Matemática e Física em várias
universidades da Europa.
 Seu principal trabalho foi o
desenvolvimento da Mecânica Estatística.
 Suas ideias foram fortemente atacadas
por muitos daqueles que não acreditavam
na teoria atômica.

Ludwig Boltzmann (1844-1906)