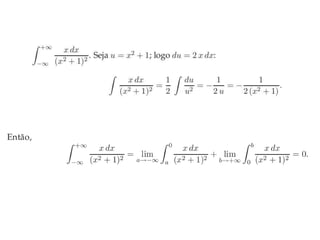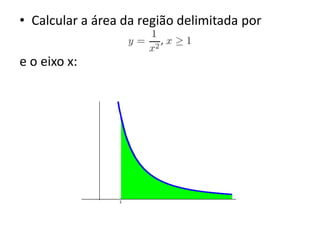
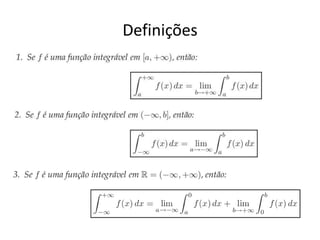
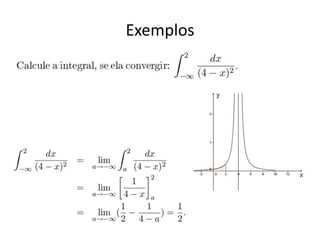
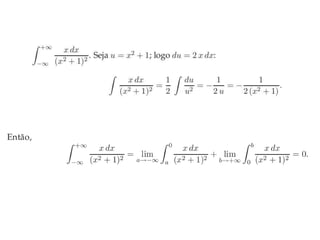
Integrais impróprias estendem a definição de integral definida para funções definidas em intervalos sem limite superior ou inferior ou descontínuas em um ponto. São úteis em diversas áreas como equações diferenciais e estatística. Podem ser convergentes se o limite existir ou divergentes caso contrário.

1. Integrais Impróprias

2. • Na definição de integral definida, consideramos
a função a ser integrada, contínua num intervalo
fechado e limitado. Agora, estenderemos esta
definição para os seguintes casos:
Funções definidas em intervalos do tipo [a,+∞),
(− ∞, b] ou (− ∞,+∞).
A função a ser integrada é descontínua em um
ponto c tal que c ∈ [a, b].

3. • As integrais impróprias são de grande
utilidade em diversos ramos da
Matemática como por exemplo, na
solução de equações diferenciais
ordinárias via transformadas de Laplace e
no estudo das probabilidades, em
Estatística.

4. • Calcular a área da região delimitada por
e o eixo x:

6. Definições

7. • Se nas definições anteriores o limite existir, as
integrais impróprias são ditas convergentes, se
não, divergentes.

8. Exemplos

10. L’Hospital:

12. • Exercícios disponíveis no site.