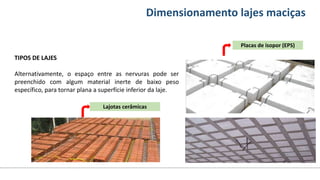
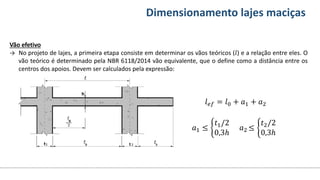
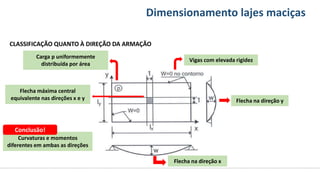
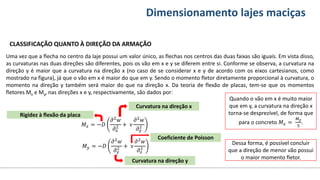
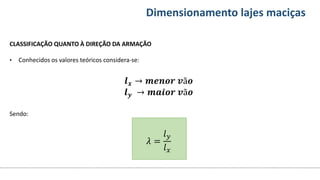
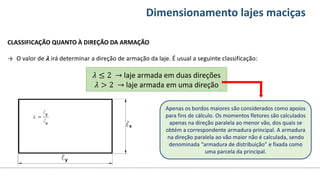
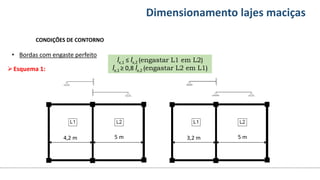
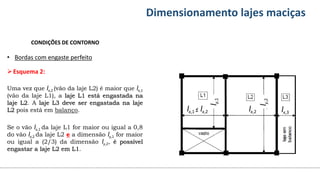
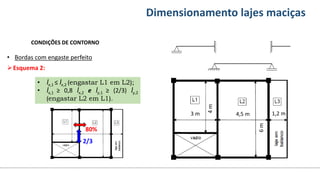
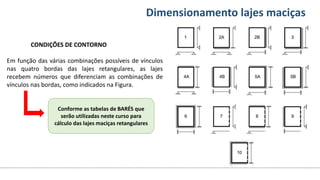
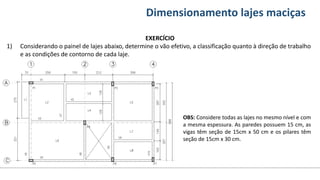
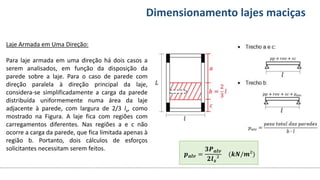
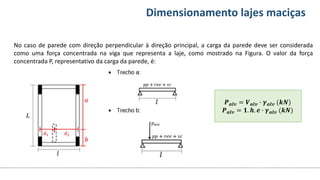
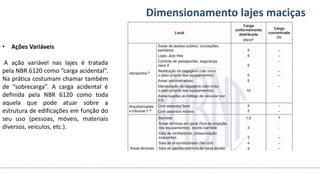
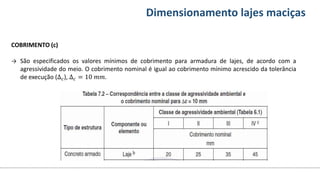
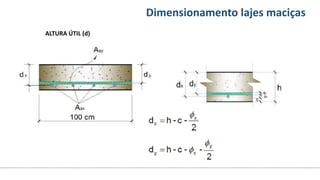
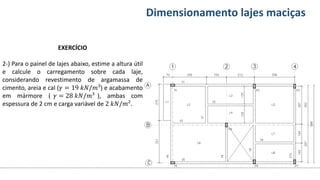
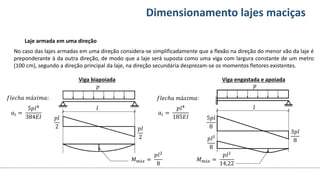
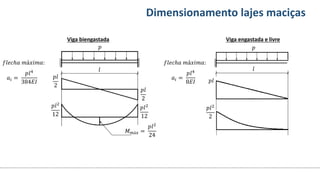
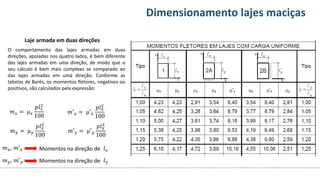
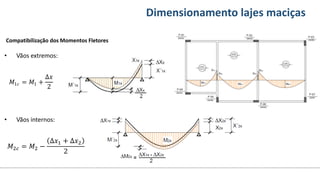
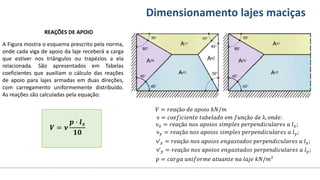
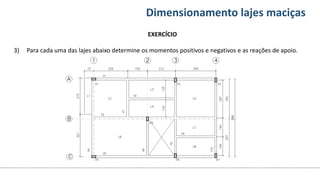
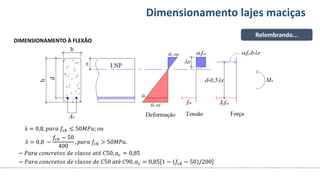
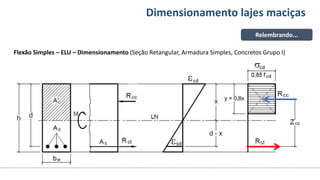
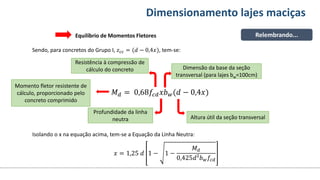
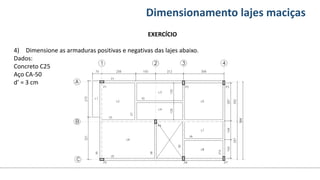
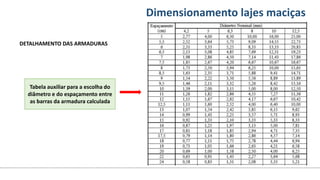
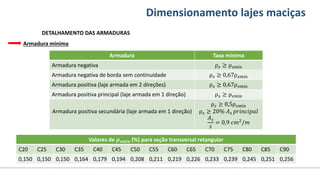
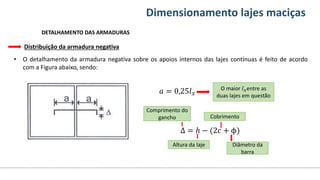
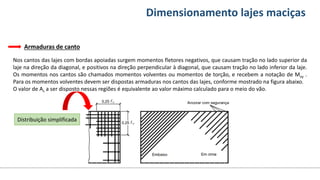
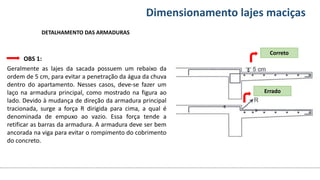
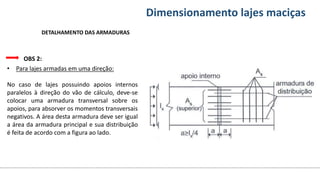
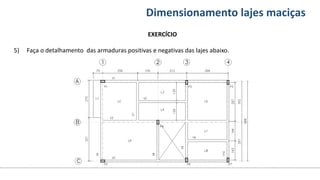
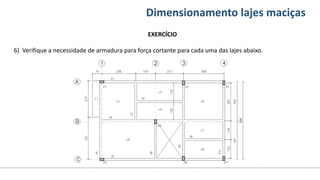
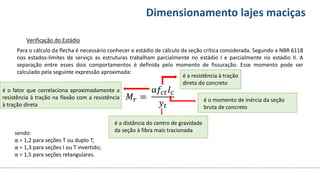
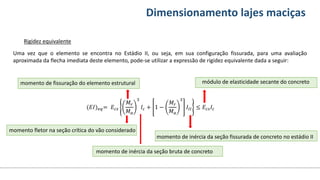
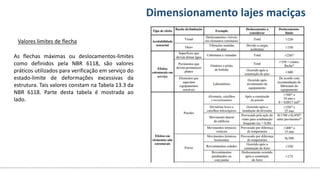
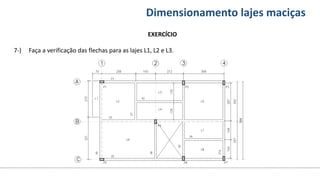
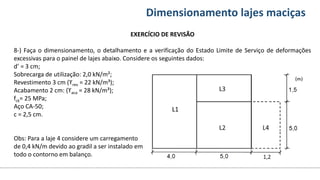
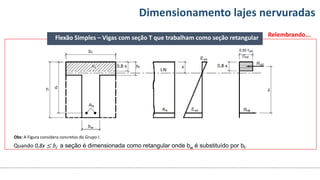
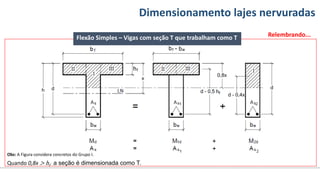
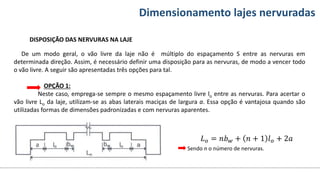
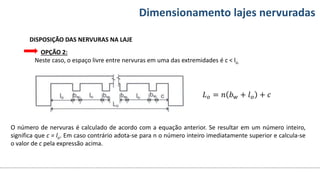
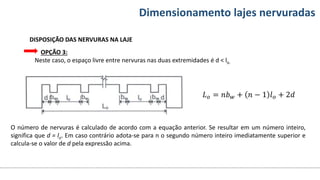
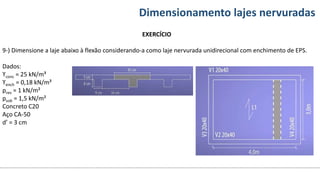
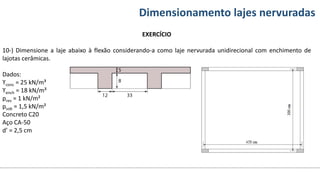
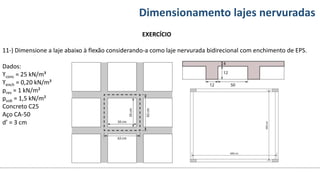
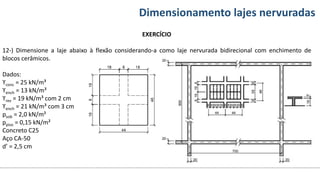
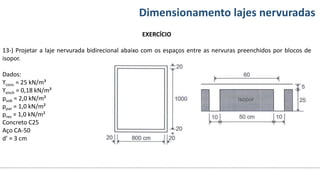
O documento aborda o dimensionamento de lajes maciças no contexto do curso de engenharia civil, descrevendo os tipos de lajes, suas funções, classificações e os princípios de cálculo necessários para garantir a segurança e eficiência estrutural. Detalha considerações como ações aplicadas, espessuras mínimas, e condições de contorno, bem como as especificações de projeto segundo normas técnicas. O conteúdo também inclui exercícios práticos para aplicação dos conceitos teóricos apresentados.