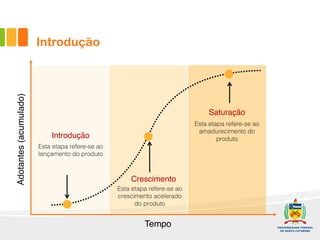
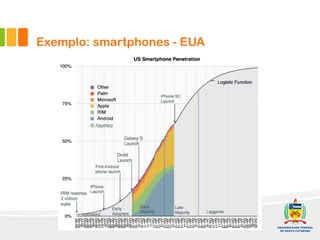
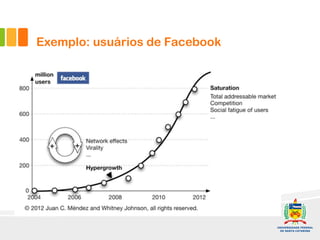
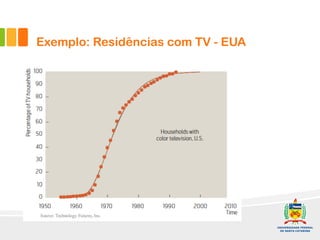
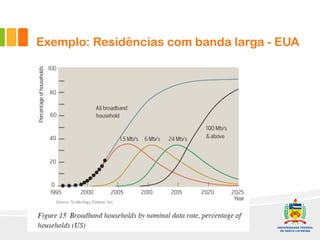
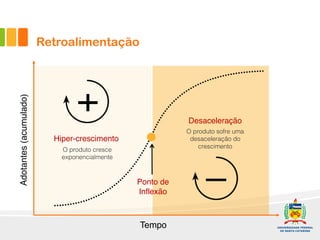
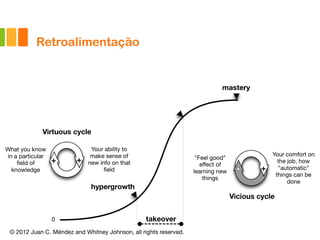
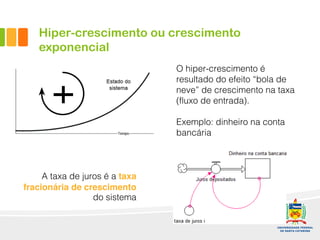
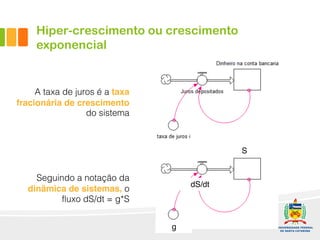
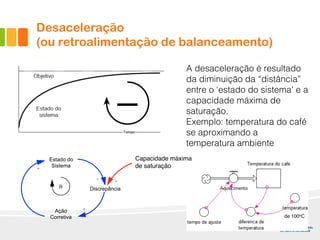
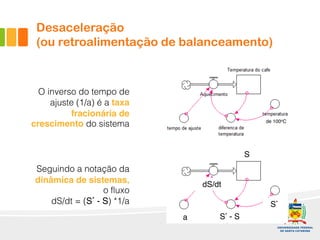
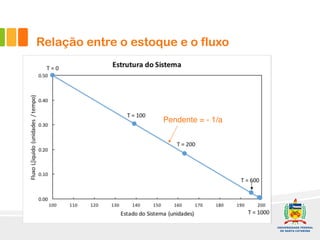
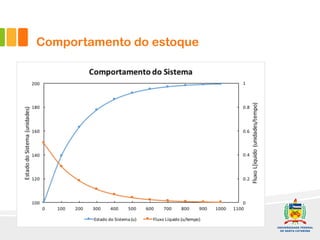
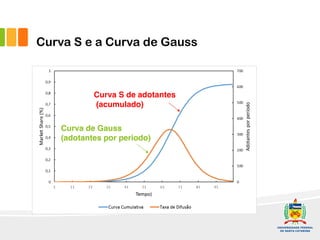
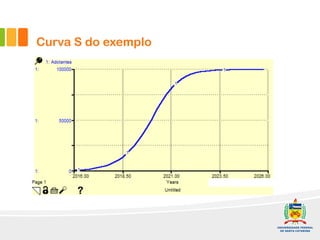
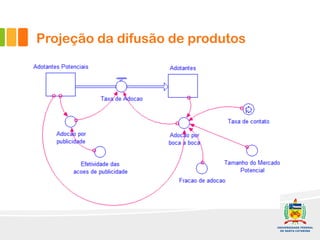
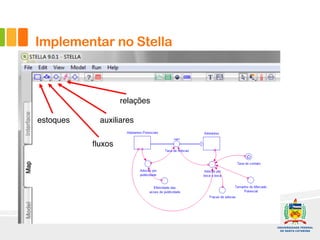
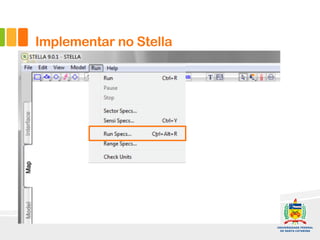
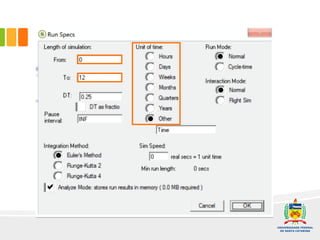
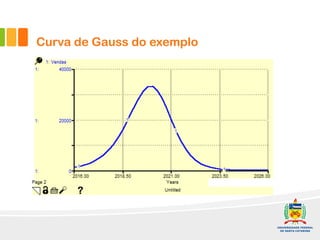
1) O documento discute a difusão de produtos e a forma de crescimento em curva-S. A curva-S é produzida por mecanismos de retroalimentação positiva e negativa que causam hiper-crescimento e desaceleração respectivamente. 2) Um modelo é apresentado para projetar a curva-S com base na adoção por publicidade e efeito boca-boca. Exemplos ilustram como implementar o modelo no software Stella. 3) A bibliografia citada discute a curva-S no contexto de epidem

1. Difusão de produtos e
curva-S
Prof. Dr. Mauricio Uriona Maldonado
EPS 7009 – Teoria da Decisão
Departamento de Engenharia de Produção e Sistemas

2. Introdução
§ A difusão de produtos refere-se ao
comportamento de crescimento de um
determinado produto, desde a entrada no
mercado até a saturação;
§ Os sistemas de apoio a decisão podem ser
utilizados para realizar projeções desse
crescimento, e ajudar na tomada de decisão
sobre investimentos em publicidade e outras.

3. Introdução
§ Estudos prévios comprovam que o formato de
crescimento da difusão de produtos é não-
linear, e segue a forma de uma curva S;
§ A forma de curva S se relaciona com a teoria
do ciclo de vida do produto, que segue uma
trajetória de: introdução do produto,
crescimento e saturação.
https://hbr.org/2017/05/linear-thinking-in-a-nonlinear-world

4. Introdução
Tempo
Adotantes(acumulado)
Saturação
Esta etapa refere-se ao
amadurecimento do
produto
Crescimento
Esta etapa refere-se ao
crescimento acelerado
do produto
Introdução
Esta etapa refere-se ao
lançamento do produto

5. Exemplo: smartphones - EUA

6. Exemplo: usuários de Facebook

7. Exemplo: Residências com TV - EUA

8. Exemplo: Residências com banda larga - EUA

9. Conceito de
retroalimentação

10. Retroalimentação
§ A curva S é produzida por dois mecanismos
de retroalimentação: a retroalimentação de
reforço positivo (hiper-crescimento) e a
retroalimentação de estabilização negativa
(desaceleração);
§ Para compreender melhor o comportamento
da curva S, é necessário compreender o
funcionamenteo de ambos tipos de
retroalimentação.

11. Retroalimentação
Tempo
Adotantes(acumulado)
Desaceleração
O produto sofre uma
desaceleração do
crescimento
Ponto de
Inflexão
Hiper-crescimento
O produto cresce
exponencialmente

12. Retroalimentação

13. Hiper-crescimento ou crescimento
exponencial
O hiper-crescimento é
resultado do efeito “bola de
neve” de crescimento na taxa
(fluxo de entrada).
Exemplo: dinheiro na conta
bancária
A taxa de juros é a taxa
fracionária de crescimento
do sistema

14. Hiper-crescimento ou crescimento
exponencial
A taxa de juros é a taxa
fracionária de crescimento
do sistema
Seguindo a notação da
dinâmica de sistemas, o
fluxo dS/dt = g*S
S
dS/dt
g

15. 𝑑𝑆
𝑆
= 𝑔 ∗ 𝑑𝑡 '
𝑑𝑆
𝑆
= ' 𝑔 ∗ 𝑑𝑡
𝑙𝑛 𝑆 = 𝑔 ∗ 𝑡 + 𝑐𝑆 = 𝑐 ∗ 𝑒.∗/
Curva exponencial
Hiper-crescimento ou crescimento
exponencial

16. T = 600
T = 700
T = 800
T = 900
T = 1000
Pendente = g
Relação entre o estoque e o fluxo

17. Comportamento do estoque

18. A desaceleração é resultado
da diminuição da “distância”
entre o ‘estado do sistema’ e a
capacidade máxima de
saturação.
Exemplo: temperatura do café
se aproximando a
temperatura ambiente
Estado do
Sistema
Ação
Corretiva
Discrepância
-
+
+
Meta ou estado do
sistema desejado
+
B
Desaceleração
(ou retroalimentação de balanceamento)
Capacidade máxima
de saturação
de 100oC

19. Desaceleração
(ou retroalimentação de balanceamento)
O inverso do tempo de
ajuste (1/a) é a taxa
fracionária de
crescimento do sistema
Seguindo a notação da
dinâmica de sistemas,
o fluxo
dS/dt = (S* - S) *1/a
S
dS/dt
a
S*
S* - S
de 100oC

20. Pendente = - 1/a
Relação entre o estoque e o fluxo

21. Comportamento do estoque

22. Curva S e a Curva de Gauss
Curva S de adotantes
(acumulado)
Curva de Gauss
(adotantes por periodo)

23. Modelo para projeção
da curva S

24. 1) O modelo a seguir é utilizado no planejamento de
marketing e vendas para representar o
comportamento das vendas de novos produtos;
2) Oferece uma análise prospectiva muito realista;
3) O modelo representa duas forças de atração (adoção)
de clientes, que funcionam de forma diferente:
i. a força da adoção por ações de publicidade; e
ii. a força da adoção pelo efeito boca-boca (imitação
e interação social).
Projeção da difusão de produtos

25. Projeção da difusão de produtos

26. 1) Quando um novo produto será lançado ao mercado, as
ações de publicidade servem para que os potenciais
clientes desse produto saibam da ‘existência’ desse
novo produto;
2) Ou seja, servem para inicializar o interesse pelo novo
produto e para atrair os compradores ‘menos
conservadores’;
3) No modelo, este efeito é medido por um parâmetro,
denominado ‘efetividade das ações de publicidade’
com valores entre 0-1 (0-100%) que é multiplicado pelo
número total de ‘potenciais adotantes’.
Adoção pelo efeito da publicidade

27. 1) Uma vez inicializada a venda do novo produto,
além do efeito da publicidade entra em jogo um
segundo efeito, o da ‘imitação’;
2) Ou seja, mais e mais potenciais compradores ou
‘adotantes potenciais’ virarão ‘adotantes’ a partir da
compra do produto pelos comentários e avaliações
de outros usuários, por exemplo, de amigos ou
familiares, sobre as qualidades do novo produto;
Adoção pelo efeito boca-boca (1 de 2)

28. 3) Este processo e representado no modelo por uma
variável, denominada ‘adoção por boca a boca’, que
é função de:
§ uma taxa de contato;
§ uma fração de adoção;
§ do tamanho do mercado total de adotantes;
§ do número de adotantes potenciais; e
§ do número de adotantes;
4) Taxa de contato à em número de pessoas
‘contatadas’ por período de tempo;
5) Fração de adoção à parâmetro que mede a
‘infectividade’ de cada contato, com valores entre 0-1
(0-100%).
Adoção pelo efeito boca-boca (2 de 2)

29. Exemplo
§ Vamos assumir que queremos projetar o crescimento
de um produto, no período dos próximos 10 anos (de
2016 a 2026);
§ Sabemos que em 2016, o número acumulado de
adotantes era de 100 clientes;
§ Assumamos que: Fração de adoção * Taxa de Contato =
1,33; e
§ Efetividade das ações de publicidade = 0,011
§ Assumamos também que o tamanho do mercado
potencial é de 100.000 clientes.

30. Adoção por publicidade = Adotantes Potenciais * Efetividade das
ações de publicidade
Adoção por Boca-Boca = Taxa de Contato * Fração de Adoção *
Adotantes Potenciais * (Adotantes / Tamanho do Mercado Potencial)
Taxa de Adoção = Adoção por Publicidade + Adoção por Boca-Boca
Efetividade das ações de publicidade = 0,011
Fração de adoção (0,33) * Taxa de Contato (4) = 1,33
Equações

31. Implementar no Stella
estoques
fluxos
auxiliares
relações

32. Implementar no Stella
fluxos
auxiliares
relações

34. Curva S do exemplo

35. Curva de Gauss do exemplo

36. Bibliografia
1. Sterman, J.D. (2000). Business Dynamics: Systems
Thinnking and Modeling for a complex world. Cap 9.
S-Shaped Growth: Epidemics, innovation diffusion and
the growth of new products.
This work is licensed under a Creative Commons Attribution-
NonCommercial-ShareAlike 4.0 International License.

37. Prof. Dr. Mauricio Uriona Maldonado
EPS 7009 – Teoria da Decisão
Departamento de Engenharia de Produção e Sistemas
Florianópolis, 02/06/17
Difusão de produtos e
curva-S