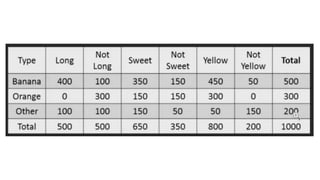
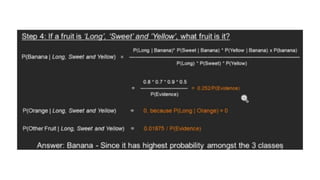
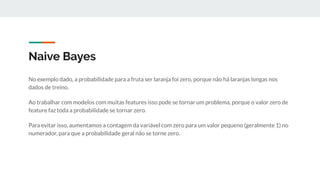
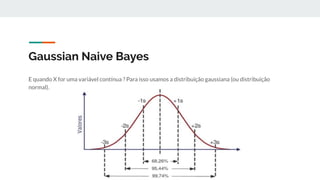
O documento introduz o algoritmo de classificação Naive Bayes, explicando que ele é baseado no Teorema de Bayes e trata cada variável de forma condicionalmente independente. Também apresenta a fórmula matemática do Naive Bayes e demonstra como calcular as probabilidades para classificar novos dados.

1. Introdução a Machine
Learning na prática
Construindo um classificador Naive Bayes

2. Introdução a Machine
Learning na prática
Construindo um classificador Naive Bayes

3. O que é Machine Learn ?

4. Teorema de Bayes

5. O que é Machine Learning ?
Criação de modelos que são aprendidos através de dados.
Usar dados existentes para construir modelos que podem ser usados para prever saídas para novos
dados.

6. Teorema de Bayes
Qual a probabilidade de um evento A ocorrer, dado que um evento B já ocorreu ? P(Professor | Mulher) =
12 / 60 = 0.2.
Homem Mulher Total
Professor 8 12 20
Aluno 32 48 80
Total 40 60 100

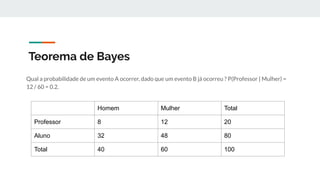
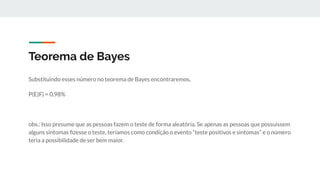
7. Teorema de Bayes
P(E|F) = P(E)/[P(F|E)P(E) + P(F|Ẽ)P(Ẽ)]
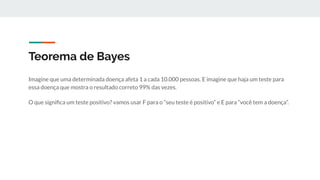
P(F|E), a probabilidade de que alguém com a doença obtenha um resultado positivo, é 0,99.
P(E), a probabilidade de que qualquer pessoa tenha doença é 1/10.000 = 0.0001.
P(F| Ẽ), a probabilidade de que alguém sem a doença obtenha um teste positivo é 0,01.
P(Ẽ), a probabilidade de que qualquer pessoa não tenha a doença é 0,9999.

8. Teorema de Bayes
Substituindo esses número no teorema de Bayes encontraremos,
P(E|F) = 0,98%
obs.: Isso presume que as pessoas fazem o teste de forma aleatória. Se apenas as pessoas que possuíssem
alguns sintomas fizesse o teste, teríamos como condição o evento “teste positivos e sintomas” e o número
teria a possibilidade de ser bem maior.

9. Teorema de Bayes
Imagine que uma determinada doença afeta 1 a cada 10.000 pessoas. E imagine que haja um teste para
essa doença que mostra o resultado correto 99% das vezes.
O que significa um teste positivo? vamos usar F para o “seu teste é positivo” e E para “você tem a doença”.

10. Classificador Naive Bayes

11. Naive Bayes
Algoritmo de machine learn probabilístico;
É baseado no teorema Bayes;
Trata cada variável de forma condicionalmente independentes uma da outra;
Podem ser extremamente rápidos, se comparados a outros métodos mais sofisticados;
Muito usado em processamento de linguagem natural.

12. Fórmula matemática:

13. 

16. Calculando a probabilidade de cada classe
P(Y=Banana) = 500 / 1000 = 0.50
P(Y=Orange) = 300 / 1000 = 0.30
P(Y=Other) = 200 / 1000 = 0.20

17. Calculando a probabilidade de cada feature
P(x1=Long) = 500 / 1000 = 0.50
P(x2=Sweet) = 650 / 1000 = 0.65
P(x3=Yellow) = 800 / 1000 = 0.80

18. Calculando a probabilidade de cada feature,
por classe
P(x1=Long | Y=Banana) = 400 / 500 = 0.80
P(x2=Sweet | Y=Banana) = 350 / 500 = 0.70
P(x3=Yellow | Y=Banana) = 450 / 500 = 0.90

20. Naive Bayes
No exemplo dado, a probabilidade para a fruta ser laranja foi zero, porque não há laranjas longas nos
dados de treino.
Ao trabalhar com modelos com muitas features isso pode se tornar um problema, porque o valor zero de
feature faz toda a probabilidade se tornar zero.
Para evitar isso, aumentamos a contagem da variável com zero para um valor pequeno (geralmente 1) no
numerador, para que a probabilidade geral não se torne zero.

21. Gaussian Naive Bayes
E quando X for uma variável contínua ? Para isso usamos a distribuição gaussiana (ou distribuição
normal).

22. Implementando o classificador
Naive Bayes

23. Introdução a Machine
Learning na prática
Construindo um classificador Naive Bayes