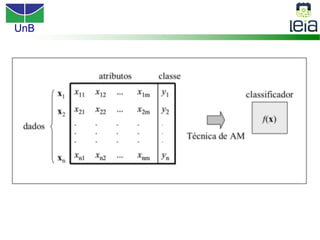
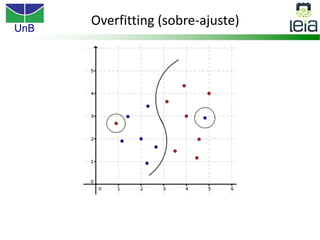
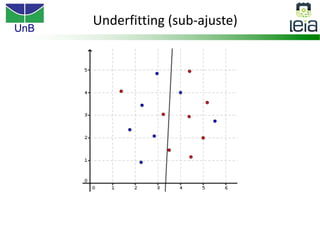
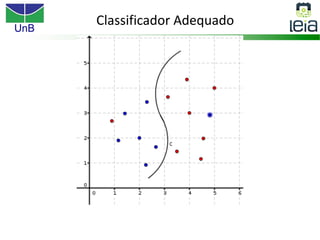
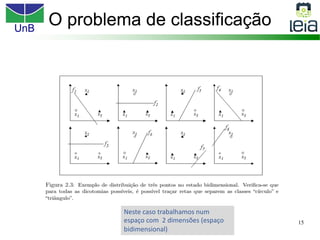
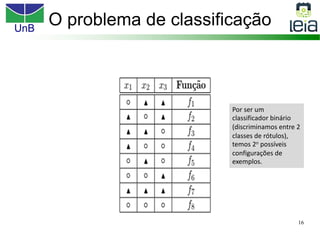
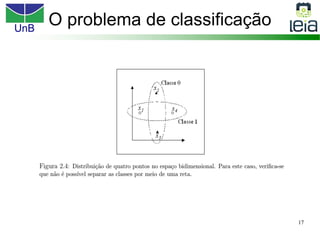
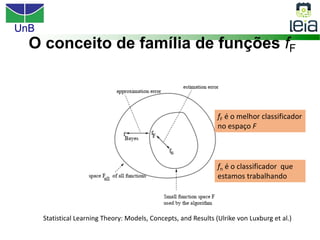
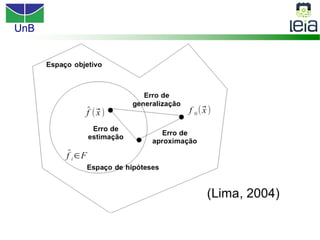
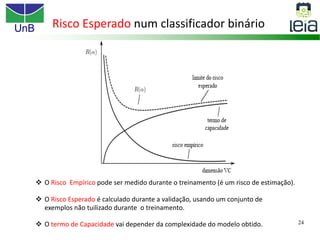
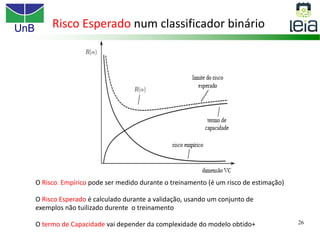
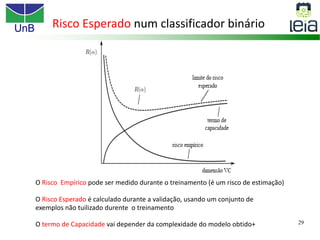
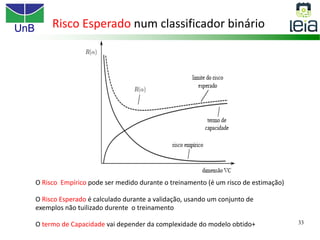
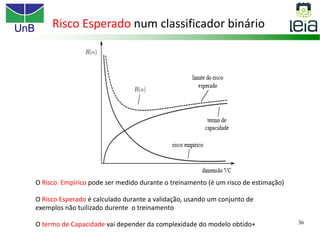
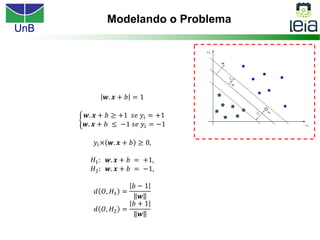
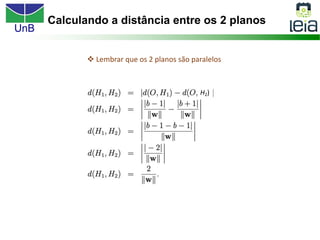
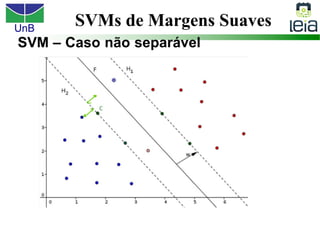
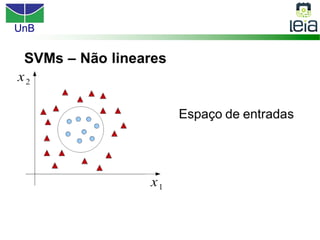
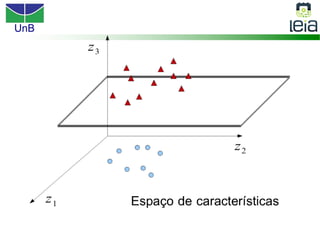
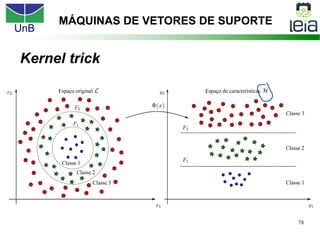
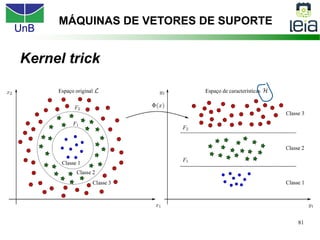
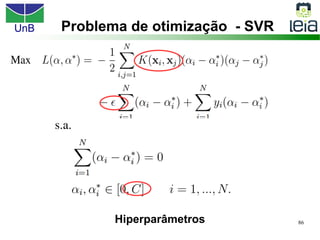
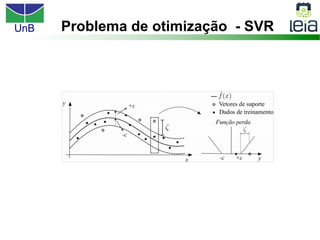
O documento discute sobre máquinas de vetores de suporte (SVMs), apresentando: 1) os tipos de aprendizagem supervisionada, não supervisionada e por reforço; 2) modelos de classificação e regressão para problemas binários e multi-classes; 3) o problema de seleção de parâmetros em SVMs.