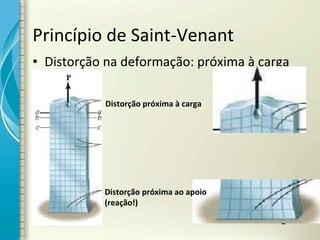
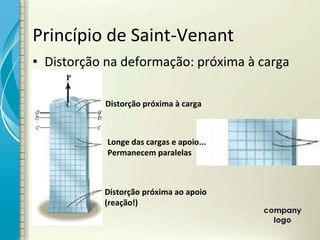
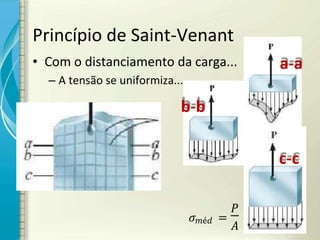
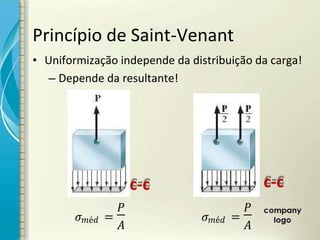
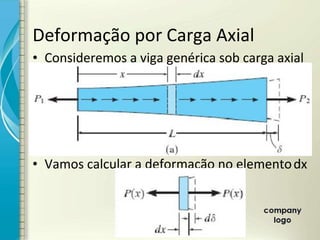
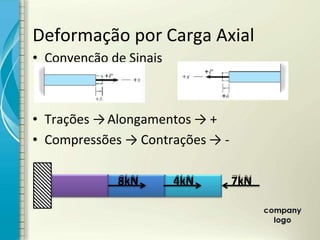
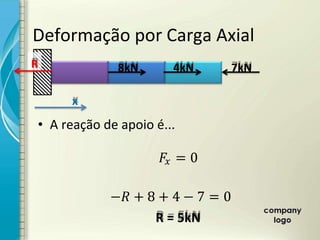
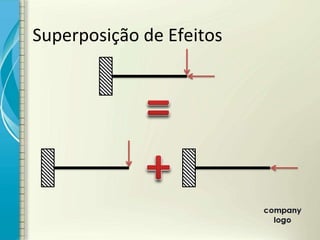
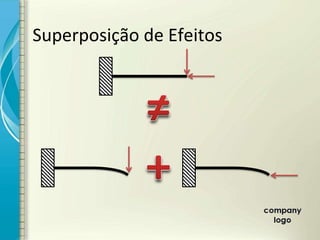
1) O documento discute os princípios de resistência dos materiais, incluindo carga axial, deformação elástica, princípio de Saint-Venant e superposição de efeitos.
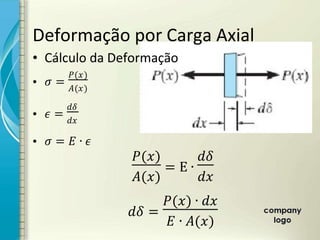
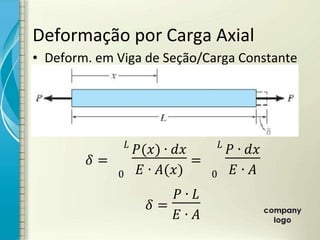
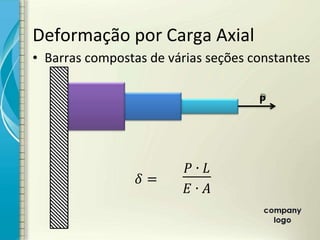
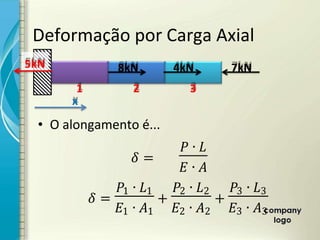
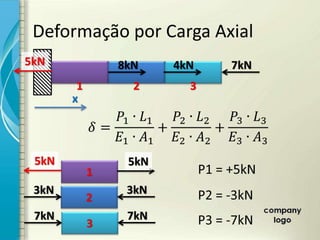
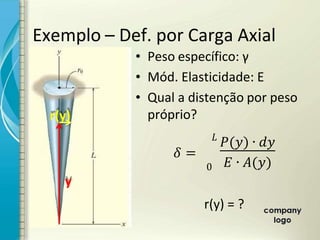
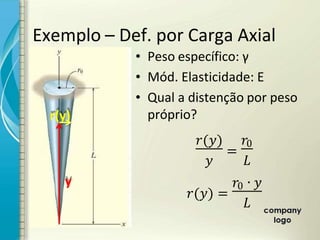
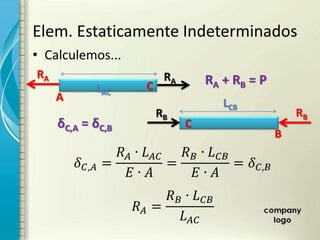
2) É apresentado o cálculo de deformações em elementos sob carga axial constante utilizando o módulo de elasticidade.
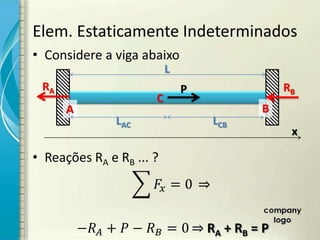
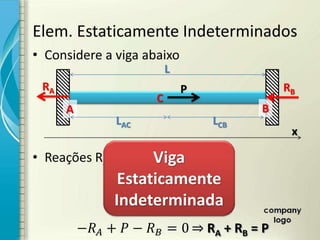
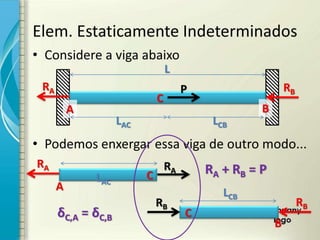
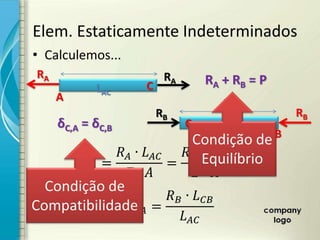
3) Problemas estaticamente indeterminados sob carga axial podem ser resolvidos equacionando a compatibilidade de deformações.