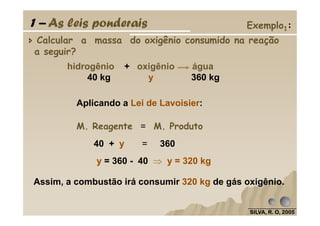
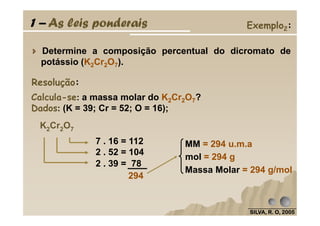
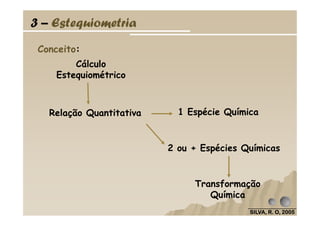
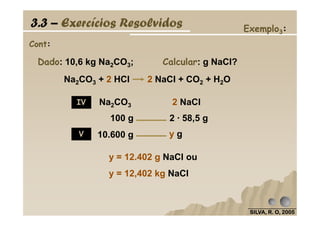
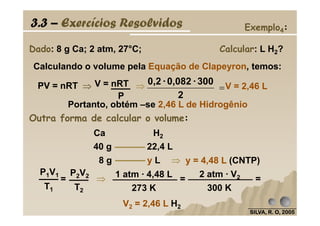
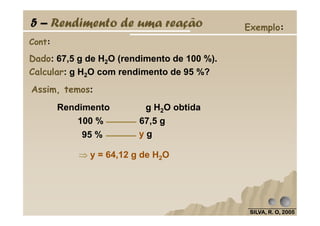
O documento discute as leis fundamentais da química, incluindo a lei de conservação de massa de Lavoisier e a lei das proporções definidas de Proust. Também aborda cálculos estequiométricos, como determinar a composição percentual de compostos e calcular quantidades de reagentes e produtos em uma reação química.