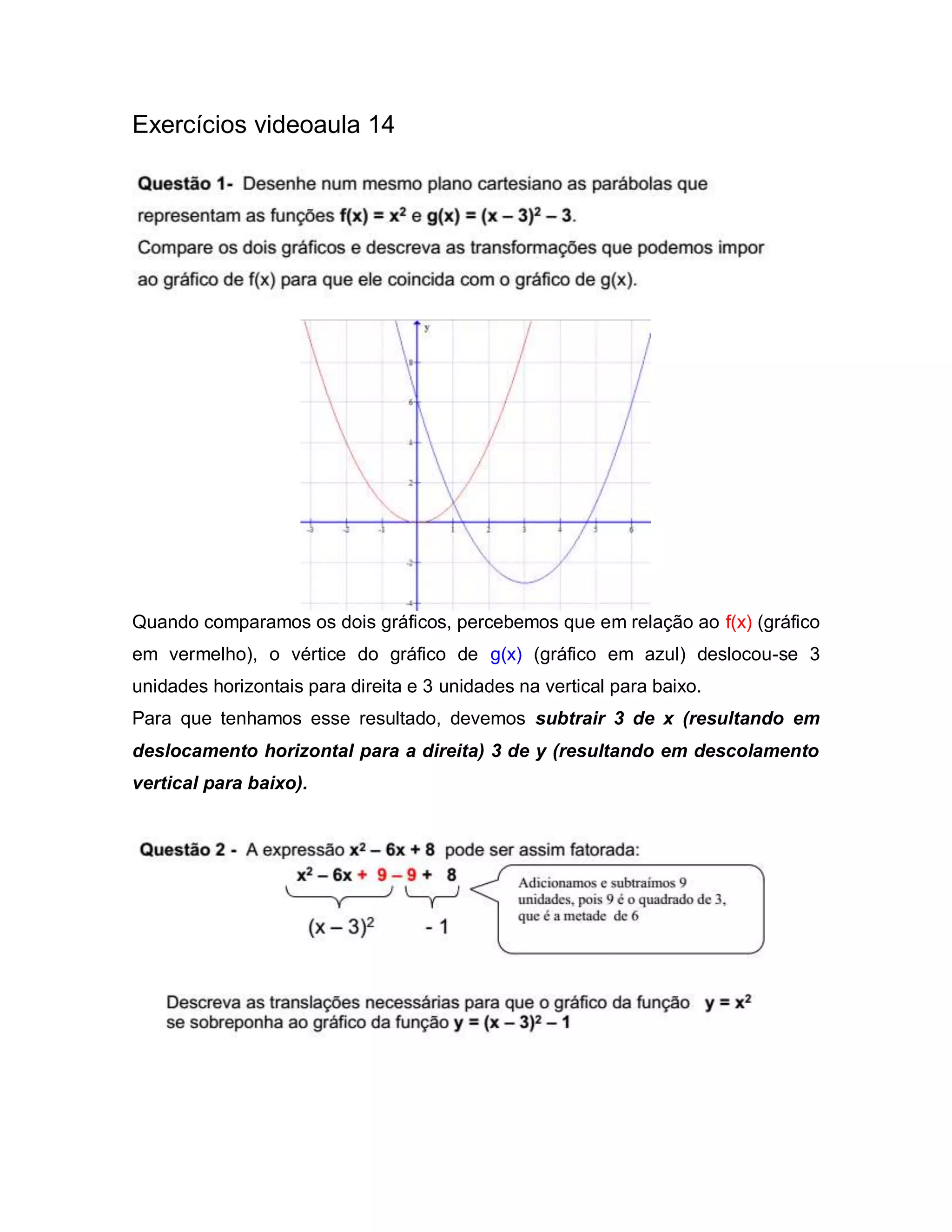
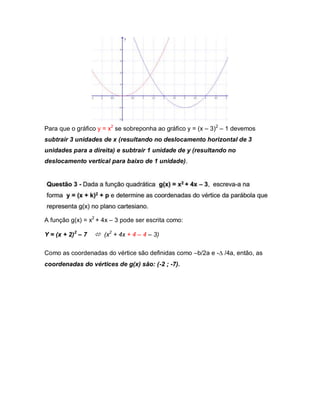
O documento compara dois gráficos de funções quadráticas e explica como transformar uma função em outra através de deslocamentos horizontais e verticais. Ele também mostra como escrever uma função quadrática em outra forma e calcular as coordenadas do vértice.

1. Exercícios videoaula 14
Quando comparamos os dois gráficos, percebemos que em relação ao f(x) (gráfico
em vermelho), o vértice do gráfico de g(x) (gráfico em azul) deslocou-se 3
unidades horizontais para direita e 3 unidades na vertical para baixo.
Para que tenhamos esse resultado, devemos subtrair 3 de x (resultando em
deslocamento horizontal para a direita) 3 de y (resultando em descolamento
vertical para baixo).

2. Para que o gráfico y = x2 se sobreponha ao gráfico y = (x – 3)2 – 1 devemos
subtrair 3 unidades de x (resultando no deslocamento horizontal de 3
unidades para a direita) e subtrair 1 unidade de y (resultando no
deslocamento vertical para baixo de 1 unidade).
A função g(x) = x2 + 4x – 3 pode ser escrita como:
Y = (x + 2)2 – 7  (x2 + 4x + 4 – 4 – 3)
Como as coordenadas do vértice são definidas como –b/2a e - /4a, então, as
coordenadas do vértices de g(x) são: (-2 ; -7).