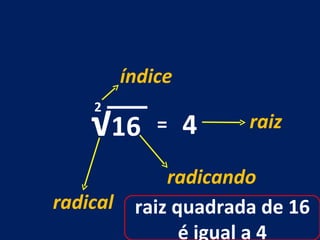
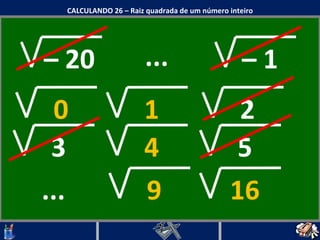
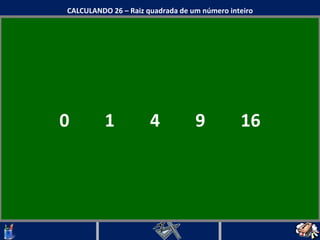
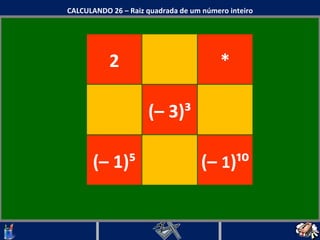
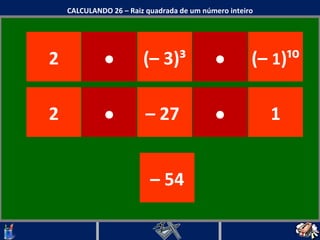
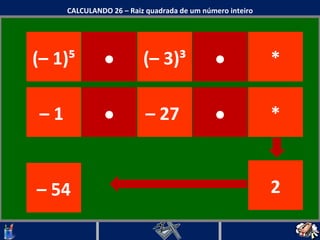
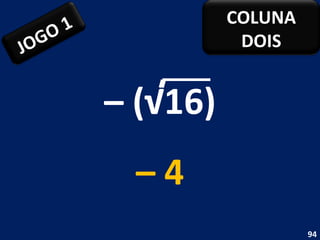
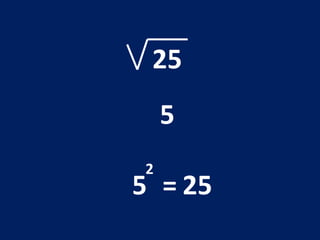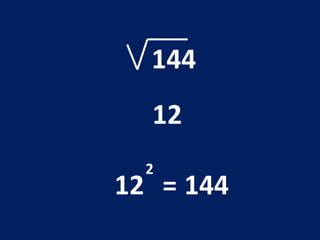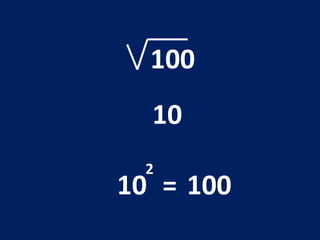O documento discute o conceito de raiz quadrada de números inteiros. Explica que a raiz quadrada de um número inteiro a é um número positivo que, quando elevado ao quadrado, resulta em a. Apresenta exemplos de cálculos de raiz quadrada e esclarece que nem todo número inteiro tem uma raiz quadrada que é um número inteiro.

1. RAIZ QUADRADA DE UM NÚMERO INTEIRO Prof. Materaldo www.matemateens.com.br CEM CENTRO DE ESTUDOS MATEMÁTICOS MAIS DO QUE CÁLCULOS ... AULA 12 7º ANO

2. RAIZ QUADRA DE UM NÚMERO INTEIRO AULA 12

3. O que vimos até aqui?

4. 01 – Sistema de numeração egípcio

5. 02 – Sistema de numeração romano

6. 03 – Sistema de numeração binário

7. 04 – Números inteiros (positivos e negativos)

8. 05 – Adição de números inteiros ( + ) + ( + ) = + ( – ) + ( – ) = – ( + ) + ( – ) = + ou –

9. 06 – Subtração de números inteiros Somar o primeiro com o oposto do segundo

10. ( + ) · ( + ) = ( + ) ( – ) · ( – ) = ( + ) ( + ) · ( – ) = ( – ) ( – ) · ( + ) = ( – ) 07 – Multiplicação de números inteiros

11. 08 – Divisão de números inteiros ( + ) : ( + ) = ( + ) ( – ) : ( – ) = ( + ) ( – ) : ( + ) = ( – ) ( + ) : ( – ) = ( – )

12. 09 – Expressões Numéricas Nas expressões numéricas em que aparecem as operações adição, subtração,multiplicação e divisão devemos efetuá-las nesta ordem: 1º) multiplicações e divisões; 2º) adições algébricas. Sempre na ordem em que aparecem na expressão.

13. 10 – Par ordenado de números inteiros Como um par ordenado indica a localização de determinado ponto, ele também é chamado de coordenadas desse ponto. As retas vermelha e verde são chamadas de eixos.

14. 11 – Potenciação de números inteiros Potenciação é o produto de fatores iguais, obedecendo às regras de sinais da multiplicação. Quando a base é positiva, a potência é sempre positiva Quando a base é negativa e o expoente é par, a potência é positiva. Quando a base é negativa e o expoente é ímpar, a potência é negativa.

15. TUNEL DO TEMPO

16. √ 16 2 = 4 índice raiz radicando radical raiz quadrada de 16 é igual a 4

17. 9 3 3 2 = 9

18. 64 8 8 2 = 64

19. 25 5 5 2 = 25

20. 121 11 11 2 = 121

21. 36 6 6 2 = 36

22. 49 7 7 2 = 49

23. 144 12 12 2 = 144

24. 81 9 9 2 = 81

25. 4 2 2 2 = 4

26. 100 10 10 2 = 100

27. Dados os números naturais a e b tais que b² = a , dizemos que b é raiz quadrada de a , ou seja: √ a = b porque b ² = a

28. Raiz quadrada de um número inteiro A raiz quadrada de um número inteiro a é um número positivo que elevado ao quadrado tem como resultado a .

29. 100 10 ou (– 10) ?

30. Embora haja dois números que elevados ao quadrado resultam 100, (+10) ² = 100 e (– 10) ² = 100, a raiz quadrada de 100 é única: √ 100 = + 10

31. Nem todo número inteiro tem como raiz quadrada um número inteiro.

32. 18 Não existe nenhum número inteiro que elevado ao quadrado resulta em 18

33. 46 Não existe nenhum número inteiro que elevado ao quadrado resulta em 18

34. 8 Não existe nenhum número inteiro que elevado ao quadrado resulta em 18

35. Para que a raiz quadrada de um número inteiro a resulte em um número inteiro, é preciso que a seja um quadrado perfeito.

36. Quadrados perfeitos a 4 9 16 25 36 49 64 81

37. QUADRADO PERFEITO OU NÚMEROS QUADRADOS, são aqueles que são o quadrado, ou segunda potência, de um número positivo.

38. apresenta JORNAL AMAZONÁTICA Um telejornal em defesa do nosso planeta RECOMPENSA ECOLÓGICA

39. ACERTANDO O ALVO - 45 Raiz quadrada de um número inteiro A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br individual

40. 4 2

41. 4 – 2

42. 36 6

43. 36 – 6

44. – 25 Não existe nenhum número inteiro que seja raiz quadrada de – 25

45. 81 – 9

46. 9 3

47. – 9 Não existe nenhum número inteiro que seja raiz quadrada de – 9

48. – 16 Não existe nenhum número inteiro que seja raiz quadrada de – 16

49. 16 – 4

50. 1 – 1

51. 100 10

52. 81 9

53. 64 – 8

54. 49 7

55. 25 – 5

56. 169 13

57. Matema A HISTÓRIA DO NÚMERO UM Parte 5 O Canal de Vídeos da Matemática Tube

58. CALCULANDO 26 Raiz quadrada de um número inteiro A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br duplas

59. Quais são os números compreendidos entre – 20 e 20, cuja raiz quadrada é um número inteiro? CALCULANDO 26 – Raiz quadrada de um número inteiro 1

60. CALCULANDO 26 – Raiz quadrada de um número inteiro ... ... – 20 – 1 0 1 2 3 4 5 9 16

61. 0 1 4 9 16 CALCULANDO 26 – Raiz quadrada de um número inteiro

62. Classifique em V (verdadeiro) ou F (falso). Justifique. A raiz quadrada de 4 é igual a – 2. CALCULANDO 26 – Raiz quadrada de um número inteiro 2

63. FALSO A raiz quadrada de 4 é igual a 2 CALCULANDO 26 – Raiz quadrada de um número inteiro

64. Classifique em V (verdadeiro) ou F (falso). Justifique. A raiz quadrada de um número inteiro é sempre um número inteiro. CALCULANDO 26 – Raiz quadrada de um número inteiro 3

65. FALSO Nem todo número inteiro tem como raiz quadrada um número inteiro. CALCULANDO 26 – Raiz quadrada de um número inteiro

66. Classifique em V (verdadeiro) ou F (falso). Justifique. A raiz quadrada de 25 é igual a + 5 ou – 5, pois (+ 5) ² = (–5)² = 25. CALCULANDO 26 – Raiz quadrada de um número inteiro 4

67. FALSO A raiz quadrada de 25 é igual a 5. CALCULANDO 26 – Raiz quadrada de um número inteiro

68. Cinco cartas estão dispostas no quadro a seguir. Sabendo que os produtos dos números que estão nas diagonais são iguais, determine o número que está no verso da carta de símbolo *. CALCULANDO 26 – Raiz quadrada de um número inteiro 5

69. CALCULANDO 26 – Raiz quadrada de um número inteiro (– 3) ³ (– 1)⁵ * (– 1 )¹⁰ 2

70. CALCULANDO 26 – Raiz quadrada de um número inteiro (– 3) ³ – 54 2 (– 1 )¹⁰ 2 · · · – 27 · 1

71. CALCULANDO 26 – Raiz quadrada de um número inteiro (– 3) ³ – 54 – 1 * (– 1)⁵ · · · – 27 · * 2

72. Observe a potência. (– 4) ͯ. Para qual valor de x a potência é igual a – 64? CALCULANDO 26 – Raiz quadrada de um número inteiro 6

73. Para x = 3 (– 4) ³ = (– 4) · (– 4) · (– 4) = – 64 CALCULANDO 26 – Raiz quadrada de um número inteiro

74. Observe a potência. (– 4) ͯ. Para qual valor de x a potência é igual a + 256? CALCULANDO 26 – Raiz quadrada de um número inteiro 7

75. Para x = 4 (– 4)⁴ = (– 4) · (– 4) · (– 4) · (– 4) = 256 CALCULANDO 26 – Raiz quadrada de um número inteiro

76. Observe e responda. √ n Para qual valor de n a raiz é igual a 8? CALCULANDO 26 – Raiz quadrada de um número inteiro 8

77. Para n = 64 CALCULANDO 26 – Raiz quadrada de um número inteiro

78. Observe e responda. √ n Para qual valor de n a raiz é igual a 20? CALCULANDO 26 – Raiz quadrada de um número inteiro 9

79. Para n = 400 CALCULANDO 26 – Raiz quadrada de um número inteiro

80. Observe e responda. √ n Existe algum valor de n , para que a raiz seja negativa? CALCULANDO 26 – Raiz quadrada de um número inteiro 10

81. Não. A raiz quadrada de n sempre será positiva. CALCULANDO 26 – Raiz quadrada de um número inteiro

82. BOLETEENS Informativo do Clube Matemateens Internet dos carros promete fim da irritação no trânsito

83. Imagine um trânsito onde todos cooperam e ninguém precisa ficar irritado. E, mais do que isso, um trânsito no qual um sistema computadorizado inteligente impede o "efeito manada", virtualmente acabando com os famosos "congestionamentos por excesso de veículos".

84. Engenheiros acreditam que isto não apenas é possível, como já está ao alcance da tecnologia. Tudo o que é necessário fazer é criar a "internet dos carros".

86. Embora não possa controlar diretamente a irritação dos motoristas, a internet dos carros promete um sistema viário projetado a partir de tecnologias cooperativas, permitindo que cada elemento do sistema de trânsito -

87. carros, motoristas, semáforos, placas de sinalização - coopere proativamente para criar um trânsito mais eficiente e mais seguro.

88. Tudo pode começar antes de você pegar o carro pela manhã, com seu celular acordando-o 10 minutos mais cedo porque a chuva está tornando o trânsito mais lento.

89. Indo para o trabalho, antes que você esteja vendo ou ouvindo qualquer sirene, o painel de instrumentos do seu carro começa a emitir um aviso: "Veículo de emergência de passagem no próximo cruzamento!"

90. Você imediatamente tira o pé do acelerador, porque o semáforo à sua frente muda a programação, passa para o amarelo e, em seguida, para o vermelho. O carro de bombeiros passa velozmente porque sabe que encontrará uma sequência de sinais verdes à sua frente até chegar ao local do acidente.

91. Mas você também não fica na mão: antes mesmo que o semáforo passe para o verde, o navegador do seu carro sugere um desvio para evitar a área do acidente, fugindo de qualquer risco de congestionamento.

92. CEM CENTRO DE ESTUDOS MATEMÁTICOS Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br LOTOMÁTICA 76 RAIZ QUADRADA DE NÚMEROS INTEIROS individual

93. CORREÇÃO LOTOMÁTICA 76 RAIZ QUADRADA DE NÚMEROS INTEIROS

94. – (√16) – 4 JOGO 1 COLUNA DOIS

95. √ 16 + √9 4 + 3 7 JOGO 2 COLUNA DO MEIO

96. √ 16 + 9 5 √ 25 JOGO 3 COLUNA DO MEIO

97. √ 36 + 64 10 √ 100 JOGO 4 COLUNA UM

98. √ (– 9) · (– 9) 9 √ 81 JOGO 5 COLUNA DOIS

99. √ 2³ + 1 3 √ 8 + 1 = √9 JOGO 6 COLUNA UM

100. – √ 16 – √9 – 4 – 3 – 7 JOGO 7 COLUNA DO MEIO

101. √ 3³ – 2 5 √ 27 – 2 = √25 JOGO 8 COLUNA DOIS

102. – (√100) – 10 JOGO 9 COLUNA UM

103. (√25 – √49)² (5 – 7)² (– 2)² 4 JOGO 10 COLUNA DOIS

104. – (√16 + √4 ) – (4 + 2) – ( 6 ) – 6 JOGO 11 COLUNA DO MEIO

105. √ 64 · √36 8 · 6 48 JOGO 12 COLUNA UM

106. A nossa diversão é a matemática

107. CRUZADINHA MATEMÁTICA - 01 A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br

108. Horizontal 1 - Polígono de 4 lados 2 – Prefixo que indica três 3 – Medida de tempo Vertical 1 – Unidade de medida de capacidade 2 – Polígono de 5 lados 3 – Ângulo que mede 180º P E N T A G O N O L O S A N G O S L I T R O A N O T R I R A S O 1

109. Horizontal 1 – Número que admite apenas dois divisores 2 – Resultado da adição 3 - Tipo de grandeza que pode ser medida em minuto, hora, dia, etc. Vertical 1 – Resultado da multiplicação 2 – Representação gráfica de uma região, cidade, bairro 3 – Ângulo equivalente a um giro maior do que 0° e menor que 90° P R O D U T O P R I M O M A P T O T A L A G U D O T E M P O 2 A

110. Horizontal 1 – Segunda letra do alfabeto grego 2 – Região plana delimitada por duas semirretas de mesma origem 3 – Um dos termos da multiplicação Vertical 1 – Segmento de reta comum a duas faces de um poliedro 2 – Polígono de 8 lados 3 – Ângulo equivalente a 90° O C T O G O N O A N G U L O B E T A R E T A R E S T A F A T O R 3

111. Horizontal 1 – Unidade de medida de ângulo 2 – Segmento de reta que vai do centro a um ponto qualquer da circunferência 3 – Figura geométrica espacial, cujas faces são quadradas Vertical 1 – Figura geométrica espacial, cujos pontos da superfície estão a uma mesma distância do centro. 2 – Símbolo usado para representar número 3 – Indica quantas partes foram consideradas E A 4 L G A R I S M O C U B R A A U R O N M E R A D O R S F E A

112. AUTO AVALIAÇÃO

113. O DECIMAL - 02 Contando a História da Matemática A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br

114. O DECIMAL Números negativos

115. O DECIMAL Muito tempo se passou até que a noção de número negativo surgisse na história da Matemática.

116. O DECIMAL Povos responsáveis por muitas realizações matemáticas importantes, como egípcios, babilônios e gregos, não trabalharam com esse tipo de número.

117. O DECIMAL Até onde se sabe, os números negativos surgiram inicialmente na China, há pouco mais de dois milênios.

118. O DECIMAL Entre outros fatores, foi a dificuldade de comunicação entre povos distantes que, na época, impediu que essa contribuição dos chineses chegasse logo ao Ocidente.

119. O DECIMAL Na obra mais influente da Matemática chinesa da Antiguidade – Os nove capítulos da arte da Matemática ( século III a.C.) – já se encontram enunciadas as regras de sinais para a adição e a subtração.

120. O DECIMAL Para a subtração, com os mesmos sinais, tire um do outro; tirar positivo do nada dá negativo; tirar negativo do nada dá positivo. Para a adição, com sinais diferentes, tire um do outro; com os mesmos sinais, acrescente um ao outro; positivo com nada dá positivo; negativo com nada dá negativo.

121. O DECIMAL No entanto, não há registro na Matemática chinesa do uso da regra de sinais da multiplicação e da divisão anterior ao século XIII.

122. O DECIMAL Os chineses desenvolveram a prática de operar com números inteiros usando barras de bambu estendidas sobre um tabuleiro.

123. O DECIMAL Para distinguir número positivo de número negativo, adotaram a seguinte convenção: barras vermelhas indicavam números positivos, e barras pretas, números negativos.

124. O DECIMAL Depois dos chineses, acredita-se que os hindus foram o primeiro povo a trabalhar consistentemente com números negativos.

125. O DECIMAL A finalidade inicial era indicar dívidas.

126. O DECIMAL Entre os matemáticos hindus, o primeiro a discorrer sobre os números negativos foi Brahmagupta (século VII), que enunciou até a regra de sinais para a multiplicação.

127. O DECIMAL Os árabes, com o objetivo de disseminar o islamismo (a religião fundada por Maomé, em torno do ano 620), dominaram vários povos, construindo um grande império que se estendia da ...

128. O DECIMAL ... Índia à península Ibérica, passando pelo norte da África. Dessa forma, a soberania sobre os hindus proporcionou-lhes tomar conhecimento das realizações matemáticas desse povo.

129. O DECIMAL Entre elas está o nosso sistema de numeração, criado e desenvolvido na Índia, entre os séculos III e IX.

130. O DECIMAL Como os árabes o difundiram por todo o seu império, ele é chamado sistema de numeração indo-arábico .

131. O DECIMAL A ideia de número negativo também foi absorvida pelos árabes,mas com restrições.

132. O DECIMAL Por exemplo, o grande matemático persa al-Khowarizmi (século IX) não se ocupava de problemas que tinham como resposta números negativos.

133. O DECIMAL Tanto o sistema de numeração indo-arábico como os números negativos não foram aceitos sem resistência no Ocidente.

134. O DECIMAL O sistema de numeração indo-arábico somente se impôs ao sistema romano, apesar de sua notória superioridade , no início do século XVI, embora um tratado de al-Khowarizmi sobre o assunto já tivesse ...

135. O DECIMAL ... sido traduzido para o latim no século XII. Quanto aos números negativos , as dificuldades foram muito maiores.

136. O DECIMAL Essa rejeição é bem ilustrada pelo conteúdo da obra Liber Abaci (“Livro dos Cálculos”, de 1202), a mais importante de Fibonacci (1180-1250), considerado o maior matemático da Idade Média.

137. O DECIMAL O tratado de aritmética, álgebra e geometria – com ênfase no ensino do sistema de numeração indo-arábico – nada incluía sobre números negativos, embora estes já fossem conhecidos pelo autor.

138. O DECIMAL Na verdade, os números negativos foram evitados ou rejeitados pelos matemáticos ocidentais até por volta do século XVII.

139. O DECIMAL Por exemplo, no século XV, o francês N. Chuquet (1450-1500) e, no século XVI, o alemão M. Stifel referiam-se ao números negativos com números absurdos.

140. O DECIMAL O maior matemático francês do século XVI, F. Viète (1540-1630), ignorou-os totalmente em sua obra.

141. O DECIMAL Blaise Pascal (1623-1662), um dos maiores matemáticos de todos os tempos, escreveu em sua obra filosófica Pensamentos :

142. O DECIMAL “ Conhecia pessoas incapazes de entender que quando se tira quatro de zero o que resta é nada”. Fonte: Livro Matemática Realidade – 7º ano – pág. 61 – Atual Editora

143. TV MÁTICA O Canal da Matemática Informação é nosso cálculo apresenta

144. O PODER DO CÉREBRO

145. GRAFICOLÂNDIA - 1 A FUGA DE CHUTEIRAS A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br

146. Jogadores transferidos pela CBF para o exterior Fonte: CBF

147. SUGESTÃO DE LEITURA BIBLIOMÁTICA A BIBLIOTECA DA MATEMÁTICA PARA ENTENDER O MUNDO: OS GRANDES DESAFIOS DE HOJE E DE AMANHÃ de Odile Gandon SÃO PAULO: SM.

148. SIMULÁTICA - 3 O SIMULADO DA MATEMÁTICA AULA 09 – EXPRESSÕES NUMÉRICAS AULA 10 – PAR ORDENADO DE NÚMEROS INTEIROS AULA 11 – POTENCIAÇÃO DE NÚMEROS INTEIROS AULA 12 – RAIZ QUADRADA DE NÚMEROS INTEIROS

149. Uma carta para... ATIVIDADE EXTRA CLASSE

150. www.matemateens.com.br www.twitter.com/matemateens www.youtube.com/materaldo www.twitter.com/materaldo