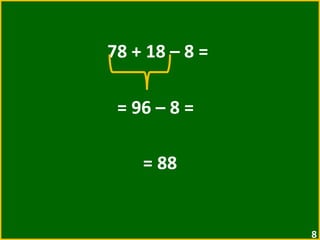
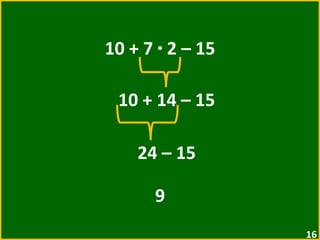
O documento apresenta exemplos de expressões numéricas envolvendo adição, subtração, multiplicação e divisão. Inclui expressões com e sem parênteses, colchetes e chaves. Explica a ordem de operações nesses casos. Por fim, apresenta situações numéricas para serem representadas e resolvidas por meio de expressões.







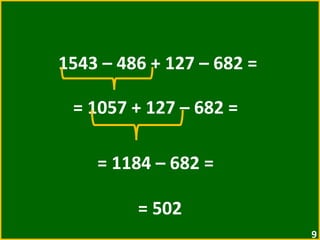
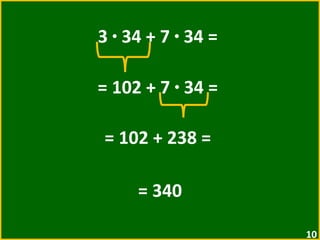
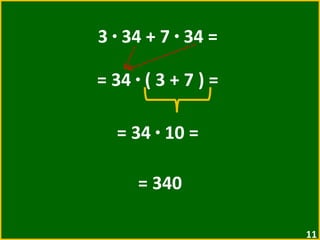
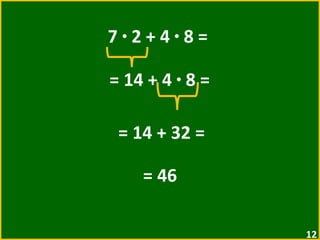
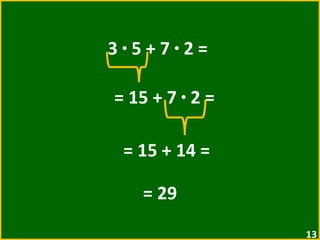
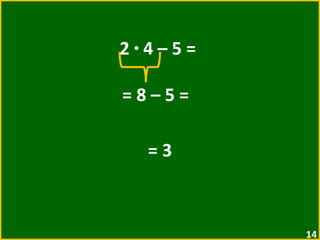
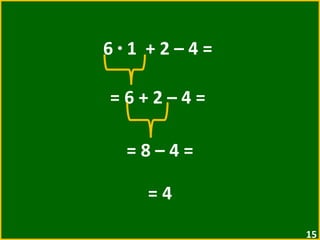



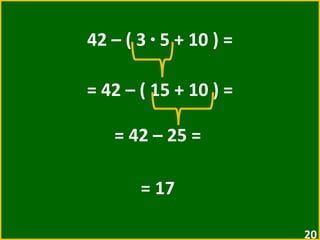
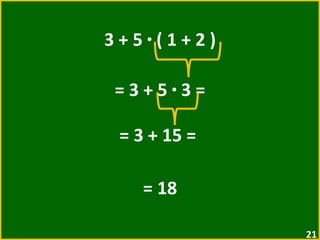
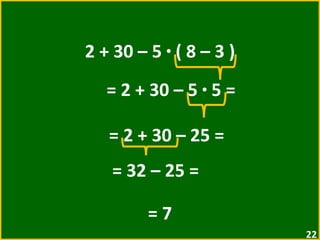
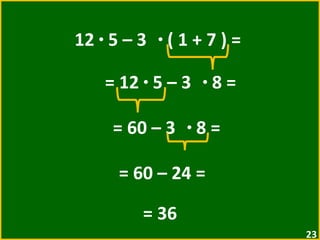
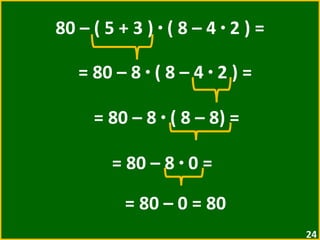




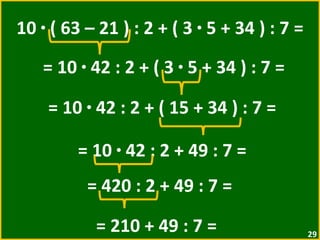
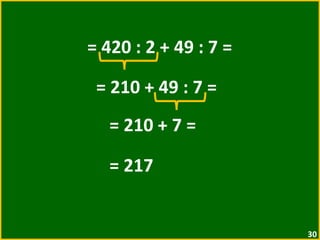
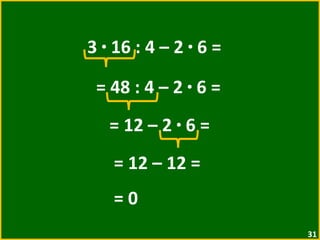


![1º Parênteses ( ) 2º Colchetes [ ] 3º Chaves { }](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-34-320.jpg)


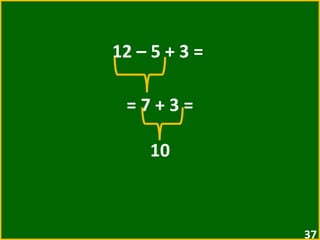
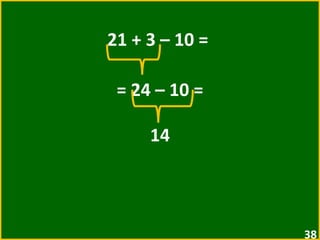
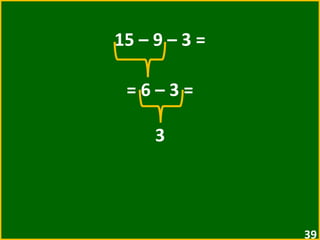
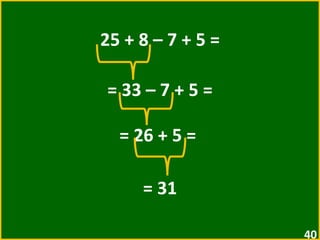
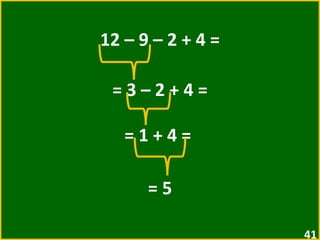
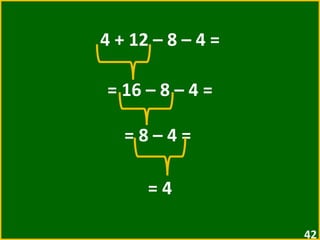

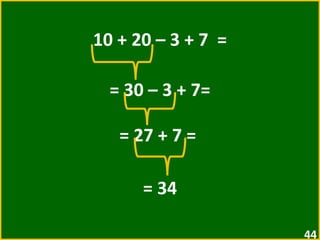
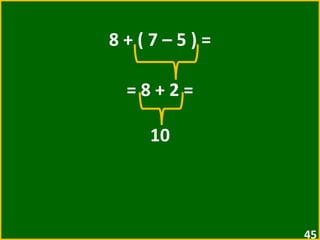
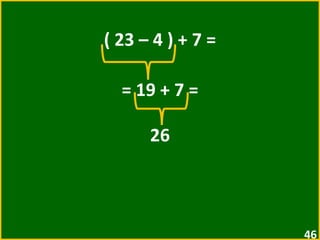
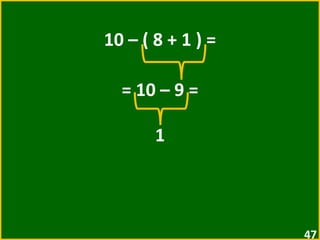
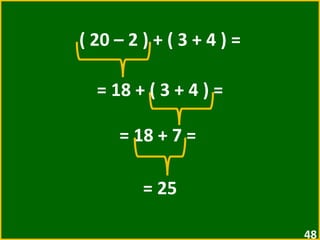
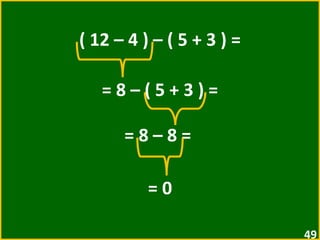
![2 + [ 5 + ( 3 – 1 ) ] = = 2 + [ 5 + 2 ] = = 2 + 7 = = 9](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-50-320.jpg)
![7 – [ 5 – ( 4 + 1 ) ] = = 7 – [ 5 – 5 ] = = 7 – 0 = = 7](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-51-320.jpg)
![10 + [ 13 + ( 2 + 5 ) – 18 ] = = 10 + [ 13 + 7 – 18 ] = = 10 + [ 20 – 18 ] = = 10 + 2 = 12](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-52-320.jpg)
![{ 2 + [ 7 – ( 4 + 2 ) + 1 ] } = = { 2 + [ 7 – 6 + 1 ] } = = { 2 + [ 1 + 1 ] } = = { 2 + 2 } = 4](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-53-320.jpg)
![20 – { 12 + [ 9 – ( 10 – 8 ) ] } = = 20 – { 12 + [ 9 – 2 ] } = = 20 – { 12 + 7 } = = 20 – 19 = 1](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-54-320.jpg)
![100 – { 32 + [ 50 – ( 30 – 15 ) ] – 2 } = = 100 – { 32 + [ 50 – 15 ] – 2 } = = 100 – { 32 + 35 – 2 } = = 100 – { 67 – 2 } = = 100 – 65 = 35](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-55-320.jpg)
![{ 5 + [ 3 + ( 2 + 1 ) ] } – 5 = = { 5 + [ 3 + 3 ] } – 5 = = { 5 + 6 } – 5 = = 11 – 5 = 6](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-56-320.jpg)
![30 – { 18 + [ 7 – ( 3 + 4 ) ] } + 1 = = 30 – { 18 + [ 7 – 7 ] } + 1 = = 30 – { 18 + 0 } + 1 = = 30 – 18 + 1 = = 12 + 1 = 13](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-57-320.jpg)
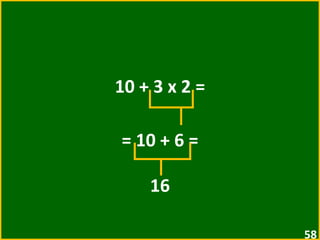
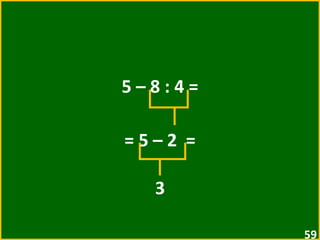
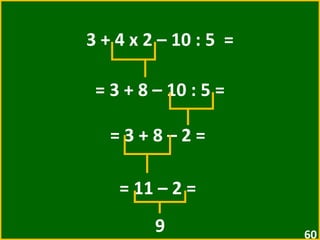

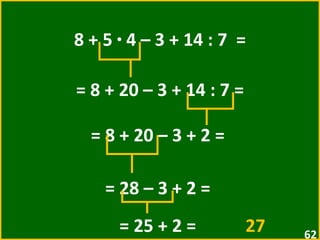
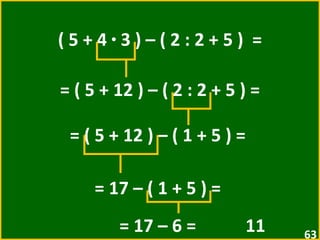
![16 – [ 3 + ( 4 · 2 – 5 ) ] = = 16 – [ 3 + ( 8 – 5 ) ] = = 16 – [ 3 + 3 ] = = 16 – 6 = 10](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-64-320.jpg)
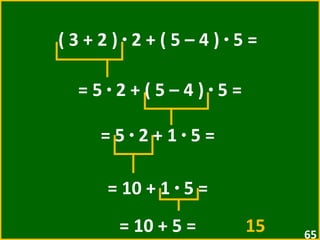
![12 + [ 2 + ( 5 + 3 · 2 ) – 8 ] + 3 = = 12 + [ 2 + ( 5 + 6 ) – 8 ] + 3 = = 12 + [ 2 + 11 – 8 ] + 3 = = 12 + [ 13 – 8 ] + 3 = = 12 + 5 + 3 = 20](https://image.slidesharecdn.com/10-expressesnumricas-100821172233-phpapp01/85/AULA-10-6-ANO-CEM-66-320.jpg)