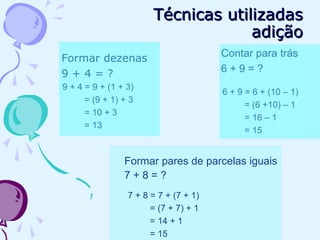
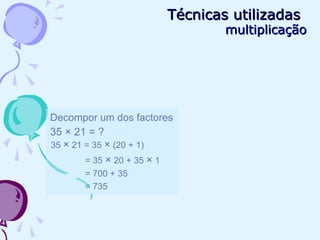
O documento discute estratégias de cálculo mental, incluindo adição, subtração, multiplicação e divisão. Vários exemplos ilustram como decompor números em partes menores para facilitar os cálculos mentalmente. Além disso, o documento descreve o jogo "Jogo do 24" para praticar cálculos mentais de forma lúdica.

1. Cálculo MentalCálculo Mental
Aplicação dasAplicação das
propriedades daspropriedades das
operações básicasoperações básicas

2. Cálculo mentalCálculo mental
• O cálculo mental deve ser explorado
desde muito cedo. Tem por base a
memorização das tabuadas e a
experiência, mas envolve o
desenvolvimento de estratégias pessoais,
o que leva a uma aquisição progressiva
do sentido do número, isto é, a
desenvolver e aprofundar a perspicácia
sobre as estruturas numéricas.

3. - é um pré-requisito para o sucesso do desenvolvimento
de todos os algoritmos escritos;
- promove uma grande compreensão da estrutura dos
números e das suas propriedades;
- promove o pensamento independente e criativo no
manusear dos números;
- contribui para um melhor desenvolvimento da
habilidade na resolução de problemas e;
- é a base para o desenvolvimento da habilidade do
cálculo.
Cálculo MentalCálculo Mental

4. Cálculo mental e o ensinoCálculo mental e o ensino
• Plunkett citado por Goméz (1998) afirma
que o tempo dedicado ao cálculo mental é
irrelevante em comparação com o tempo
dedicado ao cálculo escrito.
• Muitas vezes os alunos com boa destreza
no cálculo escrito tendem a calcular
mentalmente utilizando as técnicas dos
algoritmos escritos, o que representa uma
dificuldade acrescida: o formato escrito
exacto é demasiado difícil para fazer
mentalmente.

5. Cálculo mental e o ensinoCálculo mental e o ensino
• Há um número limitado de regras e
estratégias que facilitam a tarefa de
cálculo.
• Muitos professores não têm a
consciência dos processos que aplicam
quando calculam mentalmente e nunca
pararam a organizá-los no papel com a
finalidade de os ensinar aos seus
alunos.

6. Cálculo mental
• estratégias

7. AdiçãoAdição
• 9+4=?
• 6+9=?
• 7+8=?
• 25+38=?
• 42+35=?
• 43+28=?
• 35+49=?

8. Formar dezenas
9 + 4 = ?
9 + 4 = 9 + (1 + 3)
= (9 + 1) + 3
= 10 + 3
= 13
Formar pares de parcelas iguais
7 + 8 = ?
7 + 8 = 7 + (7 + 1)
= (7 + 7) + 1
= 14 + 1
= 15
Contar para trás
6 + 9 = ?
6 + 9 = 6 + (10 – 1)
= (6 +10) – 1
= 16 – 1
= 15
Técnicas utilizadasTécnicas utilizadas
adiçãoadição

9. Técnicas utilizadasTécnicas utilizadas
adiçãoadição
Adicionar da esquerda para a direita
25 + 38 = ?
25 + 38 = (20 + 5) + (30+8)
= (20 + 30) + (5 + 8)
= 50 + 13
= 63
Decompor uma das parcelas
42 + 35 = ?
42 + 35 = 42 + (30 + 5)
= (42 + 30) + 5
= 72 + 5
= 77
Compensar para obter dezena
43 + 28 = ?
43 + 28 = (43 + 7) + (28 - 7)
= 50 + 21
= 71

10. Técnicas utilizadasTécnicas utilizadas
adiçãoadição
Associar para obter múltiplos de 10
6 + 30 + 1+ 4 + 70 = ?
6 + 30 + 1 +4 + 70 = (70 + 30) + (6+4) + 1
= 100 + 10 + 1
= 111
Decompor e associar para obter múltiplos de 10
35 + 49 = ?
35 + 49 = 35 + (45 + 4)
= (35 + 45) + 4
= 80 + 4
= 84

11. SubtracçãoSubtracção
• 47-32=?
• 53-35=?
• 46-23=?
• 45-29=?

12. Técnicas utilizadasTécnicas utilizadas
subtracçãosubtracção
Subtrair da esquerda para a direita
47 – 32 = ?
47 – 32 = (40 – 30) + (7 – 2)
= 10 + 5
= 15
Compensar para igualar as unidades no aditivo e no subtractivo
53 – 35 = ?
53 – 35 = (53 + 2) – (35 + 2)
= (55 – 35) – 2
= 20 – 2
= 18

13. Subtrair por partes
46 – 23 = ?
46 – 23 = (46 – 20) – 3
= 26 – 3
= 23
Compensar para obter dezenas no subtractivo
45 – 29 = ?
45 – 29 = (45 + 1) – (29 + 1)
= 46 – 30
= 16
Técnicas utilizadasTécnicas utilizadas
subtracçãosubtracção

14. Técnicas utilizadasTécnicas utilizadas
multiplicaçãomultiplicação
Produto de múltiplos de 10
60 × 700 = ?
60 × 700 = (6 × 7) × (10 × 100)
= 42 × 1000
= 42 000
Contar para trás
8 × 99 = ?
8 × 99 = 8 × (100 – 1)
= 800 - 8
= 792
Compensar para obter dezena, centena...
5 × 16 = ?
5 × 16 = (10 ÷ 2) × 16
= (16 × 10) ÷ 2
= 160 ÷ 2
= 80

15. Decompor um dos factores
35 × 21 = ?
35 × 21 = 35 × (20 + 1)
= 35 × 20 + 35 × 1
= 700 + 35
= 735
Técnicas utilizadasTécnicas utilizadas
multiplicaçãomultiplicação

16. Técnicas utilizadasTécnicas utilizadas
multiplicaçãomultiplicação
Decompor um dos factores e compensar para obter
dezenas 15 × 48 = ?
15 × 48 = (10 + 5) × 48
= 10 × 48 + 5 × 48
= 480 + (10 × 48) ÷ 2
= 480 + 480 ÷ 2
= 720
Multiplicar por 11 um número de dois
algarismos
25 × 11 = ?
25 × 11 = 2__5 = 275
2 + 5

17. Técnicas utilizadasTécnicas utilizadas
DivisãoDivisão
Procurar o múltiplo de 10 mais próximo
96 ÷ 2 = ?
96 ÷ 2 =
= (100 – 4) ÷ 2
= 100 ÷ 2 – 4 ÷ 2
= 50 – 2
= 48
Decompor em múltiplos de 11
792 ÷ 11 = ?
792 ÷ 11 =
= (770 + 22) ÷ 11
= 770 ÷ 11 + 22 ÷ 11
= 70 + 2
= 72

18. Técnicas utilizadasTécnicas utilizadas
DivisãoDivisão
• Divisão por 0,5; 0,25; 0,2; 0,125; multiplicando
por 2; 4; 5; 8.
24 ÷ 0,25 =
= 24 ÷ ¼
= 24 × 4
= 96
34 ÷ 0,2 =
= 34 ÷ 1/5
= 34 × 5
= 170
16 ÷ 0,125 =
=16 ÷ 1/8
=16 × 8
= 128
15 ÷ 0,5 =
= 15 ÷ ½
= 15 × 2
= 30

19. Jogos de cálculoJogos de cálculo
mentalmental

20. Jogo do 24Jogo do 24
• Objectivo do jogo: Ganhar o
máximo de pontos por ser o
primeiro a chegar ao resultado 24,
utilizando os 4 algarismos da carta.

21. Jogo do 24Jogo do 24
• As cartas que constituem o jogo:
– As cartas do jogo têm duas faces, cada uma
com diferentes combinações de 4 algarismos.
Nos cantos encontra-se o valor da carta: 1
ponto (1 bola branca), 2 pontos (2 bolas
vermelhas) ou 3 pontos (3 bolas amarelas).
Este valor da carta representa também o seu
nível de dificuldade.
– O algarismo 9 está preenchido a vermelho,
distinguindo-se, assim, do algarismo 6.

22. Jogo do 24Jogo do 24
• Como se joga?
1. À volta de uma mesa colocam-se 4
jogadores, havendo uma quinta pessoa que
será o coordenador da mesa.
2. O coordenador é quem coloca as cartas em
jogo e contabiliza os pontos dos jogadores.
3. O coordenador mantém as cartas consigo e
vai lançando do baralho uma carta de cada
vez, colocando-a no centro da mesa.
4. Pode-se adicionar, subtrair, multiplicar e
dividir. Devem-se utilizar todos os 4
algarismos mas cada um apenas uma vez.

23. Jogo do 24Jogo do 24
5. Ganha a carta em jogo o jogador que
primeiro toque na carta (com apenas um
dedo) e consiga rapidamente dar a
solução correcta.
6. Esse jogador diz primeiro qual a última
operação que efectuou dentro de 3
segundos (p.ex. 4x6=24) e depois tem
15 segundos para dar a solução completa
(p.ex. 2+2=4; 2x3=6; 4x6=24).
7. O jogador que ganhou a carta fica com
ela e passa-se a jogar a carta seguinte.
8. Quando estiverem jogadas todas as
cartas, o coordenador adiciona os pontos
de cada jogador.
9. O vencedor é aquele que conseguir o
maior número de pontos.

24. Jogo do 24Jogo do 24
REGRAS ESPECIAIS
– - Quando os participantes reclamam em
simultâneo a resolução da carta, ganha
aquele que der a resposta primeiro.
- Quando os jogadores não conseguem
encontrar a solução da carta em jogo,
esta pode ser retirada.
- Os participantes devem manter-se
sentados e em silêncio, para que haja
maior concentração durante o jogo.
- Não é permitido aos participantes o uso
de papel, material de escrita e
calculadora.

25. Jogo do 24Jogo do 24
• É falta quando:
• o participante não responde dentro do tempo
estabelecido;
• a solução dada é incorrecta;
• o participante toca na carta com mais de um dedo.
– Uma vez que seja marcada a falta, a carta que
estava a ser jogada é retirada e volta para o
baralho.
– Com três faltas o participante fica desclassificado
da volta que está a ser jogada.
– Um participante desclassificado mantém os pontos
acumulados até ao momento em que é
desclassificado e pode continuar a jogar as voltas
que se seguem começando de novo sem nenhuma
falta.

26. Jogo do 24Jogo do 24
• Para jogar on-line:
– http://www.sc.didaxis.pt/nm/Jogo_do_24.htm
• Soluções das cartas:
– http://www.reijnhoudt.nl/24game/appendixa.h
l