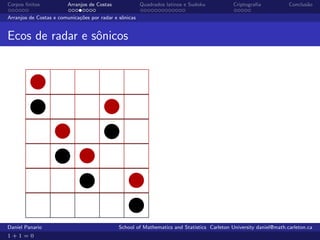
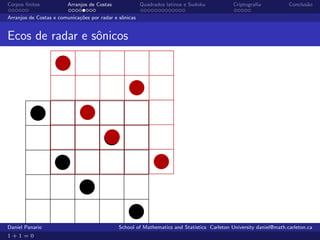
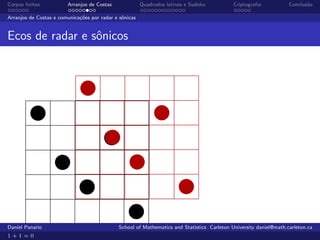
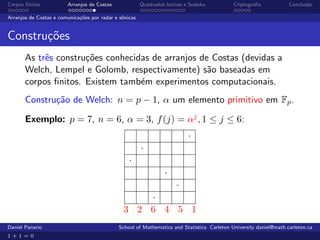
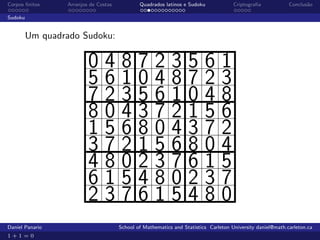
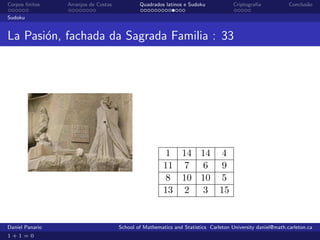
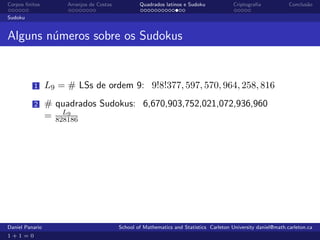
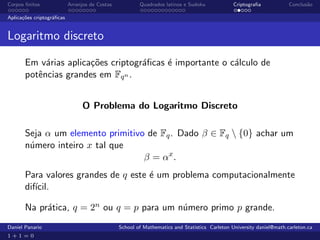
O documento aborda a teoria e aplicações de corpos finitos, enfatizando sua importância em áreas como criptografia, teoria de códigos e comunicações. Ele também discute arranjos de costas, que são usados em comunicações radar e senóricas, além de apresentar a definição e propriedades de grupos e corpos finitos. Exemplos práticos e a história do desenvolvimento desses conceitos são explorados ao longo do texto.