Apontamentos

Alguns Tópicos de Matemática Discreta
Ana Paula Tomás
Departamento de Ciência de Computadores
Faculdade de Ciências do Porto
2005

Conteúdo
1 Conjuntos 1
1.1 Opera¸cões com Conjuntos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2 Representa¸cão de Números em Computador 7
2.1 Sistema de Representa¸cão Posicional . . . . . . . . . . . . . . . . . . . . . . . 8
2.1.1 Rela¸cão entre binário, octal e hexadecimal . . . . . . . . . . . . . . . . 11
2.1.2 Adi¸cão e multiplica¸cão na base b . . . . . . . . . . . . . . . . . . . . . 12
2.1.3 Representa¸cão de números com um número fixo de d´ıgitos . . . . . . . 15
2.1.4 Representa¸cão de números negativos . . . . . . . . . . . . . . . . . . . 16
2.2 Adi¸cão e Subtraçcão em n Bits . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.2.1 Adi¸cão e subtraçcão binária de inteiros não negativos . . . . . . . . . 19
2.2.2 Adi¸cão de inteiros em complemento para 2 . . . . . . . . . . . . . . . 20
2.2.3 Subtraçcão de inteiros em complemento para 2 . . . . . . . . . . . . . 20
2.3 Representa¸cão em V´ırgula Fixa . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.4 Representa¸cão em V´ırgula Flutuante . . . . . . . . . . . . . . . . . . . . . . . 21
3 Algumas No¸cões de Divisibilidade 23
3.1 Bases de Numera¸cão e Critérios de Divisibilidade . . . . . . . . . . . . . . . . 23
3.2 No¸cão de Divisor e de Múltiplo . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.3 Factoriza¸cão em Primos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.3.1 Determina¸cão de primos: crivo de Erastótenes . . . . . . . . . . . . . 27
3.3.2 Cálculo de divisores por análise da factoriza¸cão em primos . . . . . . . 28
3.4 Máximo Divisor Comum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.4.1 Cálculo do máximo divisor comum pelo algoritmo de Euclides . . . . . 29
3.5 M´ınimo Múltiplo Comum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
3.6 Congruências . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
i

4 Indu¸cão Matemática 33
4.1 Princ´ıpio de Indu¸cão Matemática . . . . . . . . . . . . . . . . . . . . . . . . . 33
4.1.1 Erros frequentes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
4.2 Indu¸cão Forte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
4.2.1 Outras formula¸cões do princ´ıpio de indu¸cão . . . . . . . . . . . . . . . 42
5 Rela¸cões Binárias 43
5.1 Rela¸cões Binárias de A em B . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
5.1.1 Opera¸cões com rela¸cões binárias . . . . . . . . . . . . . . . . . . . . . 43
5.1.2 Matriz duma rela¸cão binária . . . . . . . . . . . . . . . . . . . . . . . 45
5.1.3 Fun¸cões de A em B . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
5.2 Rela¸cões Binárias Definidas num Conjunto . . . . . . . . . . . . . . . . . . . . 47
5.2.1 Propriedades das rela¸cões binárias definidas em A . . . . . . . . . . . 48
5.2.2 Grafo da rela¸cão . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
5.3 Rela¸cões de Compatibilidade e de Equivalência . . . . . . . . . . . . . . . . . 50
5.3.1 Classes de equivalência . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
5.3.2 Parti¸cões e rela¸cões de equivalência . . . . . . . . . . . . . . . . . . . . 53
5.3.3 Classes de Compatibilidade . . . . . . . . . . . . . . . . . . . . . . . . 55
5.4 Rela¸cões de Ordem Parcial . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
5.4.1 Diagrama de Hasse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
5.4.2 Máximos, m´ınimos, supremo, ´ınfimo, majorantes e minorantes . . . . 59
5.5 Fechos duma Rela¸cão para uma Propriedade . . . . . . . . . . . . . . . . . . . 60
5.5.1 Fecho transitivo e percursos em grafos . . . . . . . . . . . . . . . . . . 62
5.5.2 Fecho transitivo duma rela¸cão definida num conjunto finito . . . . . . 68
6 Grafos e Multigrafos 71
6.1 Grafos Dirigidos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
6.1.1 Multigrafos dirigidos. . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
6.1.2 Grafos, Percursos e rela¸cões binárias . . . . . . . . . . . . . . . . . . . 74
6.2 Grafos Não Dirigidos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
6.2.1 Grafos Conexos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
6.2.2 Condi¸cão necessária para um grafo ser conexo . . . . . . . . . . . . . . 78
6.3 Árvores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
6.3.1 Árvores com ra´ız . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
6.4 Percursos Eulerianos e Hamiltonianos . . . . . . . . . . . . . . . . . . . . . . 82
6.5 Grafos Planares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
6.6 Isomorfismo de Grafos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
ii

6.7 Colora¸cão de Grafos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
6.8 Grafos com Valores Associados aos Ramos . . . . . . . . . . . . . . . . . . . . 86
6.8.1 Determina¸cão da distância m´ınima . . . . . . . . . . . . . . . . . . . . 87
6.9 Grafos com S´ımbolos Associados aos Ramos . . . . . . . . . . . . . . . . . . . 93
iii

Prefácio
Estes apontamentos têm por base material elaborado em anos anteriores para disciplinas da
licenciatura em Ciência de Computadores [5, 6, 7], o qual foi agora revisto e nalguns tópicos
completado para servir de apoio à disciplina de Matemática para Ciência de Computadores,
no ano lectivo de 2005/06. Não visam substituir a leitura da bibliografia recomendada pelos
docentes e não cobrem actualmente todos os tópicos abordados na disciplina.
v

Cap´ıtulo 1
Conjuntos
Neste cap´ıtulo vamos essencialmente recordar ou introduzir alguma da nota¸cão que é usada
para conjuntos. Tomamos a no¸cão de conjunto como primitiva, convencionando que um
conjunto é constitu´ıdo por elementos – objectos materiais ou entes abstractos que têm
alguma propriedade em comum (no caso extremo, a de pertencerem todos a esse conjunto).
Os conjuntos podem ser vazios (i.e. sem elementos). Em geral, usamos letras maiúsculas
para designar conjuntos e minúsculas para referir os seus elementos. Para indicar que a é um
elemento do conjunto A escrevemos a ∈ A. Os conjuntos podem ser especificados em extensão
– exibindo todos os elementos que os constituem – ou indicando a propriedade que caracteriza
os seus elementos – defini¸cão em compreensão. Por exemplo, {1, 2, 3, 4} e {n | n ∈ Z+∧n ≤ 4}.
Nota¸cão. Sejam A e B conjuntos.
a ∈ A a pertence a A, a é elemento de A
a /∈ A a não pertence a A
A = B igualdade de conjuntos (qualquer que seja x,
x ∈ A se e só se x ∈ B)
A ⊆ B A contido em B, A subconjunto de B
(qualquer que seja x, se x ∈ A então x ∈ B)
A ⊇ B A contém B, B ⊆ A
A ⊂ B A contido propriamente em B,
A subconjunto próprio de B
A ⊆ B ∧ A = B
A ⊃ B A contém propriamente B
A = B A ⊆ B ou B ⊆ A
∅ ou {} conjunto vazio
c A. P. Tomás – Dep. de Ciência de Computadores – FCUP

1.1. OPERAÇ ÕES COM CONJUNTOS 2
O conjunto dos subconjuntos de A, representa-se por P(A) ou 2A. Qualquer con-
junto A pertence ao seu conjunto de subconjuntos, isto é A ∈ P(A). Por exemplo,
P({1, 2, 3}) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
O conjunto P({1, 2, 3}) tem 23 elementos. Também se pode verificar que P(P({1, 2, 3}))
tem 223
elementos. Se A tem n elementos, P(A) tem 2n elementos.
Nestes apontamentos, N representa o conjunto dos inteiros não negativos (incluindo
assim também 0).
N inteiros não negativos (em vez de N0)
Z inteiros
Q racionais
R reais
R+
0 reais não negativos
R+ reais positivos
R− reais negativos
Um conjunto A não vazio é finito se e só se existir uma bijeccão de A em {x ∈ N | x < n}
para algum n ∈ N. Nesse caso, n é o cardinal (número de elementos) de A. Usamos |A| (ou,
alternativamente, #A) para designar o cardinal de A. O cardinal do conjunto vazio é zero.
A propósito de questões de nota¸cão, é de salientar que
{n | n ∈ N}
{n}, com n ∈ N
denotam conjuntos diferentes: o primeiro é N e o segundo é constitu´ıdo por um único inteiro
(que está a ser representado pela letra n).
1.1 Opera¸cões com Conjuntos
A interseçcão de A com B representa-se por A ∩ B, e é o conjunto dos elementos que
pertencem a ambos os conjuntos.
A ∩ B = {x | x ∈ A e x ∈ B}
A união de A com B que se representa por A ∪ B, é o conjunto dos elementos que
pertencem a pelo menos um dos conjuntos.
A ∪ B = {x | x ∈ A ou x ∈ B}

O complementar de B em A representa-se por A B, e é o conjunto dos elementos de
A que não pertencem a B.
A B = {x | x ∈ A e x /∈ B}
Quando está implic´ıto um dado universo U, chama-se complementar de A, e representa-
se por A, ao complementar de A em U, ou seja a U A.
Exemplo 1 Vamos provar que A (B ∪ C) = (A B) ∩ (A C). Para tal vamos mostrar que
x ∈ A (B ∪ C) ⇔ x ∈ (A B) ∩ (A C), qualquer que seja x.
x ∈ A (B ∪ C) ⇔ x ∈ A ∧ x /∈ B ∪ C (por def. de diferen¸ca)
⇔ x ∈ A ∧ (x /∈ B ∧ x /∈ C) (por def. união)
⇔ x ∈ A B ∧ x ∈ A C (por def. de diferen¸ca)
⇔ x ∈ (A B) ∩ (A C) (por def. interseçcão)
Exemplo 2 Quaisquer que sejam os conjuntos A, B ⊆ U, tem-se A ∪ B = A ∩ B. De facto,
se x ∈ A ∪ B então, por defini¸cão de complementar, x /∈ A ∪ B. Logo, x /∈ A e x /∈ B. Mas,
x /∈ A sse x ∈ A. E, x /∈ B sse x ∈ B. Então, x ∈ A e x ∈ B. Donde, x ∈ A∩B. Mostrámos
assim que A ∪ B ⊆ A ∩ B. Reciprocamente,
x ∈ A ∩ B =⇒ (x ∈ A ∧ x ∈ B) (por def. ∩)
=⇒ (x /∈ A ∧ x /∈ B) (por def. complementar)
=⇒ x /∈ (A ∪ B) (por def. ∪)
=⇒ x ∈ A ∪ B (por def. complementar)
ou seja, A ∪ B ⊇ A ∩ B.
Exerc´ıcio 1.1.1 Suponha que os conjuntos indicados são subconjuntos do universo U. Sendo
A, B e C subconjuntos de U quaisquer, mostre cada uma das propriedades:
(a) A B = A ∩ B = B A (j) ∅ = U (r) U = ∅
(b) A B = ∅ sse A ⊆ B (k) A A = ∅ (s) A ∅ = A
(c) A B = A sse A ∩ B = ∅ (l) A = A (t) A ∪ U = U
(d) (A B) ∪ (B A) = (A ∪ B) (B ∩ A) (m) A ∪ A = U (u) A ∩ A = ∅
(e) (A ∩ B) ∩ C = A ∩ (B ∩ C) (n) A ∩ U = A (v) A ∩ A = A
(f) (A ∪ B) ∪ C = A ∪ (B ∪ C) (o) A ∪ ∅ = A
(g) (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)
(h) (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C) (p) A ∪ B = A ∩ B
(i) A (B ∪ C) = (A B) ∩ (A C) (q) A ⊆ B sse B ⊆ A

Exemplo 3 A t´ıtulo de exemplo, vamos analisar a veracidade ou falsidade das afirma¸cões
seguintes e justificá-la.
1. Qualquer que seja x ∈ Z, existe y ∈ Z tal que x ≤ y e x = y.
∀x ∈ Z ∃y ∈ Z (x ≤ y ∧ x = y)
A afirma¸cão é verdadeira porque, sendo o conjunto dos inteiros infinito, se x é inteiro,
x + 1 também é um inteiro e x + 1 é superior a x. Ou seja, dado um x qualquer, se
considerarmos que y é x + 1, satisfazemos a condi¸cão (x ≤ y ∧ x = y). Note que y
dependerá de x.
2. Existe y ∈ Z tal que para todo x ∈ Z se tem x ≤ y.
∃y ∈ Z ∀x ∈ Z x ≤ y
A afirma¸cão é falsa porque em particular se x fosse y+1 então teriamos que ter y+1 ≤ y,
que não é satisfaz´ıvel (já que é equivalente a 1 ≤ 0).
3. Existe um inteiro não negativo que não excede qualquer outro inteiro não
negativo.
∃x ∈ Z+
0 ∀y ∈ Z+
0 x ≤ y
A afirma¸cão é verdadeira. O inteiro 0 é menor ou igual que cada um dos inteiros não
negativos. Aqui, Z+
0 denota o conjunto dos inteiros não negativos, o qual identificámos
também por N.
4. Existe x ∈ Z tal que x é maior do que qualquer outro inteiro y.
∃x ∈ Z ∀y ∈ Z x > y
A afirma¸cão é falsa (análoga à 2).
5. Para todo A ⊆ Z, tem-se P(A) = {∅}.
A afirma¸cão é falsa, porque {1} é um subconjunto de Z e P({1}) = {∅, {1}} = {∅}.
6. Para todo A ⊆ Z, se A = ∅ então P(A) = {∅}.
A afirma¸cão é verdadeira. Só existe um subconjunto de Z que é vazio, e P(∅) = {∅}.
Note que {∅} é um conjunto que tem um elemento. Esse elemento é ∅, ou seja, é o
conjunto vazio.

7. Tem-se P(A) = ∅, para algum A ⊆ Z.
∃A (A ⊆ Z ∧ P(A) = ∅)
A afirma¸cão é falsa, porque qualquer que seja o subconjunto A de Z, o conjunto vazio é
um elemento de P(A).
8. Quaisquer que sejam x, y ∈ Z, tem-se x ≤ y ou y ≤ x.
∀x ∈ Z ∀y ∈ Z (x ≤ y ∨ y ≤ x)
Dizer que x ≤ y equivale a dizer que existe um inteiro não negativo z tal que y = x + z.
É verdade que (x ≤ y ∨ y ≤ x), quaisquer que sejam os inteiros x e y.
Como x − y é inteiro, quaisquer que sejam x e y, se x − y é não negativo, então y ≤ x
pois x = y + (x − y). Se x − y é negativo, então y − x é um inteiro positivo, e como
y = x + (y − x), tem-se x ≤ y.
9. Qualquer que seja A ⊆ Z, se A = {−1, 2, 3} então 4 ∈ A.
∀A ( (A ⊆ Z ∧ A = {−1, 2, 3}) ⇒ 4 ∈ A) )
Falso. Existe um subconjunto de Z que é diferente de {−1, 2, 3} e que não tem o 4. Por
exemplo, o conjunto vazio.
10. Quaisquer que sejam A, B ⊆ Z, se 5 ∈ A B então 5 ∈ A.
∀A ∀B( (A ⊆ Z ∧ B ⊆ Z ∧ 5 ∈ A B) ⇒ 5 ∈ A )
A afirma¸cão é verdadeira. Quaisquer que sejam os subconjuntos A e B de Z, tem-se
5 ∈ A B se e só se 5 ∈ A e 5 /∈ B. Logo, se 5 ∈ A B então 5 ∈ A.
11. Para todo o x ∈ Z, e quaisquer que sejam A, B ⊆ Z, se x ∈ A B então x ∈ A.
A afirma¸cão é verdadeira. A justifica¸cão é semelhante à dada para a afirma¸cão anterior
(claro que é necessário falar em x e não em 5!).
12. Existe x ∈ Z tal que x ∈ A B, quaisquer que sejam A, B ⊆ Z.
Esta afirma¸cão pode ser traduzida pela expressão lógica
∃x (x ∈ Z ∧ ( ∀A ∀B ( (B ⊆ Z ∧ A ⊆ Z) ⇒ x ∈ A B) ))
a qual escrevemos por vezes como
∃x ∈ Z ∀A ⊆ Z ∀B ⊆ Z (x ∈ A B)

que é falsa. Quaisquer que sejam os conjuntos A e B se A = B então AB = ∅. Assim,
se tomarmos, por exemplo, A = B = {1}, os conjuntos A e B são subconjuntos de Z e
não existe qualquer inteiro x tal que x ∈ A B.
13. 2 + 2 = 4 ou
√
2 ∈ Z.
A afirma¸cão é verdadeira porque embora
√
2 /∈ Z, é verdade que 2 + 2 = 4.
14. Se 2 + 2 = 4 então
√
2 ∈ Z.
A afirma¸cão é equivalente a “2 + 2 = 4 ou
√
2 ∈ Z”.
15. Se
√
2 ∈ Z então 2 + 2 = 4.
A afirma¸cão é equivalente a “
√
2 /∈ Z ou 2 + 2 = 4”, e como
√
2 /∈ Z, a afirma¸cão é
verdadeira.
16.
√
2 ∈ Z ou 2 + 2 = 4.
A afirma¸cão é verdadeira porque
√
2 ∈ Z.

Cap´ıtulo 2
Representa¸cão de Números em
Computador
Do mesmo modo que “5692 segundos”, “94 minutos e 52 segundos”, “1 hora, 34 minutos e 52
segundos” são designa¸cões ou representa¸cões diferentes da mesma entidade, também 5692(10),
13074(8) e 1011000111100(2) o são. De facto,
1 34 52(60) ≡ 1h34 52 ≡ 1 × 602
+ 34 × 601
+ 52 × 600
5 6 9 2(10) ≡ 5 × 103
+ 6 × 102
+ 9 × 101
+ 2 × 100
1 3 0 7 4(8) ≡ 1 × 84
+ 3 × 83
+ 0 × 82
+ 7 × 81
+ 4 × 80
1 0 1 1 0 0 0 1 1 1 1 0 0(2) ≡ 1 × 212
+ 0 × 211
+ 1 × 210
+ 1 × 29
+ 0 × 28
+ 0 × 27
+
0 × 26
+ 1 × 25
+ 1 × 24
+ 1 × 23
+ 1 × 22
+ 0 × 21
+ 0 × 20
dizendo-se que 60, 10, 8 e 2 são as bases de numera¸cão, respectivas. Habitualmente, escreve-se
5692 em vez de 5692(10), porque a base mais usual para representa¸cão de inteiros é a base 10,
designada por decimal. As bases 8 e 2 são designadas por octal e binária. Se considerarmos
as potências de 2,
212 211 210 29 28 27 26 25 24 23 22 21 20
4096 2048 1024 512 256 128 64 32 16 8 4 2 1
podemos observar que 5692 = 4096+1596 = 4096+(1024+572) = 4096+1024+(512+60) =
. . . = 4096 + 1024 + 512 + 32 + 16 + 8 + 4 = 1011000111100(2).
Analogamente, se considerarmos as potências de 3,
38 37 36 35 34 33 32 31 30
6561 2187 729 243 81 27 9 3 1

2.1. SISTEMA DE REPRESENTAÇ ÃO POSICIONAL 8
podemos verificar que 5692 = 21210211(3). De facto, 5692 = 2 × 2187 + 1318 = 2 × 2187 +
(1 × 729 + 589) = 2 × 2187 + 1 × 729 + (2 × 243 + 103) = . . . = 2 × 2187 + 1 × 729 + 2 × 243 +
1 × 81 + 2 × 9 + 1 × 3 + 1 = 21210211(3).
2.1 Sistema de Representa¸cão Posicional
Num sistema de numera¸cão de base b usam-se b s´ımbolos diferentes para b d´ıgitos (de 0 a
b − 1). Os números são representados por uma sequência de d´ıgitos.
Os d´ıgitos na base 10 são 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Os d´ıgitos na base 2 são 0 e 1, e
normalmente são designados por bits. Por exemplo,
1011102 = 1 × 25
+ 0 × 24
+ 1 × 23
+ 1 × 22
+ 1 × 21
+ 0 × 20
Se a = rmbm + rm−1bm−1 + . . . + r2b2 + r1b1 + r0b0 com rm = 0 e 0 ≤ ri ≤ b − 1 para
0 ≤ i ≤ m então
a ≡ rm . . . r2r1r0 (b)
é a representa¸cão de a na base b. Os coeficientes r0, r1, r2, . . . rm chamam-se d´ıgitos de repre-
senta¸cão de a na base b, sendo r0 o d´ıgito menos significativo e rm o d´ıgito mais significativo.
A representa¸cão é única, o que é consequência da unicidade do quociente e resto da divisão
inteira.
Proposi¸cão 1 (divisão euclideana de inteiros) Quaisquer que sejam a ∈ Z e b ∈ Z+ existe
um e um só q ∈ Z e um e um só r ∈ Z tal que b = aq + r e 0 ≤ r < b.
A q chama-se quociente e a r resto da divisão inteira de a por b, sendo importante a
condi¸cão 0 ≤ r < b para garantir a unicidade.
Corolário 1.1 Quaisquer que sejam a ∈ Z+ e b ∈ Z+ {1}, existem inteiros únicos r0, r1,
r2, . . . rm tais que a = rmbm + rm−1bm−1 + . . . + r2b2 + r1b1 + r0b0, rm = 0 e 0 ≤ ri ≤ b − 1
para 0 ≤ i ≤ m.
Prova: Sejam a e b inteiros com a > 0 e b > 1. Tem-se ou a < b ou a ≥ b.
Se a < b então a = 0b + a. Portanto, 0 < r0 = a.
Se a ≥ b então, por defini¸cão de divisão inteira, existem q0 e r0 únicos tais que a = bq0 +r0,
com 0 ≤ r0 < b. Se q0 < b, toma-se r1 = q0 e obtem-se a = r1b + r0. Se q0 ≥ b, então o
processo repete-se agora para q0. Ou seja, q0 = bq1 + r1, com 0 ≤ r1 < b. Logo,
a = bq0 + r0 = b(bq1 + r1) + r0 = b2
q1 + br1 + r0

Se q1 < b, toma-se r2 = q0 e obtem-se a = b2r2 +br1 +r0. Se q1 ≥ b, então o processo repete-se
agora para q1, e sucessivamente. O processo termina porque a > q0 > q1 > . . . e qualquer qi
é um inteiro não negativo.
Esta prova indica um algoritmo para determina¸cão da representa¸cão dum inteiro a numa
base b.
Exemplo 4 Tem-se 125(10) = 53 = 1000(5) = 26 + 25 + 24 + 23 + 22 + 20 = 1111101(2) =
175(8) = 7D(16). De facto,
125 5
0 25 5
r0 0 5 5
r1 0 1
r2
r3
125 2
1 62 2
r0 0 31 2
r1 1 15 2
r2 1 7 2
r3 1 3 2
r4 1 1
r5
r6
125 8
5 15 8
r0 7 1
r1
r2
125 16
13 7
r0
r1
No entanto, quando se conhecem potências da base, pode ser mais fácil determinar a
representa¸cão por outro método. Por exemplo, para a base 2,
46(10) = 32(10) + 8(10) + 4(10) + 2(10) = 101110(2)
enquanto se se aplicar o algoritmo dado pela prova anterior teria
46 2
0 23 2
r0 1 11 2
r1 1 5 2
r2 1 2 2
r3 0 1
r4
r5
46(10) = 23 × 2 + 0 = (11 × 2 + 1) × 2 + 0 = ((5 × 2 + 1) × 2 + 1) × 2 + 0
= (((2 × 2 + 1) × 2 + 1) × 2 + 1) × 2 + 0
= ((((2 × 1 + 0) × 2 + 1) × 2 + 1) × 2 + 1) × 2 + 0
= 1 × 25
+ 0 × 24
+ 1 × 23
+ 1 × 22
+ 1 × 21
+ 0 × 20
= 101110(2)

Pode interessar também saber qual a representa¸cão decimal dum inteiro dado
numa base b. Para a obter, bastará aplicar a defini¸cão e efectuar os cálculos na base 10.
101110(2) = 1 × 25
+ 0 × 24
+ 1 × 23
+ 1 × 22
+ 1 × 21
+ 0 × 20
= 32 + 8 + 4 + 2 = 46(10)
101110(3) = 1 × 35
+ 0 × 34
+ 1 × 33
+ 1 × 32
+ 1 × 31
+ 0 × 30
= 162 + 27 + 9 + 3 = 201(10)
Para além da base 2, são bastante usadas em Computa¸cão as bases 8 (octal) e 16 (hexa-
decimal). Os d´ıgitos em octal são 0, 1, 2, 3, 4, 5, 6 e 7. Embora os restos da divisão por 16
sejam 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,. . . , 15, por conven¸cão, os d´ıgitos em hexadecimal
a partir de 10 são representados pelas letras maiúsculas de A a F. Deste modo não haverá
qualquer ambiguidade de representa¸cão (por exemplo, fica claro que o hexadecimal 15 designa
o decimal 1×16+5 e F o decimal 15). Os números representados na base octal são por vezes
indexados por (o), por exemplo 235(o), e os representados na base hexadecimal por (h), por
exemplo F15A(h).
Designa¸cão Base D´ıgitos
Binário 2 0 a 1
Octal 8 (=23) 0 a 7
Hexadecimal 16 (=24) 0 a 9, A, B, C, D, E, F
Decimal 10 0 a 9
Exemplo 5 A sequência 78412 não pode representar nenhum inteiro na base 4 porque 7, 8 e 4
não são d´ıgitos base 4. A sequência 001231 não é representa¸cão numa base de numera¸cão,
no sentido acima definido, porque teria zeros não significativos. A sequência 123100 pode
representar um inteiro em qualquer base b superior a 4.
Exerc´ıcio 2.1.1 Converter para binário: 153(10), 153(6), 153(8), 153(16).
Exerc´ıcio 2.1.2 Converter para hexadecimal: 153(10), 151323(10), 153(8), 1010101111(2) .
Exerc´ıcio 2.1.3 Converter para octal: 1123(4), 151323(10), 153(8), 1010101111(2) .
Exerc´ıcio 2.1.4 Converter para a base 251 e 666 os seguintes números em decimal:
1383, 1498, 1500, 1580, 1640
Exerc´ıcio 2.1.5 Represente x, xn e xn − 1 na base x, para x > 1 e n ∈ N.

2.1.1 Rela¸cão entre binário, octal e hexadecimal
Seja por exemplo, 101011110(2) um binário que se pretende converter para octal. Como foi
visto, o inteiro que esse binário representa é
1 × 28
+ 0 × 27
+ 1 × 26
+ 0 × 25
+ 1 × 24
+ 1 × 23
+ 1 × 22
+ 1 × 2 + 0
ou seja 350. A representa¸cão octal correspondente pode ser obtida agrupando os d´ıgitos
binários 3 a 3: uma vez que 8 = 23 e 82 = 26, tem-se
26
(1×22
+0×2+1×2)+23
(0×22
+1×2+1)+(1×22
+1×2+0) = 82
×5+8×3+6 = 536(2)
Em geral se ak . . . a5a4a3a2a1a0(2), sendo k ≥ 0, representa o inteiro
ak2k
+ . . . + a525
+ a424
+ a323
+ a222
+ a121
+ a020
então a representa¸cão em octal do mesmo inteiro pode ser obtida da forma descrita:
ak2k
+ . . . + 23
(a522
+ a421
+ a320
) + (a222
+ a121
+ a020
) =
ak2k
+ . . . + 8(a522
+ a421
+ a320
) + (a222
+ a121
+ a020
)
Notar que na expressão resultante, qualquer potência de 8 tem por coeficiente
ai+222
+ ai+12 + ai
para algum i, o qual é sempre não negativo e inferior a 8, podendo assim ser d´ıgito da
representa¸cão octal. A cada d´ıgito octal correspondem 3 d´ıgitos em binário. Do mesmo
modo, a cada d´ıgito hexadecimal correspondem 4 d´ıgitos em binário. Assim, para converter
um binário a hexadecimal, agrupam-se os seus d´ıgitos em grupos de 4 (da direita para a
esquerda) correspondendo a cada um desses grupos um d´ıgito hexadecimal. Por exemplo,
101011110(2) ⇒ 1 | 0101 | 1110 ⇒ 1 | 5 | E ⇒ 15E(h)
Para converter um binário a octal procede-se de modo idêntico mas formando grupos de 3.
Por exemplo,
101011110(2) ⇒ 101 | 011 | 110 ⇒ 5 | 3 | 6 ⇒ 536(o)
Inversamente, se se pretender converter de hexadecimal a binário basta associar a cada um
dos d´ıgitos hexadecimal o grupo de 4 d´ıgitos binários correspondente. Por exemplo,
3AC3A(h) ⇒ 0011 | 1010 | 1100 | 0011 | 1010 ⇒
11 | 1010 | 1100 | 0011 | 1010 ⇒ 111010110000111010(2)
Notar a elimina¸cão dos zeros não significativos. O que se acaba de ilustrar é um caso particular
da proposi¸cão seguinte.

Proposi¸cão 2 Se z é um inteiro positivo, a cada d´ıgito (com poss´ıvel excep¸cão do mais signi-
ficativo) da representa¸cão de z na base bn corresponde um grupo de n d´ıgitos na representa¸cão
de z na base b, qualquer que seja n inteiro positivo. Mais concretamente, se
akak−1 . . . atnatn−1 . . . a2na2n−1 . . . anan−1 . . . a1a0
com k ≥ 0 é a representa¸cão na base b de um inteiro positivo z então, a representa¸cão do
mesmo inteiro na base bn é
wtwt−1 . . . w1w0
sendo t+1 o número de blocos de n d´ıgitos da representa¸cão de z na base b (podendo o último
ser completado por zeros não significativos), e wi (i ≤ t) o d´ıgito da base bn que representa o
inteiro a2in−1 . . . ain+1ain(b) (representa¸cão base b a menos de zeros não significativos).
Exemplo 6 Por exemplo, para converter 100313210(4) para a base 16, agrupam-se os d´ıgitos
2 a 2, da direita para a esquerda, pois 16 = 42.
100313210(4) = 01 | 00 | 31 | 32 | 10 = 10DE4(16)
Exerc´ıcio 2.1.6 Repita os exerc´ıcios 2.1.1 a 2.1.3.
Exerc´ıcio 2.1.7 Mostre a proposi¸cão anterior. Comece por mostrar que wtwt−1 . . . w1w0
conforme descrito pode ser representa¸cão base bn de z; use em seguida o facto da representa¸cão
numa base ser única para concluir que wtwt−1 . . . w1w0 é a representa¸cão de z. Mostre depois
que se wtwt−1 . . . w1w0 representa z na base bn, a representa¸cão de z na base b é
akak−1 . . . atnatn−1 . . . a2na2n−1 . . . anan−1 . . . a1a0
2.1.2 Adi¸cão e multiplica¸cão na base b
Recorde como se adicionam dois inteiros representados na base 10, calculando por exemplo
987654 + 73561.
987654
+ 73561
. . . 5
(vai 0)
987654
+ 73561
. . . 15
(vai 1)
987654
+ 73561
. . . 215
(vai 1)
987654
+ 73561
. . . 1215
(vai 1)
987654
+ 73561
. . . 61215
(vai 1)
987654
+ 73561
. . . 061215
(vai 1)
987654
+ 73561
1061215

Algoritmo para Adi¸cão (base 10). Se x e y são inteiros positivos representados na
base 10 por xkxk−1 . . . x1x0 e ymym−1 . . . y1y0 respectivamente então a representa¸cão na
base 10 de x + y, digamos spsp−1 . . . s1s0, pode ser obtida da forma seguinte.
xkxk−1 . . . x1x0
+ ymym−1ym−2 . . . y1y0
. . . s0
Caso x0 + y0 < 10, toma-se s0 = x0 + y0 e repete-se o processo para os d´ıgitos seguintes.
Senão, s0 é tal que x0 + y0 = 1s0, adicionando-se 1 a x1 + y1 repetindo-se o processo (global)
para os d´ıgitos seguintes. Quando k < m (respectivamente m < k) pode-se considerar xi = 0,
i ≥ k (respectivamente yi = 0, i ≥ m). Notar que p = max(k, m) ou p = max(k, m) + 1
sendo neste último caso sp = 1.
Adi¸cão (base 3). 2102(3) + 21(3) = (2 × 33 + 1 × 32 + 0 × 31 + 2 × 30) + (2 × 31 + 1 × 30) =
2 × 33 + 1 × 32 + (0 + 2) × 31 + (2 + 1) × 30 = 2 × 33 + 1 × 32 + (0 + 2) × 31 + (1 × 3 + 0) × 30 =
2 × 33 + 1 × 32 + (0 + 2 + 1) × 31 + 0 × 30 = 2 × 33 + (1 + 1) × 32 + 0 × 31 + 0 × 30 =
2 × 33 + 2 × 32 + 0 × 31 + 0 × 30.
2102(3)
+ 21(3)
. . . 0(3)
(vai 1)
2102(3)
+ 21(3)
. . . 00(3)
(vai 1)
2102(3)
+ 21(3)
. . . 200(3)
(vai 0)
2102(3)
+ 21(3)
2200(3)
Exerc´ıcio 2.1.8 Justifique que se x e y são inteiros positivos representados na base b por
xkxk−1 . . . x1x0 e ymym−1 . . . y1y0 respectivamente então spsp−1 . . . s1s0, a representa¸cão na
base b de x+y, pode ser obtida por um processo análogo ao descrito acima, ou seja, seguindo
o algoritmo habitual. Comece por notar que quando soma xi com yi o resultado é sempre
menor ou igual que 2b − 2, e portanto tanto xi + yi como xi + yi + 1 se representa como
0si ou 1si (pelo que ou “vai 0” ou “vai 1”), qualquer que seja i. Depois, use a defini¸cão de
representa¸cão na base b, à semelhan¸ca do que se fez acima para b = 3.
Os algoritmos usuais para adi¸cão e multiplica¸cão base 10 são válidos quando se usam
representa¸cões em qualquer outra base b, embora sejam obviamente diferentes as tabuadas
dessas opera¸cões se escrevermos os resultados na base b. O mesmo se pode dizer para a
subtraçcão (quando o aditivo é maior do que subtractivo) e para a divisão inteira.

Tabuadas de adi¸cão e multiplica¸cão para binário:
+2 0 1
0 0 1
1 1 10
×2 0 1
0 0 0
1 0 1
Tabuadas de adi¸cão e multiplica¸cão para base 3:
+3 0 1 2
0 0 1 2
1 1 2 10
2 2 10 11
×3 0 1 2
0 0 0 0
1 0 1 2
2 0 2 11
Tabuadas de adi¸cão e multiplica¸cão para octal:
+8 0 1 2 3 4 5 6 7
0 0 1 2 3 4 5 6 7
1 1 2 3 4 5 6 7 10
2 2 3 4 5 6 7 10 11
3 3 4 5 6 7 10 11 12
4 4 5 6 7 10 11 12 13
5 5 6 7 10 11 12 13 14
6 6 7 10 11 12 13 14 15
7 7 10 11 12 13 14 15 16
×8 0 1 2 3 4 5 6 7
0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7
2 0 2 4 6 10 12 14 16
3 0 3 6 11 14 17 22 25
4 0 4 10 14 20 24 30 34
5 0 5 12 17 . . . . . . . . . . . . . . .
6 0 6 . . . . . . . . . . . . . . . . . . . . . . . .
7 0 7 . . . . . . . . . . . . . . . . . . . 61
Exerc´ıcio 2.1.9 Complete a tabuada de multiplica¸cão base 8 e determine as tabelas para a
base hexadecimal.
Assim, por exemplo, 1021(3) × 211(3) = 1000201(3), ou seja, 34(10) × 22(10) = 748(10),
porque:
1 0 2 1(3)
× 2 1 1(3)
1 0 2 1
1 0 2 1
+ 2 1 1 2
1 0 0 0 2 0 1(3)
3 4(10)
× 2 2(10)
6 8
+ 6 8
7 4 8(10)
À esquerda, todos os valores intermédios estão representados na base 3 e à direita na base 10
(visando recordar o algoritmo da multiplica¸cão e estabelecer a compara¸cão).

Exerc´ıcio 2.1.10 Calcule:
(i) 1110010(2) + 111001111(2) em binário.
(ii) 1F5(h) + 111001111(2) em hexadecimal.
(iii) 1330(4) + 123(4) em octal.
(iv) 1F5(h) + ABCD(h) + 1FB(h) em hexadecimal.
(v) ABCD(h) − 1FB(h) em hexadecimal.
(vi) 73542(o) × 27(10) em octal.
(vii) 73542(o)/27(10) em octal.
(viii) 111000010(2) /111(2) em binário.
2.1.3 Representa¸cão de números com um número fixo de d´ıgitos
Num computador cada inteiro é representado por um número fixo de bits. Em 8 bits, 13 seria
representado por 00001101. Isto é, introduzem-se 0’s à esquerda sempre que o número de bits
da representa¸cão do inteiro seja menor que o número de bits que se fixou.
Se n representar o número de bits que se fixou para a representa¸cão, os bits são numerados
da esquerda para a direita por bitn−1, bitn−2, . . . , bit1 e bit0. O bitn−1 diz-se o bit mais
significativo e bit0 é o menos significativo.
Quando se fixa o número de bits da representa¸cão, limita-se também os valores que podem
ser representados. Se, por exemplo, o número de bits for 8 então o maior inteiro positivo que
se pode representar é:
1 1 1 1 1 1 1 1
bit 7 bit 6 bit 5 bit 4 bit 3 bit 2 bit 1 bit 0
cujo valor é
27
× 1 + 26
× 1 + 25
× 1 + 24
× 1 + 23
× 1 + 22
× 1 + 21
× 1 + 20
× 1 = 255 = 28
− 1
Em geral, com n bits podemos representar números inteiros positivos de 0 a 2n − 1.
Proposi¸cão 3 O maior inteiro positivo que se consegue representar na base b com n d´ıgitos
é bn − 1.

Prova: Suponhamos que A é representado com n d´ıgitos na base b por an−1an−2 . . . a1a0
com ai ∈ {0, . . . , b − 1}. Então,
A = an−1bn−1
+ an−2bn−2
. . . a1b1
+ a0b0
=
n−1
i=0
aibi
Ora,
n−1
i=0
aibi
≤
n−1
i=0
(b − 1)bi
= (b − 1)
n−1
i=0
bi
= (b − 1)
b0 − b × bn−1
1 − b
(soma de termos de progressão geométrica)
= (b − 1)
1 − bn
1 − b
= bn
− 1
Observa¸cão: n−1
i=0 ui é uma nota¸cão abreviada para u0 + u1 + · · · + un−1, podendo-se ler
“somatório para i desde 0 até n − 1 de ui”.
Exerc´ıcio 2.1.11 Qual é o número m´ınimo de bits necessário para representar 1125? Qual
o valor máximo que pode ser representado com esse número de bits?
Normalmente o número de bits usados são 8, 16, 32 ou 64. Com 8 bits podemos representar
inteiros entre 0 e 255, com 16 bits entre 0 e 65535, com 32 bits entre 0 a 4294967295, etc.
2.1.4 Representa¸cão de números negativos
Para representar números inteiros positivos e negativos numa base b e com um número fixo
de d´ıgitos é necessário codificar o sinal e encontrar um processo eficiente de determinar se
um número é positivo ou negativo. Normalmente é reservado um d´ıgito para indicar o sinal.
Por exemplo, em n d´ıgitos, sendo A = an−1an−2 . . . a1a0(b), se an−1 = 0 então A é positivo,
se an−1 = b − 1 o número é negativo.
Vamos considerar três formas introduzidas para representar números inteiros positivos e
negativos e que obedecem à condi¸cão de sinal apresentada. Vamos supor que a base é 2 e que
o número de d´ıgitos é n, embora os resultados possam ser generalizados para qualquer base b.

Representa¸cão com bit de sinal. Reserva-se o bit mais à esquerda para o sinal e os
restantes para o módulo do número.
n bits
n−1 n−2 . . . . . . . . 0
sinal módulo
O bit de sinal é 0 para os positivos e é 1 para os negativos. Assim, um número positivo
é da forma A = 0an−2 . . . a1a0 e um negativo é da forma A = 1an−2 . . . a1a0. Com n bits
podemos representar números positivos de 0 a 2n−1 − 1 e negativos −(2n−1 − 1) a 0.
As representa¸cões de dois números com o mesmo módulo diferem apenas no bit de sinal.
Se n = 3 temos o quadro seguinte:
Valor 0 1 2 3 −0 −1 −2 −3
Representa¸cão com bit de sinal 000 001 010 011 100 101 110 111
Podemos observar que zero tem duas representa¸cões: +0 e −0. Para efectuar adi¸cões
de números com sinais diferentes é necessário primeiro determinar qual é o maior e qual o
sinal do resultado. O mesmo problema surge para a subtraçcão, a qual pode ser tratada como
a adi¸cão associando o sinal negativo ao subtraendo, x − y = x + (−y).
Representa¸cão em Complemento para 1. A utiliza¸cão desta representa¸cão para inteiros
apresenta o mesmo problema da anterior, isto é, zero terá duas representa¸cões +0 e −0. Para
uma representa¸cão em n bits, chama-se complemento para 1 de A ao valor (2n − 1) − A.
O bit mais signficativo dá indica¸cão sobre o sinal do número (se for 1, o número é negativo).
O número negativo −x será representado por (2n − 1) − x. Por exemplo, para n = 3, temos
o quadro seguinte:
Valor +0 +1 +2 +3 −3 −2 −1 −0
Complemento para 1 000 001 010 011 100 101 110 111
Estas representa¸cões podem ser obtidas por troca de 1’s por 0’s e 0’s por 1’s na repre-
senta¸cão de x em n bits, o que resulta de 2n − 1 ser representado por n 1’s. Por exemplo, -14
é representado em complemento para 1 em 8 bits por:
1 1 1 1 1 1 1 1
− 0 0 0 0 1 1 1 0
1 1 1 1 0 0 0 1

Representa¸cão em Complemento para 2. Neste caso, zero terá uma só representa¸cão:
Exactamente metade dos números representados são não negativos e a outra metade números
negativos.
De 0 a 2n−1 −1 encontram-se os números não negativos e de 2n−1 a 2n −1 números
negativos.
Para os positivos a representa¸cão coincide com a representa¸cão anterior. Os números nega-
tivos são complementos para a base. Por defini¸cão, o complemento para 2 de A numa
representa¸cão de n bits é o inteiro 2n − A.
Exemplo 7 Para n = 3 então -1 é representado por 111 pois 23 − 1 = 7. Se n = 8, o
inteiro -1 é representado por 11111111 em complemento para 2. Nnuma representa¸cão em 8
bits usando complemento para 2 o inteiro −3 é o binário correspondente a 28 − 3, ou seja
253 = 11111101.
Em resumo, temos o quadro seguinte para n = 3:
Valor 0 +1 +2 +3 −4 −3 −2 −1
Complemento para 2 000 001 010 011 100 101 110 111
Usando a defini¸cão de complemento para 2, pode-se concluir que 2n−1 representa −2n−1
pois 2n − 2n−1 = 2n−1. Por outro lado, 2n − 1 representa −1.
Proposi¸cão 4 No sistema de representa¸cão com n bits e complemento para 2 os valores
poss´ıveis dos inteiros representáveis variam de −2n−1 a 2n−1 − 1. De 0 a 2n−1 − 1 tem-se
números não negativos e de 2n−1 a 2n − 1 números negativos.
Para além de só haver um zero, neste caso todos os negativos têm 1 como bit mais
significativo, o qual funciona assim como bit de sinal. As adi¸cões podem ser efectuadas
sem analisar o sinal dos operandos e nas subtraçcões basta calcular o complemento para 2 do
subtraendo e adicionar o valor resultante ao subtractivo, como se verá adiante.
Para determinar representa¸cão em complemento para 2 dum número é útil observar
a sua rela¸cão com a representa¸cão em complemento para 1.
Como 2n − A = (2n − 1 − A) + 1 e 2n − 1 − A é a representa¸cão em complemento para 1,
podemos obter a representa¸cão em complemento para 2 complementando todos os d´ıgitos
de A (isto é trocando os uns com os zeros e os zeros com os uns) e adicionando depois uma
unidade.

2.2. ADIÇ ÃO E SUBTRACÇ ÃO EM N BITS 19
Exemplo 8 Para determinar a representa¸cão de -17 em complemento para 2 em 8 bits,
toma-se 00010001, troca-se 0’s por 1’s, obtendo 11101110, e soma-se 1, resultando 11101111.
Inversamente, se se pretender determinar o valor (em decimal) do inteiro que é dado em
complemento para 2 por A = an−1an−2 . . . a1a0, basta considerar que a parcela an−12n−1 é
negativa. Por exemplo,
110(2) = 1 × (−22
) + 1 × 21
+ 0 × 20
= −4 + 2 + 0 = −2(10)
Exerc´ıcio 2.1.12 Represente em complemento para 2 e com 8 bits os números inteiros se-
guintes:
(i) 25, -25, 41, 56, 19, -31, -87;
(ii) a soma dos anteriores e verifique se o resultado de somar as representa¸cões está correcto.
Exerc´ıcio 2.1.13 Suponha que a representa¸cão em complemento para dois com 4 d´ıgitos de
um inteiro é 1101. Como é a representa¸cão com:
(i) 6 d´ıgitos
(ii) 8 d´ıgitos
(iii) n d´ıgitos, com n ≥ 4.
Exerc´ıcio 2.1.14 Suponha agora que, em 4 d´ıgitos, a representa¸cão em complemento para
dois é 0101. Como responderia às al´ıneas anteriores? Em geral, dado um inteiro x represen-
tado em n d´ıgitos como procederia para obter a sua representa¸cão com mais d´ıgitos?
2.2 Adi¸cão e Subtraçcão em n Bits
2.2.1 Adi¸cão e subtraçcão binária de inteiros não negativos
• Adi¸cão: Segue o algoritmo habitual de adi¸cão binária; se se tiver uma representa¸cão de
m bits e a soma for superior a 2m − 1 (o maior inteiro positivo com m bits) diz-se que
há transporte (carry); Por exemplo: a soma em 8-bits dos inteiros positivos 10010000
e 11111101 é 10001101, o que está errado (tem transporte 1).
• Subtraçcão: Segue algoritmo habitual de subtraçcão binária; se o valor da diferen¸ca for
inferior a zero, diz-se que há transporte (borrow); Por exemplo: a diferen¸ca em 8-bits
10010000 − 11111101 = 10010011 o que está errado (tem transporte 1).

2.2. ADIÇ ÃO E SUBTRACÇ ÃO EM N BITS 20
2.2.2 Adi¸cão de inteiros em complemento para 2
Se os inteiros são não negativos, a soma é calculada pelo algoritmo habitual. Se a repre-
senta¸cão tiver m bits e a soma for superior a 2m−1 − 1 (o maior inteiro positivo com m bits
num sistema de complemento para 2) diz-se que há overflow, sendo indica¸cão de que o valor
obtido está errado.
Por exemplo: a soma em 8-bits e complemento para 2 de 01111111 com 00000001 é
10000000 ou seja, a soma de +127 com +1 é −128(!). Neste caso, há overflow.
Se os inteiros são ambos negativos (em complemento para 2) a soma é calculada pelo
algoritmo habitual ”desprezando-se”o transporte. Se se usa uma representa¸cão em m bits,
o ”desprezar”o transporte corresponde a subtrair ao resultado obtido 2m. Basta notar que
quando se efectua (−x) + (−y) se pretende obter o complemento para 2 de x + y, isto é
2m − (x + y). A rela¸cão desse número com os complementos para 2 de x e y é 2m − (x + y) =
(2m − x) + (2m − y) − 2m. Ou seja, para obter a representa¸cão em complemento para 2 de
(−x) + (−y) adicionam-se as representa¸cões de (−x) e (−y) e subtrai-se 2m.
Se a representa¸cão tiver m bits e a soma for inferior a −2m−1 (o menor inteiro negativo
com m bits num sistema de complemento para 2) diz-se que há underflow, sendo indica¸cão
de que o valor obtido está errado.
Por exemplo: a soma em 8-bits e complemento para 2 de 10000000 com 11111111 seria
01111111 ou seja, −128 + (−1) = +127 (!). Neste caso, há underflow.
Analogamente, a soma dum inteiro positivo com um inteiro negativo é o binário correspon-
dente à adi¸cão das representa¸cões dos operandos, ”desprezando-se”o transporte se o houver.
Não haverá overflow nem underflow.
2.2.3 Subtraçcão de inteiros em complemento para 2
A subtraçcão binária de inteiros representados em complemento para 2 pode-se reduzir à
adi¸cão de inteiros.
Exemplos
(-x)-(-y) = (-x)+y 10010000-11111101=10010000+00000011=10010011
(-x)-y=(-x)+(-y) 10010000-00000011=10010000+11111101=10001101
y-(-x)=y+x 00000011-10010000=00000011+ 01110000=01110011
y-x=y+(-x) 00000011-00010000=00000011+11110000=11110011
Exerc´ıcio 2.2.1 Quais das seguintes somas estão correctas (se truncadas a 8 bits) caso as
representa¸cões indicadas sejam representa¸cões em complemento para 2 e caso sejam repre-
senta¸cões só para inteiros não negativos?

2.3. REPRESENTAÇ ÃO EM VÍRGULA FIXA 21
negativos negativo e positivo positivos
10010000
+ 11111101
1 10001101
00010000
+ 11111111
1 00001111
00010000
+ 00111101
0 01001101
positivos negativos
01111010
+ 01110001
0 11101011 < 0
10000110
+ 10001111
1 00010101 > 0
overflow underflow
2.3 Representa¸cão em V´ırgula Fixa
A representa¸cão posicional de inteiros pode ser generalizada para representar números racio-
nais considerando-se potências negativas da base. Por exemplo, na base 10:
344.45 = 3 × 102
+ 4 × 101
+ 4 × 100
+ 4 × 10−1
+ 5 × 10−2
Podemos ainda escrever:
344.45 = 34445. × 10−2
= (3 × 104
+ 4 × 103
+ 4 × 102
+ 4 × 101
+ 5 × 100
) × 10−2
Se se fixar a posi¸cão da v´ırgula (neste caso o factor é 10−2), o número pode ser tratado
como um inteiro. Assim as opera¸cões com números racionais podem ser feitas internamente
como opera¸cões com inteiros, desde que os factores de ajuste sejam guardados para que o
resultado final seja correctamente calculado.
Note-se em particular que as representa¸cões de inteiros em computadores estudadas anteri-
ormente são representa¸cões em v´ırgula fixa, com a v´ırgula à direita do bit menos significativo.
No caso geral, os ajustes da posi¸cão da v´ırgula e o seu armazenamento ficarão a cargo do
programador.
Contudo, actualmente, a representa¸cão em computadores dos números racionais é feita,
geralmente, em v´ırgula flutuante.
2.4 Representa¸cão em V´ırgula Flutuante
A representa¸cão dum número racional em v´ırgula flutuante, contrariamente à representa¸cão
em v´ırgula fixa, é feita através de um par de inteiros que representam respectivamente a
mantissa m e o expoente e de forma que para uma determinada base b, o seu valor é:

2.4. REPRESENTAÇ ÃO EM VÍRGULA FLUTUANTE 22
F = m × be
Por exemplo, 673 × 1014.
A designa¸cão v´ırgula flutuante resulta do facto de que a posi¸cão da v´ırgula depender do
expoente e portanto não ser fixada previamente.
A nota¸cão mais usada para v´ırgula flutuante é a do IEEE (Institute of Electrical and
Electronics Engineers). A base é a binária. Em precisão simples cada número é representado
com 32 bits:
S E (8 bits) M (23 bits)
O sinal da mantissa é representado pelo bit S, que por questões de eficiência é separado
da representa¸cão do módulo da mantissa o qual é constitu´ıdo pelos 23 bits mais à direita. O
valor do módulo da mantissa é normalmente dado por 1.M(2), isto é, 1 mais o valor de M
considerado como número racional binário, com a v´ırgula à esquerda do bit mais significativo.
Os oito bits restantes são interpretados como um inteiro positivo E e representam o expoente
cujo valor é E − 127. O valor representado é
F = (−1)S
(2E−127
)(1.M)(2)
excepto se E for 0000000 então F = (−1)S(2−127)(.M(2)) e se M também é zero então F = 0.
A sequência 1 10000111 10100000000000000000000 representaria um número negativo,
dado que S = 1. Como 10000111(2) = 135(10), o expoente é 135 − 127 = 8; e o módulo da
mantissa é
1 + 0.101(2) = 1 + 1 × 2−1
+ 1 × 2−3
= 1 + (5/8) = 1 + 0.625 = 1.625
O valor representado é −28 × 1.625 = −416.
Existem outras representa¸cões em v´ırgula flutuante IEEE, como a precisão dupla em que
são usados 64 bits e a quádrupla em que são usados 128 bits.
Exerc´ıcio 2.4.1 Determine qual o maior número que é representável em precisão simples,
segunda a norma do IEEE.
Exerc´ıcio 2.4.2 Indique o valor das seguintes representa¸cões em precisão simples segunda a
norma do IEEE:
(i) 0 01110101 01010100000000000000000000
(ii) 1 00101010 11100000000000000000000000
Exerc´ıcio 2.4.3 Exprima o mais exactamente poss´ıvel os seguintes números em precisão
simples IEEE: 2.5, .0005, 2−40 e 256

Cap´ıtulo 3
Algumas No¸cões de Divisibilidade
Por defini¸cão, um inteiro a é divis´ıvel por um inteiro b se e só se a = bq para algum inteiro q.
Nesse caso, escreve-se b | a, lendo-se b divide a. Também se diz que b é divisor de a e
que a é múltiplo de b. O inteiro q é o quociente da divisão inteira de a por b. Atendendo
à defini¸cão de divisor, se a = bq então tanto b como q são divisores de a. Por exemplo, os
divisores positivos de 30 são 1, 2, 3, 5, 6, 10, 15 e 30, encontrando-se emparelhados.
1 30
2 153 10
5 6
Na procura de divisores de a, para a positivo, não é necessário ultrapassar
√
a, pois qualquer
divisor que seja superior a
√
a terá que emparelhar com algum divisor que é inferior a
√
a.
3.1 Bases de Numera¸cão e Critérios de Divisibilidade
É conhecido que, um inteiro positivo representado na base 10 é divis´ıvel por 100 se e só se a
sua representa¸cão terminar por 00 (pois os restos da divisão por 10 e 102 são 0). É divis´ıvel
por 1000 sse tal representa¸cão terminar em 000. De modo análogo se pode concluir que um
inteiro (positivo) representado na base 2 é divis´ıvel por 4 (isto é, por 22) se a sua representa¸cão
em binário terminar por 00 e é divis´ıvel por 8 (isto é, por 23) sse terminar em 000.
Proposi¸cão 5 Um inteiro (positivo) x representado numa certa base b é divis´ıvel por bk,
sendo k inteiro positivo fixo, se e só a representa¸cão de x na base b terminar por k zeros.

3.1. BASES DE NUMERAÇ ÃO E CRITÉRIOS DE DIVISIBILIDADE 24
Ideia da prova: Para que x seja divis´ıvel por bk então terá que ser divis´ıvel também por
b1, b2, . . . , bk−1, o que quer dizer que se efectuar k divisões sucessivas por b terá k restos 0.
Ou seja, x = b(x/b) + 0. Depois, k > 1, também (x/b) = b((x/b)/b) + 0, . . .
Analisando a defini¸cão de representa¸cão base 10, podemos justificar o seguinte critério de
divisibilidade por 9.
Proposi¸cão 6 Um inteiro é divis´ıvel por 9 sse a soma dos d´ıgitos da sua representa¸cão na
base 10 for divis´ıvel por 9.
Prova: Seja x um inteiro (positivo) qualquer e suponhamos que a sua representa¸cão
base 10 é anan−1 . . . a1a0. Isto quer dizer que,
x = an × 10n
+ an−1 × 10n−1
+ · · · + a1 × 10 + a0
Como
10 = 9 + 1 um múltiplo de 9 mais uma unidade
...
10n = 99 . . . 9
9 repetido n vezes
+1 um múltiplo de 9 mais uma unidade
então x = (˙9 + 1) × an + (˙9 + 1) × an−1 + · · · + (˙9 + 1) × a1 + a0, ou seja
x = ˙9 + (an + an−1 + · · · + a1 + a0)
em que ˙9 é abreviatura de “um múltiplo de 9” (nesta igualdade, cada ocorrência de ˙9 designa
um múltiplo diferente). Na “simplifica¸cão” da igualdade, usámos também o facto da soma
de múltiplos de 9 ser um múltiplo de 9 e do produto dum número qualquer por um múltiplo
de 9 ser um múltiplo de 9. Observando que x = ˙9 + (an + an−1 + · · · + a1 + a0), concluimos
que x é múltiplo de ˙9 se e só se an + an−1 + · · · + a1 + a0 for múltiplo de ˙9.
O exerc´ıcio seguinte pode ser resolvido por aplica¸cão dum racioc´ınio análogo, agora obser-
vando que 10 = ˙11−1, 100 = ˙11+1, 1000 = ˙11−1, 1000 = 1000×10 = ( ˙11−1)( ˙11−1) = ˙11+1,
10000 = ( ˙11 + 1) × 10 = ˙11 − 1, . . .
Exerc´ıcio 3.1.1 Mostre que um inteiro é divis´ıvel por 11 sse a soma dos d´ıgitos de ordem
par da sua representa¸cão na base 10 for igual à soma dos d´ıgitos de ordem ´ımpar.

3.2. NOÇ ÃO DE DIVISOR E DE M ÚLTIPLO 25
Exerc´ıcio 3.1.2 Mostre que um inteiro
(i) é divis´ıvel por 5 sse a sua representa¸cão decimal terminar em 0 ou 5;
(ii) é divis´ıvel por 3 sse a soma dos d´ıgitos da sua representa¸cão decimal for divis´ıvel por 3.
(iii) é divis´ıvel por 2 sse o d´ıgito menos significativo da sua representa¸cão decimal for par.
3.2 No¸cão de Divisor e de Múltiplo
O conjunto1 dos divisores dum inteiro a é constitu´ıdo por todos os inteiros positivos tais que
se b | a e os seus simétricos.
{divisores de a} = {b : b ∈ Z e b divide a}
Frequentemente, o termo divisor é usado para referir divisor positivo.
O conjunto dos múltiplos de b é constitu´ıdo pelos inteiros da forma bz para z inteiro, ou
seja
{múltiplos de b} = {bz : z ∈ Z}.
Para mostrar formalmente o resultado seguinte basta usar a defini¸cão de múltiplo e de
divisor que acabámos de apresentar. Este resultado foi utilizado na seçcão anterior, devendo
ser bem conhecido.
Proposi¸cão 7 A soma, a diferen¸ca e o produto de dois múltiplos de b é um múltiplo de b.
O produto dum múltiplo de b por qualquer inteiro é um múltiplo de b.
Prova: Sejam m1 e m2 múltiplos de b. Então existem inteiros z1 e z2 tais que m1 = bz1
e m2 = bz2. Logo, m1 + m2 = bz1 + bz2 = b(z1 + z2) e como a soma de inteiros é um inteiro,
conclui-se que z1 +z2 ∈ Z, pelo que m1 +m2 é da forma bz, para algum z ∈ Z (concretamente,
para z = z1 + z2). Portanto, a soma de múltiplos de b é múltiplo de b.
Para mostrar que a diferen¸ca de dois múltiplos de b (isto é, m1 − m2) é múltiplo de b
procede-se analogamente.
Para mostrar que m1m2 é múltiplo de b, isto é, que o produto de dois múltiplos de b é
múltiplo de b, observe-se que m1m2 = (bz1)(bz2) = b(bz1z2) e como bz1z2 ∈ Z, conclui-se que
m1m2 é produto de b por um inteiro, ou seja, é múltiplo de b.
Do mesmo modo, para concluir que o produto dum múltiplo de b (por exemplo, m1) por
um qualquer inteiro x é múltiplo de b, basta notar que m1x = (bz1)x = b(z1x) e z1x ∈ Z.
1 É usual representar “o conjunto dos x’s tais que x satisfaz condi¸cão. . . ” por {x | x satisfaz condi¸cão . . . }.
Neste cap´ıtulo, usaremos a nota¸cão alternativa {x : x satisfaz condi¸cão . . . }, para evitar usar | com duplo
significado, reservando | para “divide”.

3.3. FACTORIZAÇ ÃO EM PRIMOS 26
Exerc´ıcio 3.2.1 Mostrar que quaisquer que sejam x, y e z inteiros, se x dividir y e dividir
y + z então também divide z.
3.3 Factoriza¸cão em Primos
Um número p é primo se e só se tem exactamente quatro divisores (inteiros), nomeadamente,
p, −p, 1 e −1. Assim, um número é primo se e só se tem exactamente dois divisores positivos.
Proposi¸cão 8 Qualquer inteiro maior do que 1 é ou primo ou produto de primos.
Prova: Pela defini¸cão de primo, tem-se 2 é primo.
Seja x ∈ N tal que x > 2. Suponhamos que já mostrámos que todo y ∈ N tal que 2 ≤ y < x
é ou primo ou produto de primos. Vamos mostrar que então também podemos concluir que
x é primo ou produto de primos. De facto, se x não for primo, existem x1, x2 ∈ N {0, 1}
tais que x = x1x2. Como 2 ≤ x1 < x e 2 ≤ x2 < x, sabemos já que x1 é primo ou produto de
primos e x2 é primo ou produto de primos.
Analisando os quatro casos (a) x1 e x2 primos, (b) x1 e x2 produtos de primos, (c) x1
primo e x2 produto de primos, e (d) x1 produto de primos e x2 primo, concluimos que se
x = x1x2 então x pode escrever-se como produto de primos. Logo, se x não é primo então x
é um produto de primos, ou seja, x é primo ou produto de primos.
A técnica utilizada na prova anterior designa-se por indu¸cão matemática. Como
hipótese de indu¸cão supusemos que já se tinha mostrado que todo y ∈ N tal que 2 ≤ y < x ou
é primo ou é produto de primos. Como x está fixo (e é finito), essa prova pode ser realmente
reconstru´ıda. Por exemplo, se x fosse 24, estariamos a assumir que já tinhamos verificado que
2, 3, 5, 7, 11, 13, 17, 19 e 23 são primos e que 4 = 2 × 2, 6 = 2 × 3, 8 = 2 × 2 × 2, 9 = 3 × 3,
10 = 2 × 5, 12 = 2 × 2 × 3, 14 = 2 × 7, 15 = 3 × 5, 16 = 2 × 2 × 2 × 2, 18 = 2 × 3 × 3,
20 = 2 × 2 × 5, 21 = 3 × 7 e 22 = 2 × 11. Como 24 não é primo porque, por exemplo,
24 = 4 × 6, então podemos concluir que é produto de primos, por substitui¸cão de 4 e 6 (que
correspondem a x1 e x2) pelas suas factoriza¸cões em primos: 24 = (2 × 2) × (2 × 3).
Usualmente, escreve-se 24 = 23 × 3, sendo esta a factoriza¸cão de 24 primos. Em geral,
para qualquer número natural n não inferior a 2, existem primos p1, . . . pk únicos e tal que n
se pode factorizar de forma única como pα1
1 × · · · × pαk
k sendo αi = 0 e pi < pj se i < j, para
todo i ≤ k e todo j ≤ k. Por exemplo, 37268 = 22 × 71 × 113 e 500 = 22 × 53.

3.3. FACTORIZAÇ ÃO EM PRIMOS 27
Corolário 8.1 Seja x um inteiro tal que x ≥ 2 e x não é primo. A factoriza¸cão de x em
primos é única, a menos de reordena¸cão dos factores.
Ideia da prova: Análoga à anterior, supondo como hipótese já se provou que todo
y ∈ N tal que 2 ≤ y < x ou é primo ou se escreve de forma única como produto de primos (a
menos de reordena¸cão de factores).
Corolário 8.2 Qualquer inteiro maior do que 1 que não é primo é divis´ıvel por algum primo.
Prova: Seja x um inteiro qualquer maior do que 1. Se x não é primo então x é produto
de primos. Consequentemente, algum primo é seu divisor.
Proposi¸cão 9 O conjunto dos inteiros não negativos que são primos é infinito.
Prova: Suponhamos que só existiam n primos, sendo n um certo inteiro fixo. Ou seja,
suponhamos que o conjunto dos primos era finito e que tinha exactamente n elementos, os
quais vamos denotar por p1, p2, . . . , pn. Então, o inteiro positivo
1 +
n
i=1
pi
não seria primo, já que é maior do que qualquer um dos primos p1, p2, . . . , pn.
Mas se 1 + p1p2 . . . pn não é primo, então algum dos primos o divide (ou seja, é múltiplo
de algum dos primos). Suponhamos que pk divide 1 + p1p2 · · · pn, sendo k um inteiro fixo,
1 ≤ k ≤ n. Como pk divide n
i=1 pi isto é, pk divide o produto 1+p1p2 · · · pn, pode-se concluir
que se pk dividir 1 + p1p2 · · · pn então pk divide 1. Mas nenhum primo divide 1. O absurdo
resultou de se ter suposto que o conjunto dos primos era finito. Logo, o conjunto dos primos
é infinito.
3.3.1 Determina¸cão de primos: crivo de Erastótenes
Descreve-se a seguir um algoritmo para determina¸cão de todos os primos não superiores a
um número n dado. Tal algoritmo é conhecido como método do crivo. Parte-se duma tabela
contendo todos os números não superiores n. O algoritmo resume-se a seleccionar o menor
inteiro na tabela (ainda não seleccionado) e apagar todos os seus múltiplos até todos os valores
estarem ou seleccionados ou apagados.
2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
2 3 5 7 9
11 13 15 17 19
21 23 25 27 29
31 33 35 37 39
41 43 45 47 49

3.4. MÁXIMO DIVISOR COMUM 28
2 3 5 7 9
11 13 15 17 19
21 23 25 27 29
31 33 35 37 39
41 43 45 47 49
2 3 5 7
11 13 17 19
23 25 29
31 35 37
41 43 47 49
2 3 5 7
11 13 17 19
23 29
31 37
41 43 47 49
2 3 5 7
11 13 17 19
23 29
31 37
41 43 47
O processo continua . . . Os valores que ficarem na tabela são os primos, neste caso, não
superiores a 50 (o valor de n neste exemplo).
3.3.2 Cálculo de divisores por análise da factoriza¸cão em primos
A partir da factoriza¸cão dum número em primos é poss´ıvel determinar todos os seus divisores.
Por exemplo, os divisores de 30, que é dado por
30 = 21
× 31
× 51
são:
20 × 30 × 50 = 1 21 × 30 × 50 = 2 20 × 31 × 50 = 3
20 × 30 × 51 = 5 21 × 31 × 50 = 6 21 × 30 × 51 = 10
20 × 31 × 51 = 15 21 × 31 × 51 = 30
Em geral, se pα1
1 · · · pαk
k for a decomposi¸cão de x em primos então o conjunto dos divisores
positivos de x é
{pβ1
1 · · · pβk
k : 0 ≤ βi ≤ αi para i = 1, . . . , k}
concluindo-se que o número de divisores de pα1
1 · · · pαk
k é k
i=1(αi + 1).
3.4 Máximo Divisor Comum
Sabemos que 1 é divisor de qualquer inteiro e que o maior divisor de qualquer inteiro positivo x
é o próprio x. Dados inteiros positivos a e b, podemos falar do seu máximo divisor comum,
o qual representamos por mdc(a, b). O máximo divisor comum é o maior dos divisores comuns:

d é mdc(a, b) sse d | a, d | b e d | d qualquer que seja d tal que d | a e d | b. Por defini¸cão de
mdc(a, b), cada divisor comum de a e b é divisor de mdc(a, b).
Por exemplo, por análise da decomposi¸cão de 30 e 500 em primos, 30 = 2 × 3 × 5 e
500 = 22 × 53, podemos concluir que mdc(30, 500) = 10.
Dois inteiros a e b chamam-se primos entre si se e só se mdc(a, b) = 1.
Proposi¸cão 10 Os inteiros a/mdc(a, b) e b/mdc(a, b) são primos entre si.
Prova: Queremos mostrar que mdc( a
mdc(a,b) , b
mdc(a,b) ) = 1. Para isso vamos provar que
se mdc( a
mdc(a,b) , b
mdc(a,b) ) = d então mdc(a, b)d também divide a e b. Podemos depois concluir
que necessariamente d = 1 pois se d fosse maior do que 1 então mdc(a, b)d > mdc(a, b),
mdc(a, b)d seria um divisor comum a a e b, maior do que o máximo divisor comum, o que,
por defini¸cão de mdc(a, b) é imposs´ıvel. Para completar os detalhes da prova, resta mostrar
que mdc(a, b)d é divisor de a e de b se d | a
mdc(a,b) e d | b
mdc(a,b) . De facto, basta notar que:
a = mdc(a, b)
a
mdc(a, b)
= mdc(a, b)d
a
mdc(a, b)d
e
b = mdc(a, b)
b
mdc(a, b)
= mdc(a, b)d
b
mdc(a, b)d
.
Tem-se mdc(320 ×57 ×1127 ×312, 24 ×36 ×525) = 36 ×57, porque o máximo divisor comum
é dado por
2min(0,4)
× 3min(20,6)
× 5min(7,25)
× 11min(27,0)
× 31min(2,0)
ou seja, por 203657110310. Este método pode ser sempre aplicado se forem conhecidas as
factoriza¸cões dos números a e b. Quando não se conhecem, o algoritmo de Euclides
permite calcular mdc(a, b) eficientemente.
3.4.1 Cálculo do máximo divisor comum pelo algoritmo de Euclides
A correçcão do algoritmo de Euclides para cálculo do mdc(a, b) decorre do seguinte resultado.
Lema 1 Sejam a e b inteiros positivos tais que a < b e seja r o resto da divisão de a por b.
Então, mdc(a, b) = mdc(b, r).
Prova: Represente-se por d o máximo divisor comum de a e b. Por defini¸cão de divisão
inteira, r é o resto da divisão de a por b sse 0 ≤ r < b e a = bq + r para algum q ∈ Z. Por
outro lado, por defini¸cão de máximo divisor comum, d|a e d|b. Portanto, d|(a − bq). Ou seja,

d|r. Logo, d é um divisor comum de b e r. Seja d um outro divisor comum de b e de r.
Resta-nos mostrar que d terá que dividir d para poder concluir que d é mdc(b, r). Para isso,
basta notar que se d |b e d |r então d |(bq + r) e portanto d |a. Logo, d é um divisor comum
a a e b, e portanto d |mdc(a, b), isto é, d |d.
Algoritmo de Euclides para determina¸cão de mdc(a, b). Sendo a e b inteiros positivos,
podemos definir mdc(a, b) recursivamente por
mdc(a, 0) = a se a > 0
mdc(a, b) = mdc(b, a%b) se a > b > 0
mdc(a, b) = mdc(b, a) se a < b
em que a%b denota o resto da divisão de a por b.
Por exemplo, mdc(30, 500) = mdc(500, 30) = mdc(30, 500%30) = mdc(30, 20) = mdc(20, 10) =
mdc(10, 0) = 10.
500 30
20 16
30 20
10 1
20 10
0 2
Observe-se que mdc(500, 30) = 17 × 30 − 1 × 500 já que
10 = 30 − 1 × 20 = 30 − (500 − 16 × 30) = 17 × 30 − 1 × 500
ou seja, mdc(500, 30) pode-se escrever na forma 500x + 30y para x, y ∈ Z apropriados.
Lema 2 Quaisquer que sejam a, b ∈ Z+, existem inteiros x e y tais que ax + by = mdc(a, b),
ou seja, mdc(a, b) é combina¸cão linear inteira de a e b.
Para escrever mdc(100, 17) (isto é, 1) como combina¸cão de 100 e 17, observe-se que:
100 17
15 5
17 15
2 1
15 2
1 7
2 1
0 2
Efectuando análise para trás, substituindo sucessivamente os restos de forma a conseguir
fazer aparecer 100 e 17 (a e b iniciais) obtem-se a combina¸cão procurada: 1 = 15 − 7 × 2 =
15 − 7(17 − 1 × 15) = 8 × 15 − 7 × 17 = 8(100 − 5 × 17) − 7 × 17 = 8 × 100 − 47 × 17.
Proposi¸cão 11 Sendo a, b e c constantes inteiras, a equa¸cão ax + by = c com x, y ∈ Z, tem
solu¸cão se e só se mdc(a, b) | c.

3.5. MÍNIMO M ÚLTIPLO COMUM 31
Prova: Como mdc(a, b) divide a e divide b, também divide ax + by quaisquer que sejam
x, y ∈ Z. Portanto, para que ax + by = c tenha solu¸cão é necessário que mdc(a, b) divida c.
Por outro lado, usando o facto de mdc(a, b) se poder escrever como combina¸cão inteira
de a e de b, temos mdc(a, b) = ama + bmb para ma e mb inteiros adequados. Se mdc(a, b) | c,
então c = mdc(a, b) c
mdc(a,b) e c
mdc(a,b) ∈ Z. Multiplicando mdc(a, b) = ama + bmb por c
mdc(a,b)
obtem-se mdc(a, b) c
mdc(a,b) = a(ma
c
mdc(a,b) ) + b(mb
c
mdc(a,b) ). Assim, vemos que se tomarmos
x = ma
c
mdc(a,b) e y = mb
c
mdc(a,b) temos uma solu¸cão inteira de ax + by = c.
Pode-se provar que (x, y) ∈ Z2 é solu¸cão de ax + by = c sse x = ma
c
mdc(a,b) + k b
mdc(a,b) e
y = mb
c
mdc(a,b) − k b
mdc(a,b) , com k ∈ Z qualquer.
3.5 M´ınimo Múltiplo Comum
Dados inteiros positivos a e b sabemos que ab é um múltiplo de a e de b, fazendo sentido
determinar o menor inteiro positivo que é múltiplo comum a a e b, ou seja o m´ınimo múltiplo
comum, mmc(a, b). Por defini¸cão m é mmc(a, b) sse a | m, b | m e m | m para todo m tal
que a | m e b | m . Assim, mmc(a, b) é um divisor de todos os múltiplos comuns de a e b.
Exemplo 9 mmc(320571127312, 2436525) = 2max(0,4)3max(20,6)5max(7,25)11max(27,0)31max(2,0) =
243205251127312.
Como
a
mdc(a, b)
e
b
mdc(a, b)
são primos entre si, podemos mostrar a Proposi¸cão 12.
Proposi¸cão 12 Quaisquer que sejam a, b ∈ Z+, mmc(a, b) =
ab
mdc(a, b)
.
Prova:
ab = mdc(a, b)
a
mdc(a, b)
mdc(a, b)
b
mdc(a, b)
= mdc(a, b)
a
mdc(a, b)
b
mdc(a, b)
mmc(a,b)
mdc(a, b)
Para ver que mdc(a, b) a
mdc(a,b)
b
mdc(a,b) é mmc(a, b), notemos que é múltiplo de a e de b. Por
outro lado, para verificar que divide qualquer outro múltiplo m de a e de b, escrevamos
m = k1a e m = k2b para inteiros k1 e k2 apropriados. Então, m = k1mdc(a, b) a
mdc(a,b) e m =
k2mdc(a, b) b
mdc(a,b) , pelo que k1
a
mdc(a,b) = k2
b
mdc(a,b) . Como b
mdc(a,b) e a
mdc(a,b) são primos entre
si, b
mdc(a,b) tem que dividir k1. Assim, k1 = b
mdc(a,b) k1 para algum k1 e consequentemente, m =
b
mdc(a,b) k1mdc(a, b) a
mdc(a,b) e portanto m é múltiplo de mdc(a, b) b
mdc(a,b)
a
mdc(a,b) . Conclui-se
que mdc(a, b) b
mdc(a,b)
a
mdc(a,b) é mmc(a, b).

3.6. CONGRUÊNCIAS 32
3.6 Congruências
Dados b ∈ Z+ e x, y ∈ Z dizemos que x e y são congruentes módulo b se e só se x − y for
múltiplo de b, escrevendo x ≡ y (mod b). Tal é equivalente a dizer que x e y dão o mesmo
resto quando divididos por b. De facto, se x = qxb + rx e y = qyb + ry com 0 ≤ rx < b e
0 ≤ ry < b, então x − y = (qx − qy)b + (rx − ry) e portanto x − y é múltiplo de b se e só se
rx − ry o for. Mas, como 0 ≤ rx < b e 0 ≤ ry < b, podemos concluir que −b < rx − ry < b, e
consequentemente rx − ry é múltiplo de b se e só se for zero. Portanto, x ≡ y (mod b) sse os
restos da divisão de x e y por b são iguais. (Escrevemos qx, qy e rx, ry em vez de q1, q2 e r1, r2
para indicar que esses quocientes e restos dependem de x e y respectivamente.)
As rela¸cões de congruências têm algumas propriedades interessantes (e importantes). Por
exemplo, a “congruência módulo 2” decompõe os inteiros em dois conjuntos:
{x : x ∈ Z, x ≡ 0 (mod 2)} = {2k : k ∈ Z} = {pares}
{x : x ∈ Z, x ≡ 1 (mod 2)} = {1 + 2k : k ∈ Z} = {´ımpares}
A rela¸cão de “congruência módulo b” (para b ∈ Z+) decompõe os inteiros em b conjuntos
{x : x ∈ Z, x ≡ 0 (mod b)} e {x : x ∈ Z, x ≡ 1 (mod b)}, . . . , {x : x ∈ Z, x ≡ b − 1 (mod b)},
sendo cada um identificado por um dos b restos poss´ıveis.
Outra das propriedades interessantes da rela¸cão de congruência é ser preservada pelas
opera¸cões de soma, subtraçcão e produto, ou seja, se x1 ≡ y1 (mod b) e x2 ≡ y2 (mod b) então
x1 ± x2 ≡ y1 ± y2 (mod b) e x1 × x2 ≡ y1 × y2 (mod b).
O exemplo seguinte ilustra uma das aplica¸cões de congruências.
Exemplo 10 Suponha que se quer resolver 5x + 3y = 1 para x, y ∈ Z. Como 5x + 3y = 1 ⇔
5x − 1 = 3(−y) podemos come¸car por resolver 5x ≡ 1 (mod 3). Tem-se 5x ≡ 1 (mod 3) ⇔
2x ≡ 1 (mod 3). Por outro lado, 2x ≡ 1 (mod 3) ⇔ (−1)x ≡ 1 (mod 3), ou seja x ≡ (−1) (mod 3),
isto é x ≡ 2 (mod 3). Assim, 5x ≡ 1 (mod 3) se e só se x = 2 + 3k para algum k ∈ Z.
Voltando à equa¸cão inicial, temos 5x + 3y = 1 ⇔ 5(2 + 3k) + 3y = 1 ⇔ y = −3 − 5k
concluindo-se que as solu¸cões de 5x + 3y = 1 são os pontos (x, y) da forma x = 2 + 3k e
y = −3 − 5k, com k ∈ Z.

Cap´ıtulo 4
Indu¸cão Matemática
O método de demonstra¸cão por indu¸cão matemática (ou indu¸cão finita) será bastante usado
durante o curso pelo que é conveniente introduzi-lo (ou recordá-lo).
4.1 Princ´ıpio de Indu¸cão Matemática
Imagine uma escada com uma infinidade de degraus. Não é uma escada com um número
enorme de degraus! Esta escada, tem sempre um degrau acima de qualquer outro que consi-
dere. Suponha que é verdade (4.1).
“Se conseguir chegar até um degrau, então também consigo chegar ao seguinte.” (4.1)
Se nada mais for dito, não pode concluir que “consegue chegar ao 16o
¯ degrau”.
Suponha agora não só (4.1) mas também (4.2).
“Consigo chegar ao 13o
¯ degrau” (4.2)
O que pode concluir? Como consegue chegar ao 13o
¯ e é verdade (4.1), então consegue chegar
ao 14o
¯. Como consegue chegar ao 14o
¯ e é verdade (4.1), então consegue chegar ao 15o
¯. Como
consegue chegar ao 15o
¯ e é verdade (4.1), então consegue chegar ao 16o
¯. De (4.1) e (4.2),
conclui-se (4.3).
“Consegue chegar ao n-ésimo degrau, qualquer que seja n ≥ 13.” (4.3)
Como não é dito sobre de que forma chegou ao 13o
¯ degrau, nada pode concluir sobre a
possibilidade de chegar ao degrau n, para n < 13.
Mas, suponha agora que (4.4) é verdade.
“Consigo chegar ao 1o
¯ degrau”. (4.4)

4.1. PRINCÍPIO DE INDUÇ ÃO MATEM ÁTICA 34
Do mesmo modo que anteriormente, se supuser (4.1) e (4.4) então pode concluir (4.5).
“Consegue chegar ao n-ésimo degrau, qualquer que seja n ≥ 1.” (4.5)
Proposi¸cão 13 (Princ´ıpio de Indu¸cão Matemática) Escrevamos P(n) como abreviatura
de “o inteiro não negativo n satisfaz a propriedade/condi¸cão P ”. Tem-se ∀n ∈ N P(n), se
forem satisfeitas as duas condi¸cões (i) e (ii) seguintes.
(i) P(0) é verdade;
(ii) ∀k ∈ N ( P(k) ⇒ P(k + 1) ), isto é para todo k ∈ N, se P(k) então P(k + 1);
P(0) diz-se (caso de) base de indu¸cão. Em P(k) ⇒ P(k+1), chamamos a P(k) a hipótese
de indu¸cão e a P(k + 1) a tese.
Exemplo 11 Seja An a área dum quadrado de lado 2n, com n ≥ 1 (inteiro). Vamos mostrar
que o resto da divisão de An por 3 é 1, qualquer que seja n ≥ 1.
(i) (Caso de base) Como A1 é 4 e sabemos que o resto da divisão de 4 por 3 é 1, é verdade
que a condi¸cão se verifica para n = 1.
(ii) (Hereditariedade) Mostremos que qualquer que seja k ≥ 1, se Ak for da forma 3p+1 para
algum inteiro não negativo p, então Ak+1 = 3q + 1 para algum inteiro não negativo q.
Ora, se Ak = 3p+1, então Ak+1 = (2k+1)2 = 4(2k)2 = 4Ak = 4(3p+1) = 3(4p+1)+1.
Ou seja, Ak+1 = 3q + 1 para algum inteiro não negativo, já que se p ∈ Z e p ≥ 0 então
4p + 1 ∈ Z e 4p + 1 ≥ 0.
Usando (ii) e (i) podemos concluir que qualquer que seja n ≥ 1, a área do quadrado de
lado 2n excede numa unidade um múltiplo de 3.
Observe que, se nos fosse pedido, podiamos apresentar a dedu¸cão de que A6 excede numa
unidade um múltiplo de 3:
Por (i), sabemos que o resto da divisão de A1 por 3 é 1;
De (i) e (ii), concluimos que o resto da divisão de A2 por 3 é 1;
Como o resto da divisão de A2 por 3 é 1, concluimos, por (ii), que o resto da divisão de A3 por 3 é 1;
Como o resto da divisão de A5 por 3 é 1, concluimos, por (ii), que o resto da divisão de A6 por 3 é 1.
Do mesmo modo que conseguimos mostrar que A6 dá resto 1 quando dividido por 3,
podiamos, dado um n ≥ 1, apresentar a dedu¸cão de que An dá resto 1 quando dividido por 3,
se tal nos fosse pedido.

Proposi¸cão 14 (Versão geral do Princ´ıpio de Indu¸cão) Seja n0 ∈ Z, e suponha que
P(n) denota “o inteiro n satisfaz a propriedade P. Se forem satisfeitas as duas condi¸cões (i)
e (ii) seguintes, então, para todo o inteiro n ≥ n0 tem-se P(n).
(i) P(n0) é verdade;
(ii) ∀k ≥ n0 ( P(k) ⇒ P(k + 1) ), isto é, para todo inteiro k tal que k ≥ n0, se P(k)
então P(k + 1);
Exemplo 12 Vamos mostrar que qualquer que seja n ≥ 1 e quaisquer que sejam a, b ∈ R+,
se tem (a + b)n < 2n(an + bn).
Podemos concluir isso se mostrarmos que as duas condi¸cões de aplicabilidade do princ´ıpio
de indu¸cão matemática se verificam neste caso.
(i) Para n=1, (a + b)1 = a + b < 2(a + b) = 21(a1 + b1), porque a, b ∈ R+.
(ii) Suponhamos agora que para um dado k ≥ 1 se tem (a+b)k < 2k(ak +bk), para a, b ∈ R+
quaisquer, e vamos mostrar que então (a + b)k+1 < 2k+1(ak+1 + bk+1).
Como (a + b)k+1 = (a + b)k(a + b), e por hipótese
(a + b)k
< 2k
(ak
+ bk
),
concluimos que
(a + b)k+1
< 2k
(ak
+ bk
)(a + b) = 2k
(ak+1
+ bk+1
+ ak
b + bk
a).
Como
2k
(ak+1
+ bk+1
+ ak
b + bk
a) = 2k
(ak+1
+ bk+1
) + 2k
(ak
b + bk
a),
para concluir que (a + b)k+1 < 2k+1(ak+1 + bk+1) vamos mostrar que
ak
b + bk
a ≤ ak+1
+ bk+1
quaisquer que sejam a, b reais positivos. Tem-se
ak
b + bk
a − ak+1
− bk+1
= −(ak
− bk
)(a − b) ≤ 0,
já que quaisquer que sejam x, y ∈ R+, se x ≤ y então xp ≤ yp, para todo p ≥ 1 (relembre
que as fun¸cões fp(x) = xp, são estritamente crescentes em R+).

Exerc´ıcio 4.1.1 Aplique o princ´ıpio de indu¸cão matemática para resolver os problemas se-
guintes.
a) Mostrar que |sen(nx)| ≤ n|sen(x)|, para todo x ∈ R e todo n ∈ N.
b) Mostrar que 4n + 15n − 1 é múltiplo de 9, para todo n ≥ 1.
Exemplo 13 Considere o seguinte algoritmo (imagine que Y é uma caixa1).
1. Coloque em Y o valor 0.
2. Escolha um inteiro (vamos referi-lo por X).
3. Se X = 0 então fa¸ca 7.
4. Se X > 0 então volte a 2.
5. Substitua o valor em Y pela soma do valor que lá estava com dois.
6. Volte a 2.
7. Indique o valor que guarda em Y, e páre.
O valor em Y quando se executa 7. é o dobro do número de inteiros negativos nos valores
escolhidos. Para o provar, vamos mostrar que tal propriedade caracteriza o valor de Y em
cada itera¸cão do ciclo (ou seja, é um invariante do ciclo). Usamos indu¸cão sobre o número
de itera¸cões efectuadas.
O valor que está guardado em Y quando está a executar 2. pela 2a
¯ vez é 0 se o primeiro
valor escolhido em 2. for positivo, e é 2 se tal valor for negativo.
Quando está a executar 2. pela 3a
¯ vez, o valor em Y é 4 se ambos os valores escolhidos
anteriormente forem negativos, é 2 se um for negativo e o outro positivo, e é 0 se ambos forem
positivos.
Suponhamos que para um dado k ≥ 1, quando se se está a executar 2. pela ka
¯ vez, o valor
em Y é o dobro do número de inteiros negativos nos k − 1 valores escolhidos anteriormente.
Então, por análise do algoritmo, concluimos que se se estiver a executar 2. pela (k + 1)a
¯
vez, o valor em Y é igual ao valor anterior se tivermos dado mais um número positivo, ou foi
incrementado de duas unidades, se tivermos dado mais um número negativo. Portanto, se
quando se estiver a executar 2. pela ka
¯ vez, o valor em Y é o dobro do número de inteiros
negativos nos k−1 valores escolhidos anteriormente, então quando se estiver a executar 2. pela
(k + 1)a
¯ vez, valor em Y é o dobro do número de inteiros negativos nos k valores escolhidos
anteriormente.
Consequentemente, por indu¸cão matemática, podemos concluir que o valor em Y quando
se executa 7. é o dobro do número de inteiros negativos nos valores escolhidos.
1
Na terminologia de linguagens de programa¸cão, X e Y são variáveis de programa¸cão.

4.1.1 Erros frequentes
É necessário mostrar as duas condi¸cões de aplicabilidade do princ´ıpio de indu¸cão, sem o que
as provas não ficam completas e, no pior dos casos, os resultados mal “demonstrados” são
mesmo falsos.
O exemplo seguinte serve para ilustrar o facto de certas propriedades, não observáveis,
poderem ser hereditárias. Hereditárias, no sentido de se um dado inteiro as satisfizer, também
o inteiro seguinte as satisfaz.
Exemplo 14 Considere a seguinte demonstra¸cão (claramente, errada!) de que “entre dois
inteiros consecutivos existe uma infinidade de inteiros”.
Prova: Para todo x ∈ R (em particular para x inteiro) se k ≤ x ≤ k + 1 então
k + 1 ≤ x + 1 ≤ k + 2, qualquer que seja k ∈ N. Assim, se entre k e k + 1 existir
uma infinidade de inteiros, então entre k+1 e k+2 também existe uma infinidade
de inteiros. De facto, a cada inteiro x no intervalo [k, k +1] podemos associar um
inteiro x no intervalo [k + 1, k + 2], a saber, por exemplo x é x + 1.
Logo, por indu¸cão matemática sobre k, concluimos que entre dois inteiros conse-
cutivos existe uma infinidade de inteiros.
Como entre dois inteiros consecutivos não há qualquer outro inteiro, a prova tem que estar
errada. O erro está na conclusão “precipitada”. Não se mostrou que existia um intervalo
[k, k +1] que tinha uma infinidade de inteiros. Apenas se mostrou a condi¸cão (ii) do princ´ıpio
de indu¸cão. A condi¸cão (i) não foi provada, nem se pode provar!
Exemplo 15 A demonstra¸cão seguinte está obviamente errada dado que permite concluir
que “todos os cavalos são brancos” (e, todos sabemos que há cavalos doutras cores).
Vamos mostrar que qualquer que seja o número de cavalos que estejam numa
cerca, se existir algum cavalo branco entre eles então todos os cavalos nessa cerca
são brancos.
Prova: Para isso vamos mostrar que as duas condi¸cões (i) e (ii) do princ´ıpio de
indu¸cão se verificam nessa situa¸cão.
(i) Como deve estar pelo menos um cavalo branco na cerca, podemos afirmar
que se só existir um cavalo na cerca é branco.

(ii) Fixemos um k ∈ N, e suponhamos que se existirem k cavalos numa cerca
qualquer, estando pelo menos um cavalo branco entre eles, então todos os
demais são brancos. Consideramos agora uma cerca onde estão k + 1 cavalos
sendo branco pelo menos um deles. Retiremos um cavalo da cerca deixando
ficar o branco. Dado que estão k cavalos na cerca, estando um branco entre
eles, segue pela hipótese de indu¸cão, que os k cavalos na cerca são brancos.
Resta mostrar que o cavalo que retirámos primeiramente também era branco.
Retiremos um dos cavalos que está na cerca (é indiferente qual se retira
porque de facto todos são brancos), e voltemos a colocar o que retirámos
primeiramente. Mais uma vez, pela hipótese, podemos concluir que todos os
cavalos que estão agora na cerca são brancos.
Assim, pelo princ´ıpio de indu¸cão matemática segue a validade da proposi¸cão que
queriamos mostrar.
Sabemos que “se existir algum cavalo branco numa cerca”, também lá podem estar cavalos
doutras cores. Logo, a afirma¸cão que “mostrámos” por indu¸cão é falsa. Mas, como o sistema
dedutivo que estamos a seguir é consistente, não podemos deduzir proposi¸cões falsas, pelo
que há que encontrar um erro (v´ıcio) na prova dada.
Sabemos que se estiverem dois cavalos numa cerca e um deles for branco, então isso não
implica que o outro também seja branco. Por outras palavras, é falso P(1) ⇒ P(2).
Para localizarmos o erro, vamos então seguir em detalhe a prova de (ii) para k = 1.
Fixemos k = 1. Suponhamos (podemos sempre supor o que quisermos) que é
sempre branco o cavalo que estiver sózinho numa cerca em que há pelo menos
um cavalo branco. Consideramos agora uma cerca onde estão dois cavalos sendo
branco pelo menos um deles. Retiremos um cavalo da cerca deixando ficar o
branco. Dado que está um só cavalo na cerca, estando um branco na cerca, segue
pela hipótese de indu¸cão, que o cavalo na cerca é branco. Resta mostrar que
o cavalo que retirámos primeiramente também era branco. Retiremos o cavalo
que está na cerca, e voltemos a colocar o que retirámos primeiramente. Agora
não podemos aplicar a hipótese, pois só está na cerca o cavalo que acabámos de
lá colocar, e não sabemos de que cor é (por isso não podemos afirmar que haja
algum cavalo branco na cerca).
Note que a prova de (ii) é válida para k ≥ 2, ou seja é verdade que qualquer que seja
k ≥ 2, se forem brancos os k cavalos que estiverem numa qualquer cerca onde está pelo menos
um branco, então são brancos os k + 1 cavalos que estiverem numa qualquer cerca onde está

pelo menos um branco. Conclusão: só não conseguimos mostrar que “todos os cavalos são
brancos” porque P(1) ⇒ P(2).
No exemplo2 que se segue, a prova está errada, mas o resultado é válido.
Exemplo 16 Pretendemos mostrar que qualquer que seja n ≥ 1, o quadrado de lado 2n pode
ser coberto por pe¸cas da forma seguinte, ficando apenas um quadrado 1 × 1 por cobrir.
A propriedade verifica-se para n = 1, por exemplo:
Para concluir, por indu¸cão, que a propriedade é válida para todo n ≥ 1, resta
mostrar que qualquer que seja k ≥ 1, se os quadrados de lado 2k admitem a
cobertura descrita, então os quadrados de lado 2k+1 também admitem.
Dado um quadrado de lado 2k+1 podemos dividi-lo em quatro quadrados de lado 2k
como se ilustra na figura abaixo. Por hipótese, cada quadrado de lado de 2k pode
ser coberto por pe¸cas da forma descrita acima. Fazemos para cada um dos quatro
uma tal cobertura de forma a ficarem a descoberto os quadrados 1 × 1 indicados
na figura. Verificamos que os três quadrados 1 × 1 (ao centro) podem ser cobertos
por uma pe¸ca, pelo que só fica um quadrado 1 × 1 por cobrir.
2k+1
2k
2k1
1
Esta prova não está correcta! Porquê? Na demonstra¸cão supusemos que o quadrado por
cobrir, podia estar num canto, mas o quadrado que deixámos depois a descoberto não ficou
num canto. No entanto, podemos corrigir a prova, mostrando um resultado mais forte do que
o enunciado inicialmente. . . “a cobertura pode ser tal que o quadrado 1 × 1 a descoberto fica
num canto”. Para isso, basta notar que caso n = 1, o quadrado por cobrir está num canto, e
que para mostrar que ∀n (P(n) ⇒ P(n + 1)) podemos fazer o seguinte.
2
de Maggie Johnson, Introducton to Induction, Lecture Notes CS109, 1998.

4.2. INDUÇ ÃO FORTE 40
2k+1
2k
2k
4.2 Indu¸cão Forte
Em certos casos é útil refor¸car a hipótese de indu¸cão.
Exemplo 17 Para mostrar que qualquer inteiro maior do que 1 é ou primo ou produto de
primos, fixado um k, é conveniente assumir que já se mostrou que todo i ∈ N tal que 2 ≤ i ≤ k
ou é primo ou é produto de primos porque não basta ter a decomposi¸cão de k em primos para
construir a decomposi¸cão de k + 1. A prova ficaria então:
• Pela defini¸cão de primo, 2 é primo.
• Seja k ∈ N tal que k ≥ 2. Suponhamos que já mostrámos que todo i ∈ N tal que
2 ≤ i ≤ k é ou primo ou produto de primos. Vamos mostrar que então também
podemos concluir que k + 1 é primo ou produto de primos. De facto, se k + 1 não for
primo, existem i1, i2 ∈ N {0, 1} tais que k + 1 = i1i2. Como 2 ≤ i1 ≤ k e 2 ≤ i2 ≤ k,
sabemos já que i1 é primo ou produto de primos e i2 é primo ou produto de primos.
Analisando os quatro casos (a) i1 e i2 primos, (b) i1 e i2 produtos de primos, (c) i1
primo e i2 produto de primos, e (d) i1 produto de primos e i2 primo, concluimos que se
k + 1 = i1i2 então k + 1 pode-se escrever como produto de primos. Logo, se k + 1 não
é primo, k + 1 é um produto de primos, ou seja, k + 1 é primo ou produto de primos.
Mostrámos que 2 é primo (ou produto de primos) e que qualquer que seja k ≥ 2 se todo i tal
que 2 ≤ i ≤ n for primo ou produto de primos então k + 1 é primo ou produto de primos.
Portanto, por indu¸cão, n é primo ou produto de primos, qualquer que seja n ≥ 2.
Proposi¸cão 15 (Versão forte do princ´ıpio de indu¸cão) Seja P(n) uma condi¸cão na
variável n ∈ Z. Dado n0 ∈ Z, se forem satisfeitas as duas condi¸cões (i) e (ii) seguintes, então
∀n ≥ n0 P(n).
(i) P(n0) é verdade;
(ii) para todo k ∈ Z, se se tem P(i) para todo i ∈ Z com n0 ≤ i ≤ k, tem-se P(k + 1).

Exemplo 18 Seja “QS” (é conhecido por quick-sort) o algoritmo seguinte.
0. Supõe-se dada uma sequência finita de inteiros (pode não ter elementos).
1. Se a sequência não tem qualquer elemento então indicar como resultado a
própria sequência.
2.1 Senão seja X o primeiro elemento na sequência dada.
2.2 Separar os restantes elementos da sequência formando a subsequência dos
menores do que X e a subsequência dos maiores ou iguais que X.
2.3 Aplicar “QS” a cada uma das subsequências: sejam R< e R≥ as sequências
resultantes (respectivamente).
2.4. Dar como resultado os elementos de R<, seguidos de X, seguidos dos
elementos de R≥.
O algoritmo “QS” ordena por ordem crescente a sequência finita de inteiros dada. Para o
provar, vamos usar indu¸cão sobre o número de elementos na sequência dada.
(i) Se a sequência dada não tem elementos, então podemos dizer que a sequência resultante,
que é igual à dada (por 1.) está ordenada por ordem crescente.
(ii) Seja S uma qualquer sequência de inteiros, e seja n (n ≥ 1 fixo) o seu número de
elementos. Suponhamos agora, como hipótese de indu¸cão, que quando aplicamos “QS”
a uma qualquer sequência W de inteiros cujo número de elementos é menor do que n,
obtemos os elementos de W por ordem crescente.
Queremos mostrar que “QS” quando aplicado a S, ordena S por ordem crescente.
Como S tem elementos, aplicam-se as instru¸cões 2.1–2.4. Uma vez que nas sub-
sequências formadas em 2.2 não entra o primeiro elemento de S, cada uma delas tem
menos elementos do que S. Assim, por hipótese de indu¸cão, “QS” quando aplicado a
cada uma dessas subsequências, ordena-as por ordem crescente. Então, as sequências
referidas por R< e R≥ (em 2.3) são respectivamente as sequências de elementos menores
do que X e maiores ou iguais a X, ordenadas por ordem crescente. Portanto, o resultado
indicado em 2.4 não é mais do que a sequência S ordenada por ordem crescente.
Proposi¸cão 16 Os princ´ıpios de indu¸cão forte e fraca são equivalentes, ou seja se existir
uma prova de ∀n ∈ N P(n) por indu¸cão fraca então também existe uma prova por indu¸cão
forte. E vice-versa, se existir uma prova por indu¸cão forte então existe uma prova por indu¸cão
fraca.

Prova: É trivial que se existir uma prova dum dado resultado por indu¸cão fraca então
existe uma prova por indu¸cão forte, pois a mesma prova serve!
Portanto, resta-nos mostrar que se existir uma prova por indu¸cão forte então existe uma
prova por indu¸cão fraca. Para tal, vamos mostrar que se existe uma prova de ∀n ∈ Z+ P(n)
por indu¸cão forte, então existe uma prova por indu¸cão fraca de ∀n ∈ Z+ (∀i ≤ n P(i)).
Podemos depois concluir que existe uma prova por indu¸cão fraca de ∀n ∈ Z+ P(n) porque
(∀n ∈ Z+ (∀i ≤ n P(i))) ⇒ ∀n ∈ Z+ P(n).
Seja Q(n) a condi¸cão ∀i ≤ n P(i).
Mostrar que Q(1) é verdade, é mostrar que ∀i ≤ 1 P(i), o que equivale a mostrar que
P(1) é verdade. Como para mostrar que ∀n P(n) por indu¸cão forte, teve que se justificar
que P(1) era verdade, basta-nos reproduzir essa justifica¸cão.
Para mostrar que ∀n ( Q(n) ⇒ Q(n + 1) ), ou seja que
∀n ( (∀i ≤ n P(i)) ⇒ (∀i ≤ n + 1 P(i)) )
é útil recordar que existe uma prova de
∀n ( (∀i ≤ n P(i)) ⇒ P(n + 1) )
que teve de ser feita para mostrar a proposi¸cão ∀n P(n) por indu¸cão forte. E, como
∀n ((∀i ≤ n P(i)) ⇒ (∀i ≤ n P(i)))
tem-se ∀n ((∀i ≤ n P(i)) ⇒ (P(n+1)∧(∀i ≤ n P(i)))). Ou seja, ∀n ∈ Z+ (Q(n) ⇒ Q(n+1)).
Assim, mostrámos que Q(1) era verdade e ∀n ∈ Z+ (Q(n) ⇒ Q(n + 1)). Consequente-
mente, pelo princ´ıpio de indu¸cão fraca, concluimos ∀n ∈ Z+ Q(n).
4.2.1 Outras formula¸cões do princ´ıpio de indu¸cão
Proposi¸cão 17 Seja A = {n ∈ N | P(n)}, onde P(n) denota “n satisfaz a propriedade P”.
Se A satisfizer as condi¸cões (i) e (ii) seguintes, então A = N.
(i) 0 ∈ A
(ii) ∀k ∈ N (k ∈ A ⇒ k + 1 ∈ A)
Proposi¸cão 18 Seja A = {n ∈ N | P(n)}, onde P(n) denota “n satisfaz a propriedade P”.
Se A satisfizer as condi¸cões (i) e (ii) seguintes, então A = N.
(i) 0 ∈ A
(ii) ∀k∈N ( (∀i ≤ k i∈A) ⇒ k + 1 ∈ A )

Cap´ıtulo 5
Rela¸cões Binárias
5.1 Rela¸cões Binárias de A em B
Sejam A e B conjuntos. Designa-se por produto cartesiano de A por B, e denota-se por
A × B , o conjunto dos pares ordenados (a, b) tais que a ∈ A e b ∈ B , ou seja
A × B = {(a, b) | a ∈ A e b ∈ B}
Qualquer subconjunto R do produto cartesiano de A por B diz-se rela¸cão binária de A
em B. A nota¸cão a R b será usada com o mesmo significado de (a, b) ∈ R.
Exemplo 19 Seja A o conjunto dos alunos, P o conjunto dos docentes, L o conjunto das
licenciaturas e C o conjunto das disciplinas das licenciaturas da FCUP.
R = {(x, y) ∈ A × A | x e y são alunos da mesma licenciatura} ⊆ A × A
S = {(x, y) ∈ P × C | x é professor da disciplina y} ⊆ P × C
T = {(x, y) ∈ A × C | x está inscrito na disciplina y} ⊆ A × C
U = {(x, y) ∈ A × L | x é aluno da licenciatura y} ⊆ A × L
Os conjuntos R, S, T e U são rela¸cões binárias.
5.1.1 Opera¸cões com rela¸cões binárias
Como as rela¸cões binárias são conjuntos (de pares ordenados), podemos definir a união e a
interseçcão de rela¸cões binárias e ainda a rela¸cão complementar. Sendo R, S ⊆ A × B:
R ∪ S = {(a, b) ∈ A × B | (a, b) ∈ R ∨ (a, b) ∈ S}
R ∩ S = {(a, b) ∈ A × B | (a, b) ∈ R ∧ (a, b) ∈ S}
R = {(a, b) ∈ A × B | (a, b) /∈ R} = (A × B)R

5.1. RELAÇ ÕES BINÁRIAS DE A EM B 44
Para além destas opera¸cões, definimos também a no¸cão de inversa e de composta. A
rela¸cão inversa de R, representada por R−1, é a rela¸cão de B em A definida pelo conjunto
R−1
= {(b, a) | (a, b) ∈ R}
Dadas duas rela¸cões R ⊆ A × B e S ⊆ B × C, diz-se rela¸cão composta de R e S, e
representa-se por RS , a rela¸cão binária de A em C definida por
RS = {(a, c) | existe b ∈ B tal que (a, b) ∈ R e (b, c) ∈ S}
Em alternativa podiamos escrever S ◦ R, que se lê S após R, à semelhan¸ca da nota¸cão
usual para composi¸cão de fun¸cões. Na seçcão 5.1.3, veremos que as fun¸cões correspondem a
rela¸cões binárias que satisfazem condi¸cões adicionais. A rela¸cão inversa corresponde à no¸cão
de imagem rec´ıproca, que associa a cada transformado os elementos do dom´ınio que o têm
por imagem.
Exemplo 20 Seja A = {1, 2, 3}, B = {1, 2, 3, 4, 5}, C = {1, 2},
R = {(1, 2), (1, 3), (2, 2), (3, 4), (3, 5)}
S = {(1, 1), (3, 2), (5, 1), (5, 2)}
A rela¸cão R−1 é {(2, 1), (3, 1), (2, 2), (4, 3), (5, 3)}.
R S
1 GG
BB„„„„„„„„„„„„„„ 2
2
RRjjjjjjjjjjjjjj
3 GG 2
3
66ssssssssssssssss GG 5
BB„„„„„„„„„„„„„
SSjjjjjjjjjjjjj
1 GG 1
4
RS = {(1, 2), (3, 1), (3, 2)}, já que: (1, 2) ∈ RS pois (1, 3) ∈ R ∧ (3, 2) ∈ S; (3, 1) ∈ RS
porque (3, 5) ∈ R ∧ (5, 1) ∈ S; (3, 2) ∈ RS porque (3, 5) ∈ R ∧ (5, 2) ∈ S; (1, 1) /∈ RS porque
∀y ∈ B (1, y) /∈ R ∨ (y, 1) /∈ S (de facto, ∀y ∈ B (1, y) ∈ R ⇔ y = 2 ∨ y = 3, mas
(2, 1) /∈ S ∧ (3, 1) /∈ S); Do mesmo modo se verifica que, (2, 1) /∈ RS, (2, 2) /∈ RS.
Como RS ⊆ {1, 2, 3}×{1, 2}, o que acabámos de fazer foi uma análise exaustiva dos pares
poss´ıveis, justificando se pretenciam ou não a RS. Mais adiante, serão apresentados alguns
resultados teóricos que facilitarão a determina¸cão da composta.

Exemplo 21 Voltemos a considerar o Exemplo 19. Podemos verificar que:
{(x, y) ∈ A × P | x é aluno duma disciplina de que y é professor} = TS−1
R = {(x, y) ∈ A × A | x e y são alunos da mesma licenciatura } = UU −1
5.1.2 Matriz duma rela¸cão binária
Sejam A e B conjuntos finitos e não vazios, tais que |A| = n e |B| = m. Podemos identificar A
com {ai | 1 ≤ i ≤ n} e B com {bj | 1 ≤ j ≤ m}. Qualquer rela¸cão R de A em B pode
ser representada por uma tabela – matriz da rela¸cão – do modo seguinte. O elemento que
está na linha i e coluna j é 1 se (ai, bj) ∈ R, e é 0 se (ai, bj) /∈ R. Ou seja, se MR for tal
matriz, e MR[i, j] representar o elemento na linha i e coluna j então tem-se
MR[i, j] = 1 se e só se (ai, bj) ∈ R
MR[i, j] = 0 se e só se (ai, bj) /∈ R
com 1 ≤ i ≤ n e 1 ≤ j ≤ m.
Exemplo 22 Seja A = {1, 2, 3}, B = {1, 2, 3, 4, 5} e R ⊆ A × B,
R = {(1, 2), (1, 3), (2, 2), (3, 4), (3, 5)}
Então,
MR =



0 1 1 0 0
0 1 0 0 0
0 0 0 1 1



Matriz da inversa
Sejam A = {a1, . . . , an} e B = {b1, . . . , bm}, m, n ∈ Z+ (fixos) e R ⊆ A × B. Então
MR−1 [i, j] = 1 ⇐⇒ (bi, aj) ∈ R−1 ⇐⇒ (aj, bi) ∈ R ⇐⇒ MR[j, i] = 1
MR−1 [i, j] = 0 ⇐⇒ (bi, aj) /∈ R−1 ⇐⇒ (aj, bi) /∈ R ⇐⇒ MR[j, i] = 0
com 1 ≤ i ≤ m e 1 ≤ j ≤ n, pelo que a matriz da inversa de R é a transposta da matriz
de R (cada linha da transposta de R é uma coluna da matriz R).
Exemplo 23 Para R como no Exemplo 22, R−1 = {(2, 1), (3, 1), (2, 2), (4, 3), (5, 3)}. Então,
MR−1 =








0 0 0
1 1 0
1 0 0
0 0 1
0 0 1








=



0 1 1 0 0
0 1 0 0 0
0 0 0 1 1



t
= Mt
R

Matriz da composta
Sejam A, B, e C conjuntos finitos e não vazios tais que |A| = n, |B| = m e |C| = p. Dadas
duas rela¸cões R e S tais que R ⊆ A × B e S ⊆ B × C, a matriz da rela¸cão composta
RS tem n linhas e p colunas e
MRS[i, j] =
1≤k≤m
(MR[i, k] ∧ MS[k, j]), 1 ≤ i ≤ n, 1 ≤ j ≤ p
Notar que por defini¸cão da rela¸cão composta tem-se aiRScj se e só se existe bk tal que
aiRbk ∧ bkScj. Ou seja, MRS[i, j] = 1 se e só se MR[i, k] = 1 ∧ MS[k, j] = 1 para algum k.
Ou seja, MRS[i, j] = 1 se e só se MR[i, 1] = 1∧MS[1, j] = 1 ou MR[i, 2] = 1∧MS[2, j] = 1
ou . . . ou MR[i, m] = 1∧MS[m, j] = 1, o que justifica a defini¸cão dada para MRS[i, j]. Assim,
MRS = MRMS é um produto1 de matrizes cujos elementos pertencem ao corpo ({0, 1}, ∨, ∧).
Relembre que ∨ e ∧ denotam “ou” e “e” respectivamente e “0” e “1” representam os
valores lógicos falso e verdadeiro.
∨ 0 1
0 0 1
1 1 1
∧ 0 1
0 0 0
1 0 1
Exemplo 24 Seja A = {1, 2, 3}, B = {1, 2, 3, 4, 5}, C = {1, 2},
R = {(1, 2), (1, 3), (2, 2), (3, 4), (3, 5)}
MR =



0 1 1 0 0
0 1 0 0 0
0 0 0 1 1



S = {(1, 1), (3, 2), (5, 1), (5, 2)}
MS =








1 0
0 0
0 1
0 0
1 1








MRS =



0 1
0 0
1 1


 =



0 1 1 0 0
0 1 0 0 0
0 0 0 1 1











1 0
0 0
0 1
0 0
1 1








donde, RS = {(1, 2), (3, 1), (3, 2)} ⊆ A × C
1
Deve ficar claro quando estudar corpos e matrizes na disciplina de Elementos de Álgebra Linear. Para
matrizes cujos elementos pertencem ao corpo dos reais (R, +, ∗), se M tem n linhas e m colunas e N tem m
linhas e p colunas, a matriz MN tem n linhas e p colunas, sendo MN[i, j] =
Pm
k=1(A[i, k] ∗ B[k, j]), para
1 ≤ i ≤ n e 1 ≤ j ≤ p (dado pelo produto escalar da linha i de M pela coluna j de N). Quando os elementos
pertencem a ({0, 1}, ∨, ∧), a disjun¸cão ∨ substitui a soma + e a conjun¸cão ∧ substitui o produto ∗.

5.2. RELAÇ ÕES BINÁRIAS DEFINIDAS NUM CONJUNTO 47
5.1.3 Fun¸cões de A em B
Designa-se por fun¸cão de A em B qualquer rela¸cão binária f de A em B tal que para todo
a ∈ A existe um único b ∈ B tal que a f b, ou seja,
∀a ∈ A ∃1
b ∈ B a f b.
Se a f b então escreve-se f(a) = b e diz-se que b é a imagem de a por f.
O conjunto A é o dom´ınio da fun¸cão, e o conjunto B é o conjunto de chegada. O
subconjunto de B formado pelas imagens dos elementos de A diz-se imagem de A por f,
ou contradom´ınio de f. A imagem de A por f denota-se por f(A).
Uma fun¸cão é injectiva se e só se cada elemento de B é imagem quando muito dum
elemento de A, ou seja
f injectiva sse ∀a1, a2 ∈ A ( f(a1) = f(a2) ⇒ a1 = a2 )
Uma fun¸cão é sobrejectiva se e só qualquer elemento de B é imagem de algum elemento
de A, ou seja f(A) = B.
Uma fun¸cão que é sobrejectiva e injectiva diz-se bijectiva. Assim, f ⊆ A × B é uma
fun¸cão bijectiva se e só se
• ∀a ∈ A ∃1b ∈ B f(a) = b (fun¸cão), e
• ∀b ∈ B ∃1a ∈ A f(a) = b (bijectiva)
Desta observa¸cão resulta trivialmente a proposi¸cão seguinte.
Proposi¸cão 19 Seja f ⊆ A × B uma fun¸cão. Então f −1 ⊆ B × A é fun¸cão se e só se f é
bijectiva.
Uma fun¸cão diz-se invert´ıvel se a sua inversa é uma fun¸cão.
Uma fun¸cão parcial de A em B é uma rela¸cão binária f de A em B tal que se um elemento
a ∈ A tem imagem por f então essa imagem é única. Notar que a diferen¸ca relativamente
à defini¸cão de fun¸cão é não se impor a condi¸cão de que todos os elementos de A tenham
imagens por f.
5.2 Rela¸cões Binárias Definidas num Conjunto
Seja A um conjunto. Chama-se rela¸cão binária definida em A ou simplesmente rela¸cão
binária em A a qualquer rela¸cão binária de A em A.

5.2.1 Propriedades das rela¸cões binárias definidas em A
Qualquer rela¸cão R definida em A pode gozar ou não das propriedades seguintes.
reflexividade: R é reflexiva sse ∀x ∈ A xRx, ou seja não existe x tal que x ∈ A e (x, x) /∈ R.
simetria: R é simétrica sse ∀x, y ∈ A (xRy ⇒ yRx), ou seja não existem x, y tais que
x, y ∈ A e (x, y) ∈ R e (y, x) /∈ R.
antissimetria: R é antissimétrica sse ∀x, y ∈ A ((xRy∧yRx) ⇒ x = y), ou seja, não existem
x, y ∈ A tais que x = y, xRy e yRx.
transitividade: R é transitiva sse ∀x, y, z ∈ A (xRy ∧ yRz) ⇒ xRz, ou seja não existem
x, y, z tais que x, y, z ∈ A, xRy, yRz e (x, z) /∈ R.
Exemplo 25 Seja A = {1, 2, 3, 4, 5}, e α, β, γ, e φ rela¸cões binárias em A, assim definidas
α = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}
β = {(1, 1), (1, 3), (3, 1)}
γ = {(1, 1), (1, 3)}
φ = A × A
A rela¸cão α é reflexiva, simétrica, transitiva, e antissimétrica. De facto, uma vez que
α = {(x, x) | x ∈ A}, é claro que ∀x ∈ A (x, x) ∈ α, ou seja α é reflexiva. Por defini¸cão
de α tem-se
∀x, y ∈ A ( (x, y) ∈ α ⇒ x = y ). (5.1)
Donde, ∀x, y ∈ A ( (x, y) ∈ α ⇒ (y, x) ∈ α ) ou seja, α é simétrica. Do mesmo modo, por
(5.1) conclui-se ∀x, y, z ∈ A ( (x, y) ∈ α ∧ (y, z) ∈ α ⇒ (x, z) ∈ α ) ou seja α é transitiva.
E ainda, ∀x, y ∈ A ( (x, y) ∈ α ∧ (y, x) ∈ α ⇒ x = y ) ou seja, α é antissimétrica.
β não é reflexiva (porque por exemplo 5 ∈ A ∧ (5, 5) /∈ β), é simétrica (porque (1, 3) ∈ β
mas (3, 1) ∈ β), não antissimétrica (porque 1 = 3 ∧ (1, 3) ∈ β ∧ (3, 1) ∈ β), e não transitiva
(porque (3, 1) ∈ β ∧ (1, 3) ∈ β ∧ (3, 3) /∈ β).
γ é transitiva, antissimétrica, não reflexiva, e não simétrica (Justificar!).
φ é reflexiva, simétrica, transitiva e não antissimétrica.
5.2.2 Grafo da rela¸cão
As rela¸cões em A podem ser representadas por grafos dirigidos os quais são constitu´ıdos
por um conjunto de vértices (que representam os elementos de A) e um conjunto de ramos
(que correspondem aos pares ordenados que pertencem à rela¸cão).

Exemplo 26 Para as rela¸cões consideradas no Exemplo 25:
O grafo da rela¸cão α:
1•
GFEDBCoo 2•
GFEDBCoo 3•
GFEDBCoo 4•
GFEDBCoo 5•
GFEDBCoo
O grafo da rela¸cão β:
1•
BC@AGFGG GG
3•oo 4• 5• 2•
Exemplo 27 Seja R a seguinte rela¸cão definida em Z+ por
R = {(x, y) | y ≤ 9, y é múltiplo de x, y = x} ∪ {(1, 1)}
• R em extensão
R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7),
(1, 8), (2, 4), (2, 6), (2, 8), (3, 6), (3, 9), (4, 8)}
• o grafo de R
1•
@AGFED
}}|||||||||||||||||||
ÖÖ
@@
$$IIIIIIIIIIIIIII
77vvvvvvvvvvvvvvvvvvvvvvvvv
BB……………………………………………………………
CCˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆ
2•
}}||||||||
33ffffffff
vvmmmmmmmmmmmmmmm 3•
}}||||||||
33ffffffff •5 •7
•8 •4oo •6 •9
• a matriz de R 

















1 1 1 1 1 1 1 1 1
0 0 0 1 0 1 0 1 0
0 0 0 0 0 1 0 0 1
0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0



















5.3. RELAÇ ÕES DE COMPATIBILIDADE E DE EQUIVALÊNCIA 50
Exemplo 28 Seja A o conjunto dos alunos da FCUP. Sejam R, S ⊆ A × A as rela¸cões
binárias em A assim definidas
R = {(x, y) ∈ A × A | x e y são alunos da mesma licenciatura da FCUP}
S = {(x, y) ∈ A × A | x e y estão inscritos numa mesma disciplina}
R é reflexiva porque qualquer aluno da FCUP é aluno da mesmo curso que si próprio. É
simétrica porque se um aluno x da FCUP frequenta o mesmo curso que um aluno y, então y
frequenta o mesmo curso que x. Não é antissimétrica, já que se o fosse cada licenciatura da
FCUP seria frequentada quando muito por um aluno (o que é trivialmente falso). É transitiva
porque se um aluno x frequenta o mesmo curso que um aluno y, e y frequenta o mesmo curso
que z, então x e z frequentam o mesmo curso, já que cada aluno está inscrito num e num só
curso.
S é reflexiva, simétrica, não antissimétrica, e não transitiva (alunos de cursos/anos dife-
rentes podem partilhar disciplinas, pelo que existem alunos x, y e z tais que x e y frequentam
uma mesma disciplina, e y e z frequentam uma mesma disciplina, e x e z não têm qualquer
disciplina em comum).
5.3 Rela¸cões de Compatibilidade e de Equivalência
Diz-se rela¸cão de compatibilidade em A toda rela¸cão binária em A que é reflexiva e
simétrica. Qualquer rela¸cão de compatibilidade em A que seja ainda transitiva diz-se rela¸cão
de equivalência em A (ou seja, é uma rela¸cão reflexiva, simétrica, e transitiva).
Exemplo 29 Considere o Exemplo 28. Como R e S são reflexivas e simétricas, R e S são
rela¸cões de compatibilidade. R é reflexiva, simétrica e transitiva, pelo que é de equivalência.
S não é de equivalência porque não é transitiva.
Se γ uma rela¸cão de compatibilidade em A e x ∈ A e y ∈ A, diz-se que x e y são elementos
compat´ıveis para γ se e só se xγy. Se (x, y) /∈ γ então x e y dizem-se incompat´ıveis
para γ. Analogamente, se γ é uma rela¸cão de equivalência em A e xγy, então x e y dizem-se
equivalentes (para γ).
Seja γ uma qualquer rela¸cão de compatibilidade em A. Seja x um elemento qualquer de A
e considere-se o conjunto Cx de todos os elementos de A compat´ıveis com x (para γ), ou seja
Cx = {y ∈ A | (x, y) ∈ γ}.

Exemplo 30 Para A = {1, 2, 3, 4} e γ = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (2, 3), (2, 1), (3, 2)}
tem-se:
C1 = {1, 2} C2 = {1, 2, 3}
C3 = {2, 3} C4 = {4}
Repare-se que C2 tem elementos incompat´ıveis, já que (1, 3) /∈ γ. A rela¸cão γ é de compati-
bilidade mas não é de equivalência.
5.3.1 Classes de equivalência
Pode acontecer, para certas rela¸cões de compatibilidade γ, que existam elementos u e v em
Cx que sejam incompat´ıveis. No entanto, pode-se mostrar a proposi¸cão seguinte:
Proposi¸cão 20 Seja γ uma rela¸cão de compatibilidade em A. A rela¸cão γ é de equivalência
se e só se para todo x ∈ A, o conjunto Cx = {y ∈ A | (x, y) ∈ γ} não tem elementos
incompat´ıveis.
Prova: Seja γ de compatibilidade em A. Vamos mostrar que
γ transitiva ⇒ ∀x ∈ A ∀y, t ∈ Cx yγt.
Por defini¸cão de Cx, se y, t ∈ Cx então xγt e xγy. Como γ é simétrica, se xγy também yγx.
Então, se xγt e xγy, também yγx e xγt. Logo, pela transitividade de γ, deduz-se yγt.
Reciprocamente, se se verificar (5.2)
∀x ∈ A ∀y, t ∈ Cx yγt (5.2)
então γ é transitiva. De facto, se a, b, c ∈ A são tais que aγb e bγc então, pela simetria de γ
e por defini¸cão de Cb, deduz-se c ∈ Cb e a ∈ Cb. Mas por (5.2), (c ∈ Cb ∧ a ∈ Cb) ⇒ aγc.
Então ∀a, b, c ∈ A ((aγb ∧ bγc) ⇒ aγc), ou seja γ é transitiva.
Sendo γ de equivalência em A, cada conjunto Cx chama-se classe de equivalência de γ.
Concretamante, será a classe de equivalência do elemnto x, ou seja, o conjunto dos elementos
de A que são equivalentes a x (em γ).
Proposi¸cão 21 Se γ é uma rela¸cão de equivalência em A então cada elemento de A pertence
a uma e uma só classe de equivalência de γ.
Qualquer elemento de uma classe de equivalência pode ser usado para identificar a
classe.

Exemplo 31 Seja A = {x | x é aluno da FCUP}, e
R = {(x, y) ∈ A × A | x e y são alunos da mesma licenciatura}
que como vimos é de equivalência. Eis algumas das classes de equivalência de R (actualmente
existem 19 classes):
{x ∈ A | x é aluno de Matemática}
{x ∈ A | x é aluno de Geologia}
{x ∈ A | x é aluno de Ciência de Computadores}
{x ∈ A | x é aluno de Engenharia de Redes e Sistemas Informáticos}
{x ∈ A | x é aluno de Bioqu´ımica}
{x ∈ A | x é aluno de Engenharia das Ciências Agrárias}
{x ∈ A | x é aluno de Matemática Aplicada à Tecnologia}
Exemplo 32 Seja ≡5 a rela¸cão definida no conjunto dos inteiros por
x ≡5 y sse x − y é múltiplo (inteiro) de 5
quaisquer que sejam x, y ∈ Z.
≡5 é reflexiva porque qualquer que seja x ∈ Z tem-se x − x = 0 = 0 × 5. É simétrica
porque para quaisquer x, y ∈ Z tem-se
x ≡5 y ⇐⇒ (∃k ∈ Z x − y = 5k) ⇐⇒ (∃k ∈ Z y − x = 5k )
(toma-se k = −k). Logo, ∀x, y ∈ Z ( x ≡5 y ⇒ y ≡5 x), ou seja ≡5é simétrica. Mostrar
que ≡5 é transitiva é mostrar que ∀x, y, z ∈ Z [ (x ≡5 y ∧ y ≡5 z) ⇒ x ≡5 z ]. Se
x ≡5 y ∧ y ≡5 z então existem k, k ∈ Z tais que x − y = 5k ∧ y − z = 5k . Assim,
x − z = (x − y) + (y − z) = 5(k + k ). Logo, x ≡5 z.
São 5 as classes de equivalência de ≡5, a saber:
C0 = {x ∈ Z | 0 ≡5 x} = {x ∈ Z | ∃k ∈ Z x = 5k}
C1 = {x ∈ Z | 1 ≡5 x} = {x ∈ Z | ∃k ∈ Z x = 5k + 1}
C2 = {x ∈ Z | ∃k ∈ Z x = 5k + 2}
C3 = {x ∈ Z | ∃k ∈ Z x = 5k + 3}
C4 = {x ∈ Z | ∃k ∈ Z x = 5k + 4}
A rela¸cão podia também ser definida assim
x ≡5 y sse são iguais os restos da divisão inteira de x e y por 5
A nota¸cão mais habitual é x ≡ y (mod 5).

Proposi¸cão 22 (Caracteriza¸cão das classes de equivalência) Seja γ de equivalência
em A, conjunto não vazio. Para cada x ∈ A, seja Cx = {y ∈ A | xγy}. Então,
(i) qualquer que seja a ∈ A, o conjunto Ca é não vazio.
(ii) se Ca ∩ Cb = ∅ então Ca = Cb.
(iii) o conjunto A é a união dos conjuntos Ca, com a ∈ A.
Prova:
(i) ∀a ∈ A aγa, pela reflexividade de γ. Assim, ∀a ∈ A a ∈ Ca. Logo, Ca = ∅.
(ii) Vamos agora mostrar que se Ca ∩ Cb = ∅ então Ca ⊆ Cb, e Ca ⊇ Cb, pelo que Ca = Cb.
Como Ca ∩ Cb = ∅, existe c ∈ A tal que c ∈ Ca ∩ Cb. Seja x um qualquer elemento de
Ca. Vamos mostrar que x ∈ Cb. Para isso basta mostrar que xγb. Ora, pela Proposi¸cão
20, (x ∈ Ca ∧ c ∈ Ca) ⇒ xγc. E como cγb (pois c ∈ Cb), conclui-se por transitividade
que xγb. Donde Ca ⊆ Cb. De modo análogo se verifica que x ∈ Cb ⇒ x ∈ Ca
(iii) A ⊇ a∈A Ca, já que Ca ⊆ A para todo a ∈ A. Por outro lado, verificou-se em (i) que
para todo a ∈ A, a ∈ Ca. Pelo que A ⊆ a∈A Ca.
Exerc´ıcio 5.3.1 Considere a rela¸cão θ em Z × Z+ assim definida:
(p, q) θ (p , q ) sse pq = qp .
Verificar que θ é de equivalência. Notar que cada classe de equivalência de θ corresponde a
um e um só racional no sentido seguinte: C(p,q) = {(x, y) ∈ Z × Z+ | x/y = p/q}.
5.3.2 Parti¸cões e rela¸cões de equivalência
Designa-se por parti¸cão de A um conjunto de subconjuntos de A que são não vazios, disjuntos
dois a dois, e cuja união é o conjunto A.
Exemplo 33 Para A = {1, 2, 3, 4}, o conjunto P1 = {{1, 2}, {3}, {4}} define uma parti¸cão de
A mas P2 = {{1, 2}, {3, 2}, {4}} não, já que {1, 2} ∩ {3, 2} = ∅. Também, P3 = {{1, 2}, {3}}
não define parti¸cão de A já que 4 ∈ A e 4 não pertence a nenhum dos subconjuntos de A que
constituem P3.

Corolário 22.1 Se γ é uma rela¸cão de equivalência em A então o conjunto das classes de
equivalência de γ é uma parti¸cão do conjunto A.
O conjunto das classes de equivalência de uma rela¸cão de equivalência γ definida em A
diz-se conjunto quociente de A por γ, e representa-se por A/γ.
Exemplo 34 Para ≡5, definida no Exemplo 32, o conjunto quociente é:
Z/≡5 = {C0, C1, C2, C3, C4}.
Proposi¸cão 23 Seja A um conjunto não vazio e seja Π uma parti¸cão de A. Existe uma e
uma só rela¸cão γ de equivalência em A tal que A/γ = Π. Essa rela¸cão γ é
{(x, y) ∈ A × A | x e y pertencem a um mesmo elemento de Π}
Prova: Seja θ a rela¸cão definida em A tal que
θ = {(x, y) ∈ A × A | x e y pertencem a um mesmo elemento de Π}
Vamos mostrar que θ é rela¸cão de equivalência em A.
A rela¸cão θ é reflexiva, porque sendo Π uma parti¸cão de A, todo elemento de a ∈ A
pertence a algum subconjunto em Π, pelo que ∀a ∈ A aθa. Mostrar que θ é simétrica, é
mostrar que
∀a, b ∈ A ( aθb ⇒ bθa),
o que segue trivialmente da defini¸cão de θ. É transitiva porque quaisquer que sejam a, b, c ∈ A,
se a e b são elementos dum mesmo conjunto em Π, e b e c são elementos dum mesmo conjunto
em Π, então esses conjuntos são iguais (uma vez que os elementos de Π são disjuntos dois a
dois). Logo, se aθb e bθc então aθc. Concluimos assim que θ é de equivalência.
Vamos mostrar que A/θ = Π. Seja x ∈ A, e Cx a classe de equivalência de x para θ.
Seja Px ∈ Π tal que x ∈ Px. Vamos mostrar que Cx = Px. Por defini¸cão de θ, é claro que
Px ⊆ Cx. Por outro lado, se Cx ⊆ Px então existiria y ∈ Cx tal que y /∈ Px. Mas, y ∈ Cx
sse yθx, ou seja sse y e x pertencem a um mesmo conjunto em Π. Então existiria P = Px,
P ∈ Π tal que x ∈ Px ∩ P , o que é absurdo, pois Px e P são elementos duma parti¸cão,
P = Px, sendo por isso disjuntos. Logo, também Cx ⊆ Px. Cada conjunto em A/θ (assim
como cada conjunto em Π) fica perfeitamente identificado com a indica¸cão dum elemento x
que lhe perten¸ca. Consequentemente, acabámos de mostrar que A/θ = Π.

Seja γ uma rela¸cão de equivalência em A tal que A/γ = Π. Já vimos que uma tal rela¸cão
existe sempre, já que θ é um exemplo. Vamos mostrar agora que existe uma só rela¸cão nessas
condi¸cões, ou seja
∀γ ⊆ A × A [ ( γ de equivalência ∧ A/γ = Π ) ⇒ γ = θ
Como rela¸cões binárias são, por defini¸cão, conjuntos, para mostrar que γ = θ, vamos
mostrar que γ ⊆ θ ∧ γ ⊇ θ.
Sejam x e y elementos de A. Se (x, y) ∈ γ então, por defini¸cão de conjunto quociente
A/γ, existe um e um só subconjunto em Π, seja Cx tal que x, y ∈ Cx. Mas, por defini¸cão de
θ, tem-se x, y ∈ Cx ∈ Π sse (x, y) ∈ θ. Logo γ ⊆ θ.
Verifiquemos agora que θ ⊆ γ. Se (x, y) ∈ θ então existe P ∈ Π tal que x, y ∈ P. Como
Π é o conjunto das classes de equivalência de γ, se x, y ∈ P então xγy.
5.3.3 Classes de Compatibilidade
Se γ é de compatibilidade em A podemos considerar subconjuntos de A, não vazios, e que não
tenham elementos incompat´ıveis. Ou seja, subconjuntos C de A que satisfa¸cam as condi¸cões
(i) e (ii) seguintes:
(i) C = ∅
(ii) quaisquer que sejam a e b pertencentes a C tem-se aγb.
Um tal conjunto C designa-se por classe de compatibilidade de γ. Algumas classes de
compatibilidade de γ podem estar contidas propriamente noutras classes de compatibilidade
de γ. Diz-se classe máxima de compatibilidade de γ qualquer classe de compatibilidade
de γ que não está contida propriamente noutra classe de compatibilidade de γ. Assim, C ⊆ A
é classe máxima de compatibilidade se e só se C satisfaz as condi¸cões (i) e (ii) anteriores e
ainda (iii):
(i) C = ∅
(ii) ∀a,b∈C aγb.
(iii) Se C é uma classe de compatibilidade γ tal que C ⊆ C , então C = C .
Exemplo 35 Seja O = {o1, o2, o3, o4, o5, o6, o7} um conjunto de objectos, e seja
R = { (o1, {verde, amarelo}), (o2, {azul, verde}), (o3, {azul, vermelho}), (o5, {branco}),
(o4, {verde, castanho}), (o6, {branco, castanho, amarelo}), (o7, {preto})}

uma fun¸cão do conjunto O no conjunto dos subconjuntos das cores, que indica quais as cores
de cada objecto. A rela¸cão γ definida em O por
xγy sse x e y têm uma cor em comum
é de compatibilidade. As classes de compatibilidade de γ são:
{o1} {o2} {o3} {o4} {o5} {o6} {o7}
{o1, o2} {o1, o4} {o1, o6} {o2, o3} {o4, o6} {o5, o6}
{o1, o2, o4} {o1, o4, o6}
As classes de máxima compatibilidade são:
{o1, o2, o4}, {o1, o4, o6}, {o2, o3}, {o5, o6}, {o7}
Exerc´ıcio 5.3.2 Mostrar que:
a) Se γ é de equivalência em A então para todo x ∈ A, a classe de equivalência de x é uma
classe de compatibilidade de γ.
b) Se γ é de compatibilidade em A então todo x ∈ A pertence a alguma classe máxima de
compatibilidade de γ.
c) Se γ é uma rela¸cão de compatibilidade em A, então a união das classes máximas de
compatibilidade de γ é o conjunto A.
d) Se γ é de equivalência em A, então o conjunto das classes máximas de compatibilidade
de γ é o conjunto quociente A/γ.
e) Se γ é de compatibilidade em A e Cγ(A) é o conjunto das classes máximas de compati-
bilidade de γ, então γ = θθ−1 em que θ ⊆ A × Cγ(A) é assim definida
xθC sse x ∈ C,
quaisquer que sejam x ∈ A, e C ∈ Cγ(A).

5.4. RELAÇ ÕES DE ORDEM PARCIAL 57
5.4 Rela¸cões de Ordem Parcial
Uma rela¸cão de ordem parcial definida num conjunto A é uma rela¸cão binária reflexiva,
antissimétrica e transitiva.
A rela¸cão ≤ definida nos conjunto dos números reais por
x ≤ y sse ∃r ∈ R+
0 y = x + r
é de ordem parcial em R porque:
• ≤ é reflexiva porque ∀x ∈ R x = x + 0, pelo que ∀x ∈ R x ≤ x.
• ≤ é antissimétrica porque quaisquer que sejam x, y ∈ R se x ≤ y e y ≤ x então existem
z1, z2 ∈ R+
0 tais que y = x + z1 e x = y + z2. Logo, x = (x + z1) + z2, pelo que
z1 + z2 = 0. Mas como z1, z2 ∈ R+
0 , vem z1 = z2 = 0, pelo que x = y. Assim,
∀x, y ∈ R ((xRy ∧ yRx) ⇒ x = y), ou seja R é antissimétrica.
• ≤ é transitiva porque quaisquer que sejam x, y, z ∈ R se x ≤ y e y ≤ z então existem
z1, z2 ∈ R+
0 tais que y = x + z1 e z = y + z2. Logo, z = (x + z1) + z2 = x + (z1 + z2),
com z1 + z2 ∈ R+
0 , concluindo-se que x ≤ z (pela defini¸cão).
A sua inversa ≤−1, que se denota por ≥, é também de ordem parcial em R. O prolonga-
mento natural de ≤ a Rn assim definido
(x1, . . . , xn) ≤n (y1, . . . , yn) sse ∀1 ≤ i ≤ n xi ≤ yi
é também de ordem parcial.
Mais alguns exemplos:
• A ordem lexicográfica em Rn definida por
(x1, . . . , xn) ≤lex (y1, . . . , yn) sse (∀i xi = yi) ou (k = min{i | xi = yi} ∧ xk ≤ yk)
A ordem do dicionário (de Português) é um exemplo duma “ordem lexicográfica” no
conjunto das palavras de alfabeto {a, b, c, . . . , z} ∪ {−}.
• A rela¸cão definida nos inteiros positivos pelos pares (m, n) tais que n é múltiplo de m
também é de ordem parcial em Z+.
• Qualquer que seja o conjunto A, a rela¸cão de inclusão ⊆ em 2A (conjunto dos subcon-
juntos de A) é de ordem parcial. A rela¸cão inversa é ⊇, também é de ordem parcial.

É usual representar as rela¸cões de ordem parcial por . Um conjunto parcialmente
ordenado é um par (A, ) em que A é um conjunto e uma rela¸cão de ordem parcial
em A. Um conjunto parcialmente ordenado (A, ) diz-se conjunto totalmente ordenado
sse quaisquer que sejam x e y de A se tem x y ou y x.
Exemplo 36 (R, ≤) é totalmente ordenado, já que ∀x, y ∈ R ( x ≤ y ∨ y ≤ x).
(Z+, |) não é totalmente ordenado, sendo | a rela¸cão “divide”. Recorde que:
m|n sse ∃p ∈ Z+
n = mp
ou seja m|n sse n é múltiplo de m. De facto, existem x, y ∈ Z+ tais que x não divide y nem
y divide x. Por exemplo, (2, 3) /∈ |, e (3, 2) /∈ |.
Seja D = {x ∈ Z+ | x divide 64}. Então a restri¸cão de | a D é uma ordem total, ou seja
(D, |) é totalmente ordenado.
(2A, ⊆) não é totalmente ordenado, se A tiver pelo menos dois elementos. Por exemplo,
A = {1, 2}, 2A = {∅, {1}, {2}, A}, e {2} ⊆ {1} e {1} ⊆ {2}.
(Rn, ≤lex) é totalmente ordenado. Mas, (Rn, ≤n), para n ≥ 2 (fixo), não está totalmente
ordenado.
Exerc´ıcio 5.4.1 Mostrar que se R é de ordem parcial (total) em A então R−1 também é de
ordem parcial (total) em A.
5.4.1 Diagrama de Hasse
Uma rela¸cão de ordem parcial definida num conjunto finito, representa-se graficamente por
um Diagrama de Hasse. É um grafo não dirigido que se obtem por simplifica¸cão do grafo
da rela¸cão removendo todos os lacetes e todos os ramos que podem ser deduzidos pela transiti-
vidade da rela¸cão. Convenciona-se ainda que se um elemento precede (na rela¸cão definida)
um outro elemento, então o vértice do primeiro ficará situado mais abaixo na figura, e por
isso pode-se substituir “setas” (ramos orientados) por “segmentos” (ramos não orientados).
Exemplo 37 À esquerda apresenta-se o diagrama de Hasse da restri¸cão da rela¸cão divide
ao conjunto dos divisores de 16. À direita encontra-se o diagrama de Hasse para a restri¸cão
da mesma rela¸cão ao conjunto dos divisores de 30.

16
8
4
2
1
30
oooooo
€€€€€€
6
yyyyyy 10
oooooo
€€€€€€ 15
nnnnnn
2
yyyyyy 3 5
nnnnnnn
1
Exemplo 38 O diagrama de Hasse seguinte representa o conjunto parcialmente ordenado
(A, ⊆) para A = {∅, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {2, 3}, {2, 4}, {3, 4}, {2, 3, 4}}.
{1, 2}
bbbbbbbbbbbb
{1, 3}
bbbbbbbbbbbb
ÐÐÐÐÐÐÐÐÐÐÐÐ
{2, 3, 4}
nnnnnnn
€€€€€€€
{2, 3}
ooooooo
{3, 4}
nnnnnnnn
{2, 4}
ddddddddddddddddddddddddddddddd
nnnnnnnn
{1}
‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡ {2}
yyyyyyyyy {3} {4}
mmmmmmmmmm
∅
Os elementos {1, 2}, {1, 3} e {2, 3, 4} dizem-se elementos maximais. O elemento ∅ diz-se
m´ınimo.
O conjunto parcialmente ordenado ( (A ∪ {{1, 2, 3, 4}}) {∅}, ⊆ ) não tem m´ınimo, mas
tem máximo. Os elementos {1}, {2}, {3} e {4} são elementos minimais.
{1, 2, 3, 4}
ˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆ
mmmmmmm
{1, 2}
ggggggggggggg
{1, 3}
ggggggggggggg
{{{{{{{{{{{{{
{2, 3, 4}
nnnnnnn
€€€€€€€
{2, 3}
mmmmmmmmm
{3, 4}
nnnnnnnn
{2, 4}
dddddddddddddddddddddddddddddddddd
nnnnnnnn
{1} {2} {3} {4}
5.4.2 Máximos, m´ınimos, supremo, ´ınfimo, majorantes e minorantes
Seja uma rela¸cão de ordem parcial em A e seja S um subconjunto de A:
• m ∈ A é majorante de S sse ∀a ∈ S a m;
• m ∈ A é minorante de S sse ∀a ∈ S m a

5.5. FECHOS DUMA RELAÇ ÃO PARA UMA PROPRIEDADE 60
• s ∈ A é supremo de S sse s é majorante de S e para qualquer s majorante de S temos
s s . Se s ∈ S, então s designa-se por máximo de S.
• i ∈ A é ´ınfimo de S sse i é minorante de S e para qualquer i minorante de S temos
i i. Se s ∈ S, então s designa-se por m´ınimo de S.
• m ∈ S é elemento maximal de S se não existe s ∈ S tal que s = s e s s .
• m ∈ S é elemento minimal de S se não existe s ∈ S tal que s = s e s s.
Um conjunto parcialmente ordenado (A, ) diz-se reticulado se quaisquer que sejam
x, y ∈ A, o conjunto {x}∪{y} tem supremo e ´ınfimo. Para referir o supremo (resp., o ´ınfimo)
de {x} ∪ {y} escrevemos sup(x, y) (respectivamente inf(x, y)).
Exemplo 39 Os conjuntos parcialmente ordenados representados pelos diagramas de Hasse
seguintes são reticulados.
16
8
4
2
1
{1, 2, 3}
nnnnnnn
€€€€€€€
{1, 2}
€€€€€€€€ {1, 3}
nnnnnnnn
€€€€€€€€ {2, 3}
nnnnnnnn
{1}
{2} {3}
mmmmmmmmmm
∅
O conjunto parcialmente ordenado (Z+, |) é um reticulado, sendo | a rela¸cão “divide”.
Neste caso, sup(x, y) = mmc(x, y) e inf(x, y) = mdc(x, y), quaisquer que sejam x, y ∈ Z+
(mmc designa o m´ınimo múltiplo comum e mdc o máximo divisor comum).
(2A, ⊆) é um reticulado. Neste caso, sup(X, Y ) = X ∪Y e inf(X, Y ) = X ∩Y , quaisquer
que sejam X, Y ∈ 2A.
5.5 Fechos duma Rela¸cão para uma Propriedade
Seja R uma rela¸cão binária em A. Se existir alguma rela¸cão binária em A que contenha R
e goze da propriedade P, então a menor (no sentido da inclusão de conjuntos) das rela¸cões
satisfazendo tal condi¸cão designa-se por fecho da rela¸cão R para a propriedade P. Ou
seja, se RP for o fecho da rela¸cão R para a propriedade P então
(i) R ⊆ RP ⊆ A × A, e
(ii) toda rela¸cão S ⊆ A × A que goze da propriedade P e contenha R, contém também RP .

Por exemplo, se Rsim denotar o fecho simétrico de R então
• R ⊆ Rsim ⊆ A × A, e
• ∀S ⊆ A × A ((R ⊆ S ∧ S simétrica) ⇒ S ⊇ Rsim), ou seja, qualquer rela¸cão S definida
em A que seja simétrica e contenha R, contém também Rsim.
Exemplo 40 Seja A = {1, 2, 3, 4, 5} e sejam θ e β rela¸cões binárias em A e assim definidas:
θ = {(1, 1), (2, 2), (3, 3), (1, 2)}
β = {(1, 1), (1, 2), (2, 1), (4, 1)}
O grafo de θ:
1•
@AGFED
GG 2•
GFEDBCoo 3•
GFEDBCoo •4 •5
O grafo de β:
•1
@AGFED
GG •2
oo
•3 •5
•4
yy
O fecho reflexivo de θ é θ ∪ {(4, 4), (5, 5)}. O fecho simétrico θ ∪ {(2, 1)}, e o fecho
transitivo é θ porque θ é transitiva.
O grafo do fecho reflexivo de θ:
•1
@AGFED
GG •2
GFEDBCoo •3
GFEDBCoo •4
GFEDBCoo •5
GFEDBCoo
O grafo do fecho simétrico de θ:
•1
@AGFED
GG •2
oo
GFEDBCoo •3
GFEDBCoo •4 •5
O fecho reflexivo de β é β ∪ {(2, 2), (3, 3), (4, 4), (5, 5)}. O fecho simétrico β ∪ {(1, 4)} e
o transitivo é β ∪ {(2, 2), (4, 2)}.
O grafo do fecho reflexivo de β:
•1
@AGFED
GG •2
oo
GFEDBCoo •3
BCEDGF
•5
BCEDGF
•4
yy
GF@ABCyy

O grafo do fecho simétrico de β:
•1
@AGFED

GG •2
oo
•3 •5
•4
yy
O grafo do fecho transitivo de β:
•1
@AGFED
GG •2
oo
GFEDBCoo •3 •5
•4
yy aa||||||||
O fecho simétrico e transitivo de β é β ∪ {(2, 2), (4, 2), (1, 4), (2, 4), (4, 4)}.
•1
@AGFED

GG •2
oo
}}||||||||
GFEDBCoo •3 •5
•4
yy aa||||||||
GF@ABCyy
Não faz sentido falar em fecho antissimétrico. Se uma rela¸cão não é antissimétrica,
então qualquer rela¸cão que a contenha também não é antissimétrica.
5.5.1 Fecho transitivo e percursos em grafos
Dada uma rela¸cão R ⊆ A × A, define-se, para cada i ∈ Z+, a rela¸cão Ri do modo seguinte:
R1 = R
Ri = RRi−1, i ≥ 2 (composta de R e Ri−1)
Proposi¸cão 24 Uma rela¸cão binária R definida em A é transitiva se e só se R2 ⊆ R.
Prova: Se R2 ⊆ R então existiam x, y ∈ A tais que (x, y) ∈ R2 e (x, y) /∈ R. Por
defini¸cão R2 = RR, donde xR2y se e só se existe z ∈ A tal que xRz e zRy. Ou seja,
∃x, y, z ∈ A (x, z) ∈ R ∧ (z, y) ∈ R ∧ (x, y) /∈ R, pelo que R não seria transitiva. Logo, se R
é transitiva então R2 ⊆ R.
A prova do rec´ıproco, deduz-se trivialmente do Corolário 25.1, o qual só será demonstrado
à frente. De facto, desse Corolário, podemos concluir que se R2 ⊆ R então R+ = R. Assim,
como R+ (fecho transitivo de R) é transitiva, R é transitiva.

Se A for finito, podemos desenhar o grafo de R. Dados dois vértices u, v ∈ A, chama-se
percurso de u para v no grafo a qualquer sequência finita formada por um ou mais ramos do
grafo, tal que o extremo final de qualquer ramo da sequência coincide com o extremo inicial
do ramo seguinte na sequência. O comprimento do percurso é número de arcos no percurso.
Dizer que uRiv equivale a dizer que existe um percurso com i ramos de u para v no grafo
de R, como se deduz do Lema 3. Vamos mostrar mais adiante que o fecho transitivo de R,
que se denota por R+, é dado por ∪i∈Z+ Ri, concluindo-se que uR+v se e só se existir um
percurso de u para v no grafo de R.
Lema 3 Seja R uma rela¸cão definida em A. Para quaisquer elementos x e y de A, e qualquer
inteiro positivo k tem-se xRk+1y se e só se existem k elementos de A, sejam x1, . . . xk, tais
que xRx1 ∧ . . . ∧ xiRxi+1 ∧ . . . ∧ xkRy.
Prova: Mostremos, por indu¸cão sobre k, que para todo k ∈ Z+ e quaisquer x, y ∈ A
xRk+1
y sse ∃x1, . . . , xk ∈ A (xRx1 ∧ . . . ∧ xkRy) (5.3)
Mostrar que (5.3) é válida para k = 1, equivale a mostrar que xR2y se e só se existe x1
tal que xRx1 ∧ x1Ry, o que é trivialmente válido por defini¸cão de R2.
Provemos agora que se (5.3) é válida para um dado k ∈ Z+ então é válida para k + 1.
Sejam x, y ∈ A tais que xR(k+1)+1y. Então, usando a defini¸cão de R(k+1)+1, vem
xR(k+1)+1
y sse ∃z ∈ A xRz ∧ zRk+1
y
Mas, por hipótese de indu¸cão,
zRk+1
y sse ∃y1 . . . yk ∈ A (zRy1 ∧ . . . ∧ ykRy)
Assim,
xR(k+1)+1
y sse ∃z, y1 . . . yk ∈ A (xRz ∧ zRy1 ∧ . . . ∧ ykRy)
Se fizermos x1 = z, x2 = y1, . . . , xk+1 = yk vem
xR(k+1)+1
y sse ∃x1, x2 . . . xk+1 ∈ A (xRx1 ∧ x1Rx2 ∧ . . . ∧ xk+1Ry).
Logo, mostrámos que (5.3) está nas condi¸cões do princ´ıpio de indu¸cão. Logo, por tal princ´ıpio,
(5.3) é válida para todo k ∈ Z+.

Exemplo 41 Seja R a rela¸cão binária em {1, 2, 3, 4, 5, 6, 7} representada pelo grafo seguinte.
1• GG 2•

GG 5• GG 6•
oo

4•
yy
3•oo 7•
yy
Tem-se:
• (1, 4) ∈ R3 pois (1, 2) ∈ R ∧ (2, 3) ∈ R ∧ (3, 4) ∈ R.
• (1, 1) ∈ R4 pois (1, 4) ∈ R3 ∧ (4, 1) ∈ R.
• (3, 3) ∈ R4 pois 3 R 4 ∧ 4 R 1 ∧ 1 R 2 ∧ 2 R 3.
• (5, 5) ∈ R+ pois (5, 5) ∈ R2 já que 5 R 6 ∧ 6 R 5.
• Como 3 R 4 ∧ 4 R 1 ∧ 1 R 2 ∧ 2 R 5 ∧ 5 R 6 ∧ 6 R 7, tem-se (3, 7) ∈ R6 ⊆ R+.
MR+ =













1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
0 0 0 0 1 1 1
0 0 0 0 1 1 1
0 0 0 0 1 1 1













A sequência de ramos (3, 4), (4, 1), (1, 2), (2, 5), (5, 6), (6, 7) é um percurso de 3 para 7.
Exerc´ıcio 5.5.1 Seja H = {x | x é ser humano} e sejam m~ae e pai rela¸cões binárias
definidas em H por:
(x, y) ∈ m~ae sse x é mãe de y
(x, y) ∈ pai sse x é pai de y
Qual é a composta de m~ae com pai? Qual é a composta de pai com m~ae? Qual é a composta
de pai ∪ m~ae com pai ∪ m~ae? Qual é o fecho transitivo de pai ∪ m~ae? Qual é a inversa de
(pai ∪ m~ae)+?
Resposta: x é avó paterna de y, x é avô materno de y, x é avó ou avô de y, x é ascendente de y, e x é
descendente de y.

Lema 4 A composi¸cão de rela¸cões binárias é associativa.
Prova: Sejam α ⊆ A × B, β ⊆ B × C e γ ⊆ C × D rela¸cões binárias. Então,
xα(βγ)y ⇐⇒ ∃z ∈ B xαz ∧ z(βγ)y (por def. composta α(βγ))
⇐⇒ ∃z ∈ B ∃w ∈ C xαz ∧ zβw ∧ wγy (por def. composta βγ)
⇐⇒ ∃w ∈ C xαβw ∧ wγy (por def. αβ)
⇐⇒ x(αβ)γy (por def. (αβ)γ)
ou seja, ∀x ∈ A ∀y ∈ D (xα(βγ)y ⇔ x(αβ)γy). Logo, α(βγ) = (αβ)γ ou seja a composi¸cão
é associativa.
Lema 5 Seja R uma rela¸cão definida num conjunto A. Então, quaisquer que sejam os in-
teiros positivos n e k tem-se Rn+k = RnRk.
Prova: Seja R ⊆ A × A. Vamos mostrar por indu¸cão sobre n ∈ Z+ que
∀n ∈ Z+
∀k ∈ Z+ Rn+k = RnRk. (5.4)
Se n = 1 então por defini¸cão de Ri tem-se R1+k = RRk para todo k ∈ Z+, pelo que a
proposi¸cão é verdade para n = 1. Vamos mostrar agora que qualquer que seja n ∈ Z+,
( ∀k ∈ Z+
Rn+k
= Rn
Rk
=⇒ ∀k ∈ Z+
Rn+1+k
= Rn+1
Rk
).
Sejam k, n quaisquer em Z+. Tem-se,
Rn+1+k = RRn+k (por defini¸cão de Ri)
= R(RnRk) (por hipótese de indu¸cão)
= (RRn)Rk (pela associatividade da composi¸cão)
= (Rn+1)Rk (por defini¸cão de Ri)
Mostrámos que as condi¸cões do princ´ıpio de indu¸cão se verificam, pelo que se conclui por esse
princ´ıpio a validade de (5.4)
.
Proposi¸cão 25 (Caracteriza¸cão dos fechos) Seja R uma rela¸cão binária em A = ∅. O
fecho reflexivo de R é R∪IA, sendo IA a rela¸cão identidade em A (i.e., IA = {(a, a) : a ∈ A}).
O fecho simétrico de R é R ∪ R−1. O fecho transitivo de R é i∈Z+ Ri.
Prova: Qualquer rela¸cão binária em A que seja reflexiva terá que conter
{(a, a) | a ∈ A}

ou seja, IA. Por defini¸cão, o fecho reflexivo de R, seja Rref, é uma rela¸cão reflexiva, pelo que
Rref ⊇ IA. Ainda por defini¸cão, Rref ⊇ R. Assim, Rref ⊇ R ∪ IA. R ∪ IA é reflexiva, e
qualquer rela¸cão definida em A que seja reflexiva e contenha R, contém R ∪ IA. Logo, R ∪ IA
é o fecho reflexivo de R.
R ∪ R−1 contém R e é simétrica. Se (x, y) ∈ R ∪ R−1 então (x, y) ∈ R ∨ (x, y) ∈ R−1. Por
defini¸cão de inversa, se (x, y) ∈ R então (y, x) ∈ R−1, e se for (x, y) ∈ R−1 então (y, x) ∈ R.
Portanto, se (x, y) ∈ R ∪ R−1 então (y, x) ∈ R−1 ∨ (y, x) ∈ R, ou seja (y, x) ∈ R ∪ R−1, o que
prova a simetria de R ∪ R−1. Se mostrarmos que qualquer rela¸cão S definida em A que seja
simétrica e contenha R, contém R ∪ R−1, concluimos que R ∪ R−1 é o fecho simétrico de R
(por defini¸cão de fecho simétrico). Ora, se S é simétrica e S ⊇ R, então S ⊇ R−1. De facto,
(x, y) ∈ R−1 ⇒ (y, x) ∈ R (por defini¸cão de R−1)
⇒ (y, x) ∈ S (por S ⊇ R)
⇒ (x, y) ∈ S (pela simetria de S)
Logo S ⊇ R−1, e como S ⊇ R, conclui-se S ⊇ R ∪ R−1.
Resta-nos provar que o fecho transitivo de R, que denotaremos por R+, é
R+
=
i∈Z+
Ri
ou seja
R+
⊆
i∈Z+
Ri
(5.5)
R+
⊇
i∈Z+
Ri
(5.6)
Come¸camos pela primeira inclusão. Vamos provar que i∈Z+ Ri (⊆ A × A) é transitiva
e contém R, pelo que por defini¸cão de fecho transitivo se concluirá (5.5). Como R = R1
(por defini¸cão de R1), segue trivialmente R ⊆ i∈Z+ Ri. Para justificar que i∈Z+ Ri é
transitiva, sejam x, y, z ∈ A, e suponhamos que
(x, y) ∈
i∈Z+
Ri
e (y, z) ∈
i∈Z+
Ri
.
Por defini¸cão de união de rela¸cões, se (x, y) ∈ i∈Z+ Ri então existe k ∈ Z+ tal que xRky.
E analogamente, (y, z) ∈ i∈Z+ Ri ⇒ ∃p ∈ Z+ yRpz. Ou seja,
((x, y) ∈
i∈Z+
Ri
∧ (y, z) ∈
i∈Z+
Ri
) ⇒ ∃p, k ∈ Z+
xRk
y ∧ yRp
z,

o que implica ∃p, k ∈ Z+ xRkRpz. Então, pelo Lema 5, vem xRk+pz, isto é (x, z) ∈ Rk+p.
Donde, (x, z) ∈ i∈Z+ Ri. Logo, i∈Z+ Ri é transitiva.
Mostremos agora que também (5.6). Para tal, vamos usar indu¸cão sobre n ∈ Z+ para
provar que
∀n ∈ Z+
R+
⊇
1≤i≤n
Ri
o que implica a validade de (5.6). Se n = 1 então 1≤i≤n Ri = R. E, R ⊆ R+ por defini¸cão
de fecho. Supondo agora que R+ ⊇ 1≤i≤k Ri, vamos mostrar que então R+ ⊇ 1≤i≤k+1 Ri.
Sejam x, y ∈ A tais que (x, y) ∈ 1≤i≤k+1 Ri. Queremos concluir que então (x, y) ∈ R+.
Por defini¸cão de união, (x, y) ∈ 1≤i≤k+1 Ri se e só se (x, y) ∈ 1≤i≤k Ri ou (x, y) ∈ Rk+1.
Se for (x, y) ∈ 1≤i≤k Ri então, por hipótese de indu¸cão xR+y. Se for (x, y) ∈ Rk+1,
então existe z ∈ A tal que xRz ∧ zRky (uma vez que Rk+1 = RRk por defini¸cão).
Como R ⊆ R+, e Rk ⊆ 1≤i≤k Ri, e por hipótese de indu¸cão 1≤i≤k Ri ⊆ R+,
(xRz ∧ zRk
y) ⇒ (xR+
z ∧ zR+
y).
Como por defini¸cão de fecho transitivo, R+ é transitiva, vem xR+y.
Logo, pelo princ´ıpio de indu¸cão matemática é verdade que
∀n ∈ Z+
R+
⊇
1≤i≤n
Ri
De (5.5) e (5.6) segue R+ = i∈Z+ Ri.
Nota¸cão. Sendo R uma rela¸cão binária num conjunto, R+ designa o fecho transitivo de R
e R o seu fecho transitivo e reflexivo.
Exemplo 42 Seja R a rela¸cão definida em Z+ por
xRy sse y = x + 3, x, y quaisquer em Z+
R não é transitiva porque por exemplo (1, 4) ∈ R, (4, 7) ∈ R e (1, 7) /∈ R. Assim,
R ⊆ R+ = R. Vamos determinar R+, calculando i∈Z+ Ri. Cada Ri é uma rela¸cão definida
em Z+ e
R1 = R
R2 = RR = {(x, y) | ∃z ∈ Z+ xRz ∧ zRy} = {(x, y) | y = x + 6}
R3 = RR2 = {(x, y) | ∃z ∈ Z+ xRz ∧ zR2y} = {(x, y) | y = x + 9}
...
...

Para n ∈ Z+, teremos
Rn+1
= RRn
= {(x, y) | ∃z ∈ Z+
xRz ∧ zRn
y} = {(x, y) | y = x + 3(n + 1)}
o que pode ser provado por indu¸cão sobre n. Assim,
R+
=
i∈Z+
Ri
= {(x, y) ∈ Z+
× Z+
| ∃k ∈ Z+
y = x + 3k}.
O fecho simétrico e transitivo de R, seja Rst, é
Rst = {(x, y) ∈ Z+
× Z+
| ∃k ∈ Z y = x + 3k}
Pode-se mostrar que o fecho simétrico e transitivo é sempre o fecho transitivo do fecho
simétrico.
Exerc´ıcio 5.5.2 Seja R uma rela¸cão definida em A.
a) Mostre que se R é simétrica então R+ é simétrica.
b) Usando se necessário a al´ınea anterior, prove que o fecho simétrico e transitivo de R é
(R ∪ R−1)+, ou seja o fecho transitivo do fecho simétrico de R.
c) Verifique se
(a) o fecho simétrico e transitivo é o fecho simétrico do fecho transitivo.
(b) o fecho transitivo e reflexivo é o fecho transitivo do fecho reflexivo.
(c) o fecho transitivo e reflexivo é o fecho reflexivo do fecho transitivo.
5.5.2 Fecho transitivo duma rela¸cão definida num conjunto finito
Mostrámos que o fecho transitivo é dado por uma união infinita de rela¸cões. No entanto, em
certos casos essa união pode-se reduzir de facto a uma união finita.
Corolário 25.1 Seja R ⊆ A × A (com A não necessariamente finito). Se existir algum
inteiro positivo m tal que Rm+1 ⊆ 1≤k≤m Rk, então R+ = 1≤k≤m Rk.
Prova: Seja R ⊆ A × A tal que Rm+1 ⊆ 1≤k≤m Rk, para algum m ∈ Z+.
Vamos mostrar por indu¸cão sobre k que
∀k ≥ m + 1 Rk ⊆ 1≤i≤m Ri (5.7)

pelo que, R+ = i∈Z+ Ri ⊆ 1≤i≤m Ri. Como também i∈Z+ Ri ⊇ 1≤i≤m Ri, conclui-se
R+ = 1≤i≤m Ri.
A validade no caso k = m + 1 é trivial, já que Rm+1 está nas condi¸cões do corolário.
Tomemos como hipótese de indu¸cão a validade de (5.7) para um qualquer k ≥ m + 1 fixo,
e vamos mostrar que então também é válida para k + 1.
Mostrar que Rk+1 ⊆ 1≤i≤m Ri equivale a verificar que para todo x, y ∈ A,
(x, y) ∈ Rk+1
⇒ (x, y) ∈
1≤i≤m
Ri
,
Por defini¸cão de Rk+1 tem-se (x, y) ∈ Rk+1 se e só se existe z ∈ A tal que xRz ∧ zRky.
Usando a hipótese de indu¸cão sobre Rk, vem xRz e z 1≤i≤m Ri y. Logo, por defini¸cão de
união, existe p ≤ m, tal que zRpy . Assim, existe z ∈ A tal que xRz e zRpy. Donde,
xRp+1y. Como p + 1 ≤ m + 1, vem
Rp+1
⊆
1≤i≤m+1
Ri
=
1≤i≤m
Ri
.
Logo, (x, y) ∈ 1≤i≤m Ri. Portanto, por indu¸cão matemática, (5.7) é válida.
Corolário 25.2 Seja R uma rela¸cão definida em A (não necessariamente finito). Se existir
m ∈ Z+ tal que Rm = ∅ então R+ = 1≤k≤m−1 Rk (supõe-se que é vazia a união das rela¸cões
Rk com 1 ≤ k ≤ 0).
Prova: Se Rm = ∅, para algum m ∈ Z+, então ∀k ≥ m Rk = ∅. Assim, R+ = m−1
k=1 Rk.
A prova também é imediata se se recorrer ao Corolário 25.1. Já que Rm ⊆ m−1
k=1 Rk se
Rm = ∅.
Corolário 25.3 Seja R uma rela¸cão definida num conjunto finito A, e seja n = |A|. Então
Rn+1 ⊆ 1≤j≤n Rj e R+ = 1≤j≤n Rj
Prova: Sejam x, y ∈ A tais que xRn+1y. Então pelo Lema 3, existem x1, . . . xn tais que
xRx1 ∧ . . . ∧ xnRy.
Como A só tem n elementos distintos, ou ocorrem repeti¸cões em x1, . . . , xn, ou x e y
ocorrem em x1, . . . xn.
Se for xi = xj para algum (i, j) com i = j, então podemos retirar xiRxi+1 ∧ . . . ∧ xj−1Rxj
e escrever xRx1 ∧. . . ∧xi−1Rxi ∧xiRxj+1 . . . ∧xnRy identificando xi−1 com x caso seja i = 1,
e xj+1 com y se for j = n. Logo xRn+1−j+iy.

Se não existirem repeti¸cões em x1, . . . xn, então x = xi para algum i.
Podemos então escrever simplesmente xRxi+1 ∧ . . . ∧ xnRy identificando xi+1 com y caso
i = n. Donde, xRn+1−iy.
Mostrou-se que quaisquer que sejam x, y ∈ A se xRn+1y então existe k ≤ n tal que xRky.
Logo, Rn+1 ⊆ 1≤j≤n Rj.
Então, pelo Corolário 25.1, R+ = 1≤j≤n Rj.
Exemplo 43 Seja R a rela¸cão binária em {1, 2, 3, 4, 5, 6, 7} representada pelo grafo seguinte.
1• GG 2•

GG 5• GG 6•
oo

4•
yy
3•oo 7•
yy
Já determinámos anteriormente R+ por análise do grafo. Também poderiamos ter determi-
nado R+ analiticamente: R+ = R ∪ R2 ∪ R3 ∪ R4 ∪ R5 ∪ R6 ∪ R7.
MR2 = (MR)2
= MRMR
MR3 = MR2 MR
MR4 = (MR)4
= MR2 MR2
MR5 = MR4 MR
...
MR+ = MR ∨ MR2 ∨ MR3 ∨ MR4 ∨ MR5 ∨ MR6 ∨ MR7
Exerc´ıcio 5.5.3 Justifique que quaisquer que sejam R e S definidas num conjunto A finito
e não vazio, MR∪S[i, j] = MR[i, j] ∨ MS[i, j] com 1 ≤ i, j ≤ |A|.
Exemplo 44 Note que se R for a rela¸cão definida em {1, 2, 3, 4} representada pelo grafo
seguinte
1• GG 2•

4•
yy
3•oo
então (x, x) ∈ R+ para todo x ∈ {1, 2, 3, 4} mas (x, x) /∈ Ri para todo i 4. Neste caso,
R+ = R ∪ R2 ∪ R3 ∪ R4 = {1, 2, 3, 4} × {1, 2, 3, 4}.

Cap´ıtulo 6
Grafos e Multigrafos
Os grafos representam um modelo fundamental em Computa¸cão, surgindo em
• problemas de caminhos (por exemplo, caminho m´ınimo ou máximo);
• representa¸cão de redes (por exemplo, de computadores);
• descri¸cão de sequência de programas;
• desenho de circuitos integrados;
• representa¸cão de rela¸cões (por exemplo, ordena¸cão, emparelhamento);
• análise sintáctica de linguagens (árvores sintáticas), etc.
frase
{{vvvvv
BB…………………………………
fn
55rrrrrr
}}{{{{
fv
55qqqqq
zzuuuuuuu
det

n

v

fn
zzvvvvv

det

n

o rato ca¸cou o gato
6.1 Grafos Dirigidos
Um grafo dirigido é definido por um par G = (V, E) em que V é um conjunto de vértices e
E um conjunto de ramos orientados que ligam pares de vértices de V , não existindo mais do
que um ramo com a mesma orienta¸cão a ligar dois vértices.

6.1. GRAFOS DIRIGIDOS 72
Quando o conjunto de vértices é finito (o que implica que o conjunto de ramos também
o seja), o grafo é finito, podendo-se desenhar. Por exemplo,
•1

GG •2
GFEDBCoo GG •3 •5
GFEDBCoo •6
•4
yy aa||||||||
GF@ABCyy
é um grafo em que o conjunto de ramos é E = {(1, 4), (1, 2), (2, 2), (2, 3), (4, 1), (4, 4), (5, 5)} e
o conjunto de vértices é V = {1, 2, 3, 4, 5, 6}.
Se (x, y) ∈ E, então o vértice x é a origem e o vértice y o fim do ramo (x, y), dizendo-se
que x e y são os extremos do ramo (x, y) e que o ramo é incidente em y.
Os arcos da forma (x, x), isto é com origem e fim no mesmo vértice, chamam-se lacetes.
No exemplo, são três os ramos incidentes no vértice 2, isto é, que terminam no vértice 2.
Este vértice tem grau de entrada três e grau de sa´ıda dois.
O grau de entrada dum vértice é o número de ramos que têm fim nesse vértice. O grau
de sa´ıda é o número de ramos que têm origem nesse vértice.
No exemplo, os vértices 5 e 6 são vértices isolados, pois não são origem nem fim de
nenhum ramo com algum extremo noutro vértice.
Um percurso (finito) é uma sequência finita formada por um ou mais ramos do grafo
tal que o extremo final de qualquer ramo coincide com o extremo inicial do ramo seguinte
na sequência. Um percurso num grafo dirigido fica bem identificado se se indicar a sequência
de vértices por onde passa. Para o exemplo, o percurso (1, 4), (4, 1), (1, 2), (2, 2), (2, 2), (2, 3)
pode ser dado pela sequência de vértices 1, 4, 1, 2, 2, 2, 3.
A origem do percurso é a origem do primeiro ramo no percurso e o fim do percurso é
o fim do último ramo no percurso. Um percurso com origem em v e fim em w é um percurso
de v para w. Chama-se circuito a um percurso em que a origem e o fim coincidem. O
comprimento (ou ordem) dum percurso (finito) é o número de ramos que o constituem.
Assim, 1, 4, 1, 2, 2, 2, 3 tem origem em 1, fim em 3 e comprimento seis, não sendo um
circuito. Note que, qualquer percurso de comprimento k envolve k + 1 vértices, não necessa-
riamente distintos.
Neste percurso, alguns vértices são visitados mais do que uma vez, concretamente os
vértices 1 e 2, e o ramo (2, 2) é usado mais do que uma vez.
Na terminologia moderna para grafos, caminho é um percurso sem repeti¸cão de vértices
e ciclo é um percurso fechado que não tem repeti¸cão de vértices com excep¸cão do inicial e
final. Designa-se por pista um percurso que não contém repeti¸cão de ramos.

A terminologia de grafos é pouco consistente, pelo que é sempre necessário contextualizar
cada termo usado na bibliografia da área. Na terminologia clássica de grafos usava-se a
designa¸cão de caminho como sinónimo de percurso. Chamava-se então caminho simples a um
percurso em que nenhum ramo ocorre duas ou mais vezes e caminho elementar a um percurso
em que nenhum vértice ocorre duas ou mais vezes. De acordo com a mesma terminologia,
ciclo era sinónimo de circuito, chamando-se “ciclo simples” se fosse também caminho simples.
6.1.1 Multigrafos dirigidos.
O conceito de grafo pode ser de certo modo generalizado para permitir a existência de vários
ramos com a mesma origem e fim. Multigrafo dirigido é um terno (V, A, Φ) em que V é um
conjunto de vértices (ou nós), A um conjunto de ramos (ou arestas) e Φ é uma fun¸cão
de A em V × V que a cada ramo associa um par de vértices.
Assim, um grafo dirigido (simples) é um multigrafo dirigido (V, A, Φ) em Φ é uma
fun¸cão injectiva. Cada par ordenado de vértices fica associado por Φ quando muito a um
ramo. Um grafo dirigido fica bem definido por um par (V, ρ) em que ρ é uma rela¸cão binária
em V, ou seja, um conjunto de pares ordenados. Cada par é um ramo.
A origem e o fim dum ramo α tal que Φ(α) = (u, v) são os vértices u e v respecti-
vamente. Usam-se também as designa¸cões de: nó inicial (final), vértice inicial (final) e
extremos.
Num multigrafo dirigido, o grau de entrada dum vértice é o número de ramos que têm
fim nesse vértice; o grau de sa´ıda é o número de ramos que têm origem nesse vértice.
Exemplo 45 Considere o multigrafo dirigido representado na figura.
v1
α5

α6

α7

@AGFα1
ED α2
GG
v2
α3
oo
EDBC α4
@Ayy
v3
α8
bb}}}}}}}}}}}}}}}}
V = {v1, v2, v3}
A = { α1, α2, α3, α4, α5, α6, α7, α8}
Ψ = {(α1, (v1, v1)), (α2, (v1, v2)), (α3, (v2, v1)), (α4, (v2, v2)),
(α5, (v1, v3)), (α6, (v1, v3)), (α7, (v1, v3)), (α8, (v3, v2)) }

Pode-se observar que o grau de entrada de v1 é 2 e o seu grau de sa´ıda é 5.
A sequência de ramos α1α5α8α3α6 é um percurso de v1 para v3 (tem ciclos). Este percurso
não fica bem determinado se só indicar a sequência de vértices por onde passa.
Um percurso (finito) num multigrafo é uma sequência finita formada por um ou mais
ramos do multigrafo e tal que o extremo final de qualquer ramo coincide com o extremo
inicial do ramo seguinte na sequência. Representamos um percurso pelo tuplo dos seus ramos
(α1, . . . , αk) ou simplesmente α1 . . . αk.
Um percurso num grafo dirigido fica bem representado se se indicar a sequência de vértices
por onde passa. Assim, se αi = (vi, vi+1), então (v1, . . . vk, vk+1) representa um e um só
percurso num grafo dirigido. Também poderemos representar por v1 . . . vkvk+1.
A origem do percurso é a origem do primeiro ramo no percurso e o fim do percurso é
o fim do último ramo no percurso. Um percurso com origem em v e fim em w é um percurso
de v para w.
O comprimento (ou ordem) dum percurso (finito) é o número de ramos que o consti-
tuem.
Um circuito é um percurso fechado, ou seja, um percurso cuja origem e fim coincidem.
Um lacete (loop) é um circuito de ordem 1.
6.1.2 Grafos, Percursos e rela¸cões binárias
Grafo de uma rela¸cão binária R definida em A é um grafo dirigido (V, ρ): os vértices
do grafo identificam-se com os elementos do conjunto A e a rela¸cão ρ com a rela¸cão R.
Proposi¸cão 26 (cf. Lema 3, cap´ıtulo 5) Seja G = (V, ρ) um grafo dirigido e sejam u e
v vértices em V. Dado k ∈ Z+ existe percurso de u para v de comprimento k se e só se
(u, v) ∈ ρk.
Corolário 26.1 (cf. Proposi¸cão 25, cap´ıtulo 5)) Seja G = (V, ρ) um grafo dirigido. Sejam
u e v vértices em V. Existe algum percurso de u para v se e só se (u, v) ∈ ρ+, sendo ρ+ o
fecho transitivo de ρ.
Notando que qualquer percurso de comprimento k envolve k + 1 vértices facilmente se
mostra a seguinte proposi¸cão.

6.2. GRAFOS N ÃO DIRIGIDOS 75
Corolário 26.2 Seja G = (V, ρ) um grafo dirigido finito. Qualquer percurso de ordem maior
ou igual a |V| contém um circuito.
Corolário 26.3 (por Corolários 25.3, cap´ıtulo 5)) e 26.2 ) Seja G = (V, ρ) um grafo dirigido
finito. Sejam u e v vértices em V. Existe algum percurso de u para v se e só se existe algum
percurso de u para v de ordem não superior ao |V|. E, se u = v então existe algum percurso
de u para v se e só se existe algum percurso de u para v de ordem inferior ao |V|.
Paralelamente, também se pode mostrar que se R é uma rela¸cão binária num conjunto
finito A, |A| = n ≥ 2 e x, y ∈ A são distintos, então xRny se e só se existir p, tal que
1 ≤ p n e (x, y) ∈ Rp. Verifique que este resultado não pode ser generalizado a pares da
forma (x, x). Compare com o Corolário 25.3, cap´ıtulo 5.
Dados u e v vértices de um multigrafo dirigido, diz-se que v é acess´ıvel de u se e só se
u = v ou existe no multigrafo algum percurso de u para v.
Um multigrafo dirigido G é fortemente conexo se e só se qualquer vértice é acess´ıvel de
qualquer outro vértice nesse multigrafo.
Corolário 26.4 Um grafo dirigido G = (V, ρ) é fortemente conexo se e só se ρ = V × V ,
sendo ρ o fecho transitivo e reflexivo de ρ.
6.2 Grafos Não Dirigidos
Multigrafo não dirigido é um terno (V, E, Φ) em que V é um conjunto de vértices (ou
nós), E um conjunto de ramos e Φ é uma fun¸cão de E no conjunto de pares não ordenados
de elementos de V. Escreve-se Φ(α) = u, v . Usaremos u, v ou {u, v} para representar um
par não ordenado.
Grafo não dirigido (simples) é um multigrafo não dirigido (V, E, Φ) em que Φ é uma
fun¸cão injectiva. Cada par de vértices não ordenado fica associado por Φ quando muito a um
ramo.
v1
v2
ffffffff
||||||||
v3 v4
v1 v5

v2
ffffffff
||||||||
v3 v4
À esquerda está representado um multigrafo não dirigido que não é grafo dirigido, já que há
mais do que um ramo a ligar v1 e v2. À direita temos um grafo não dirigido.

Multigrafo adjunto de um multigrafo não dirigido G = (V, E, Φ) é um multigrafo diri-
gido GA = (V, A, Ψ) tal que a cada ramo de E unindo vértices diferentes correspondem dois
ramos em A, e vice-versa. Se Φ(α) = u, v e u = v então existem dois ramos α1 e α2 em A
tais que Ψ(α1) = (u, v) e Ψ(α2) = (v, u).
O grafo adjunto de um grafo não dirigido G = (V, E, Φ) é um grafo dirigido (V, ρ) em que
ρ é simétrica. Tem-se (u, v) ∈ ρ e (v, u) ∈ ρ sse Φ(α) = u, v para algum α ∈ E.
Se Φ(α) = u, v então u e v dizem-se extremos do ramo α.
Um percurso (finito) num multigrafo não dirigido é uma sequência finita formada por
um ou mais ramos do multigrafo que corresponde a um percurso no multigrafo adjunto.
Num grafo não dirigido ( v0, v1 , v1, v2 , . . . vk−1, vk ) representa um percurso entre v0 e
vk. Se se indicar a sequência de vértices por onde um percurso passa, (v0, v1, v2, . . . , vk−1, vk)
pode ser entendido como um percurso de v0 para vk.
O comprimento (ou ordem) dum percurso (finito) é o seu número de ramos.
Um circuito num grafo não dirigido é um percurso fechado ( v0, v1 , v1, v2 , . . . vk−1, vk )
que v0 e vk coincidem. Um ciclo (por vezes designado ciclo simples) é um circuito que não
tem repeti¸cão de vértices com excep¸cão do inicial e final.
Um grafo não dirigido é ac´ıclico se e só se não contém ciclos (nem lacetes).
v1
v2
ffffffff
||||||||
v3 v4
v1 v5

v2
ffffffff
||||||||
v3 v4
tem circuitos tem ciclos (simples)
não tem ciclos (simples) não é ac´ıclico
Grau de um vértice num grafo não dirigido é o número de ramos que têm esse vértice
como extremo.
Um subgrafo1 de um grafo G = (V, E) é um grafo G = (V , E ) em que V ⊆ V, E ⊆ E.
Também se pode definir subgrafo de um multigrafo (dirigido ou não).
1
Alguns autores consideram ainda que E terá que ter todos os ramos de E que unem vértices em V ,
chamando subgrafo parcial se algum ramo que liga vértices em V não pertencer a E .

6.2.1 Grafos Conexos
Num multigrafo não dirigido, dado um par de vértices u, v diz-se que v é acess´ıvel de u se
e só se u = v ou existe no multigrafo algum percurso entre u e v. Facilmente se reconhece
que a rela¸cão “acessibilidade” é de equivalência.
Um multigrafo não dirigido G é conexo se e só se qualquer vértice é acess´ıvel de qualquer
outro vértice nesse multigrafo.
Dado um qualquer multigrafo não dirigido G, pode-se mostrar que cada classe de equi-
valência da rela¸cão de acessibilidade corresponde a um subgrafo de G que é conexo e que
é máximo (no sentido deixa de ser conexo se se tentar juntar mais algum vértice de G).
Tais subgrafos dizem-se componentes conexas de G. Por abuso de linguagem, chamare-
mos ainda componentes conexas às classes de equivalência da rela¸cão de acessibilidade. O
conjunto de vértices na componente identifica-a perfeitamente.
O multigrafo (não dirigido) seguinte tem duas componentes conexas.
v1
v2
vvvvvv
vvvvvv
rrrrrr
v3 v4
v5 v6
iiiiiiiiiiiiii
v7
vvvvvv
v8
A rela¸cão de acessibilidade não depende da existência de vários ramos entre dois vértices.
A cada multigrafo não dirigido podemos associar um grafo não dirigido substituindo cada
conjunto de ramos entre um mesmo par de vértices por apenas um ramo. Podemos ainda
retirar todos os lacetes. O grafo não dirigido assim definido determina a mesma rela¸cão de
acessibilidade que o multigrafo dado.
Proposi¸cão 27 Um multigrafo não dirigido é conexo se e só se o seu multigrafo adjunto é
fortemente conexo.
Lema 6 Seja G = (V, ρ) um grafo não dirigido finito, conexo, |ρ| ≥ 1.
(i) Se se retirar um ramo de G, o grafo resultante tem quando muito duas componentes
conexas.
(ii) Seja v um vértice de G. Se v tem grau m, então se retirar v e todos os ramos com
extremo em v, o grafo resultante tem quando muito m componentes conexas.

Exerc´ıcio 6.2.1 Prove o Lema 6. Para (i), suponha que o ramo u, v é retirado. Considere
Av assim definido
Av = {w ∈ V | w = v ou existe percurso em G entre w e v que não inclui o ramo u, v }
e mostre que se VAv = ∅ então u /∈ Av e VAv é o conjunto
{w ∈ V | w = u ou existe algum percurso em G entre w e u que não inclui o ramo u, v }
e Av e VAv correspondem a subgrafos conexos (e maximais) de G, ou seja componentes
conexas. Para (ii), use indu¸cão sobre o número de ramos retirados.
6.2.2 Condi¸cão necessária para um grafo ser conexo
Pretende-se ligar um conjunto de localidades, seja {l1, l2, . . . , ln}, por estradas. Qual o número
m´ınimo de estradas a construir para que seja poss´ıvel chegar de qualquer localidade a qualquer
uma das restantes?
O resultado enunciado a seguir, permite dar uma primeira resposta a tal questão – “pelo
menos n−1 estradas terão que ser constru´ıdas”. Esse número é suficiente desde que as liga¸cões
sejam feitas com algum cuidado (cf. Proposi¸cão 29 à frente).
Proposi¸cão 28 É condi¸cão necessária para que um qualquer grafo não dirigido e finito (V, E)
seja conexo que |E| ≥ |V| − 1.
Prova: Vamos mostrar por indu¸cão sobre o número de vértices do grafo que
∀n ∈ Z+
∀G G = (V, E) grafo não dirigido conexo, |V| = n ⇒ |E| ≥ |V| − 1
A condi¸cão é verdadeira para n = 1 já que o grafo não dirigido com 1 só vértice e zero
ramos é trivialmente conexo. Vamos tomar como hipótese de indu¸cão a validade da condi¸cão
para todos os grafos não dirigidos e conexos cujo número de vértices não excede k. Ou seja,
∀1 ≤ i ≤ k ∈ Z+
∀G G = (V, E) grafo não dirigido conexo, |V| = i ⇒ |E| ≥ |V| − 1
e vamos mostrar que então a proposi¸cão é válida para grafos com k + 1 vértices.
Seja G um grafo não dirigido conexo e com k + 1 vértices. Como G não tem vértices
isolados (já que G é conexo e k + 1 ≥ 2) seja v um qualquer vértice de V e seja p ≥ 1 o
seu grau. Considere-se o subgrafo que se obtém retirando v e os p ramos com extremo em v.
Pelo Lema 6, tal grafo é constitu´ıdo por m (m ≤ p) componentes conexas: sejam G1, . . . Gm.
Cada um dos Gi é não dirigido, conexo, e tem um número de vértices (seja ni) não superior

6.3. ÁRVORES 79
a k. Então, por hipótese de indu¸cão, o número de ramos de cada Gi é maior ou igual a ni −1.
Donde,
|E| ≥ p +
m
i=1
(ni − 1) = p + k − m ≥ k = |V| − 1
Note que cada vértice pertence a uma só componente conexa, pelo que m
i=1 ni = k.
Conclui-se assim por indu¸cão matemática que se G = (V, E) é não dirigido, finito e conexo,
então |E| ≥ |V| − 1.
Exerc´ıcio 6.2.2 Mostre que o rec´ıproco da Proposi¸cão 28 é falso ou seja, que existem grafos
não dirigidos que não são conexos embora |E| ≥ |V| − 1.
Lema 7 Seja G um grafo não dirigido conexo. Se G não é ac´ıclico então é poss´ıvel retirar
algum ramo a G de modo que o grafo resultante seja também conexo.
Lema 8 Seja G um grafo não dirigido conexo e com pelo menos 2 vértices, tal que se se
retirar algum ramo, o grafo resultante é não conexo. Então G tem pelo menos dois vértices
de grau 1.
Exerc´ıcio 6.2.3 Prove os Lemas 7 e 8. Para mostrar 8 use indu¸cão sobre o número de
vértices do grafo, e se necessário o resultado (i) do Lema 6.
6.3 Árvores
Árvore é um grafo não dirigido conexo com n vértices e n − 1 ramos. Se tiver 1 vértice (e 0
ramos) diz-se árvore degenerada.
•
•
tttttt
tttttt
• •
tttttt
tttttt •
• •
• •
iiiiiiiiiiiii
•
tttttt
•
•
tttttt •
• •
tttttt
•
tttttt
tttttt • •
• •
árvore não é árvore árvore
Proposi¸cão 29 (caracteriza¸cão das árvores) São equivalentes as seguintes caracteriza¸cões
de árvores não degeneradas. Árvore não degenerada é um grafo não dirigido com n 1
vértices
1. conexo e ac´ıclico.

6.3. ÁRVORES 80
2. tal que entre cada par de vértices (distintos) existe um só caminho.
3. conexo, e se se retirar algum ramo ( u, v , u = v) o grafo deixa de ser conexo.
4. conexo e se se juntar mais algum ramo sem alterar o conjunto de vértices, o grafo fica
com um e um só ciclo (simples).
5. ac´ıclico e com n − 1 ramos.
6. conexo e com n − 1 ramos.
Prova: Vamos provar a equivalência das caracteriza¸cões mostrando
(1) ⇒ (2) ⇒ (3) ⇒ (4) ⇒ (1)
(1) ⇒ (5) ⇒ (6) ⇒ (1).
• (1) ⇒ (2) já que se C e C fossem dois caminhos distintos entre u e v, para algum par
de vértices u, v de G, então CC seria um circuito em G (e conteria um ciclo) pelo que
G não seria ac´ıclico.
• (2) ⇒ (3) já que se se retirar um ramo, seja u, v , o grafo deixa de ser conexo, pois
passa a não existir caminho entre u e v, uma vez que entre cada par de vértices de G
existia um e um só caminho.
• (3) ⇒ (4) se se juntar mais um ramo, seja u, v = α então como já existia caminho em
G entre u e v forma-se um ciclo, Cα (em que C era o caminho entre u e v). Se se formar
um outro ciclo, então α tem também que estar nesse ciclo. Seja αC , esse outro ciclo.
Então C é um caminho entre u e v diferente de C, pelo que CC é um ciclo em G. É
poss´ıvel retirar um ramo em CC sem que o grafo passe a ser não conexo (cf. Lema 7),
o que contraria (3).
• (4) ⇒ (1) se G já tivesse algum ciclo então se se juntar um ramo entre dois vértices no
ciclo, forma-se pelo menos dois ciclos, o que contraria (4). Logo, G é ac´ıclico.
Concluimos assim que (1), (2), (3), e (4) são equivalentes. Para completar a prova da
Proposi¸cão, vamos mostrar agora a equivalência de (1), (5) e (6).
• (1) ⇒ (5) (por indu¸cão sobre o número de vértices) Se o grafo tiver exactamente 2
vértices então tem apenas um ramo, e se for um vértice isolado, então tem 0 ramos
(senão não seria ac´ıclico). Tomamos como hipótese de indu¸cão a validade da condi¸cão
para grafos com i vértices, 1 ≤ i ≤ k. E, vamos mostrar que então ainda é válida para
grafos com k + 1 vértices.

6.3. ÁRVORES 81
Seja G = (V, E) um grafo com k + 1 vértices, conexo e ac´ıclico. Como G é conexo e
tem pelo menos dois vértices, então tem ramos. Retire-se um ramo de G, seja u, v .
Como já mostrámos que (1) e (3) são equivalentes, o grafo resultante é não conexo. Pelo
Lema 6 podemos afirmar que tem exactamente duas componentes conexas: sejam G1 e
G2. Sejam n1 e n2 o número de vértices respectivos. Então 1 ≤ ni ≤ k, e como cada
Gi é um subgrafo ac´ıclico (senão G conteria ciclos) e conexo, terá que ter ni − 1 ramos
(por hipótese de indu¸cão). Consequentemente,
|E| = (n1 − 1) + (n2 − 1) + 1 = (n1 + n2) − 1 = (k + 1) − 1 = k = |V| − 1.
Portanto, por indu¸cão matemática podemos concluir que qualquer grafo não dirigido
finito, ac´ıclico e conexo tem exactamente menos um ramo do que vértices.
• (5) ⇒ (6) Seja G um grafo qualquer com k vértices ac´ıclico e com k−1 ramos. Se G não
for conexo, então seja m o número de componentes conexas de G. Como G é ac´ıclico,
cada componente conexa é ac´ıclica pelo que tem exactamente ni − 1 ramos, se for ni
o seu número de vértices. Isto porque, já mostrámos que (1) ⇒ (5), e se alguma das
componentes se reduzir a um vértice terá que ter zero ramos.
Então k − 1 = m
i=1(ni − 1) = k − m. Logo, m = 1, ou seja, G só tem uma componente
conexa, sendo portanto conexo.
• (6) ⇒ (1) Se o grafo não fosse ac´ıclico então, pelo Lema 7, poderiamos retirar um ramo,
sendo o grafo resultante ainda conexo. Como o grafo dado tinha n − 1 ramos, então o
novo grafo teria n−2 ramos e seria conexo, o que contraria o resultado da Proposi¸cão 28.
Logo, se G é conexo com n − 1 ramos então G é conexo e ac´ıclico. 2
Numa árvore não degenerada, os vértices com grau 1 chamam-se folhas e os de grau
superior chamam-se nós internos ou simplesmente nós.
6.3.1 Árvores com ra´ız
Árvore com ra´ız é um grafo dirigido com n vértices e n − 1 ramos e tal que existe um e um
só vértice do qual todos são acess´ıveis. Tal vértice chama-se a ra´ız da árvore. As folhas numa
árvore com ra´ız são os vértices com grau de sa´ıda zero. A ra´ız da árvore é o único vértice
com grau de entrada zero. Numa árvore com ra´ız os filhos ou descendentes directos de
um nó v são os extremos finais de ramos com origem em v. Os descendentes de um nó são
os filhos desse nó e os descendentes dos filhos desse nó. Um nó é pai dos seus filhos.

6.4. PERCURSOS EULERIANOS E HAMILTONIANOS 82
Árvore ordenada (ou orientada ) é uma árvore com ra´ız e tal que o conjunto de ramos
que saem dum vértice está totalmente ordenado.
As árvores sintácticas são árvores ordenadas.
frase
}}zzzz
AAƒƒƒƒƒƒƒƒƒƒƒ
fn
33hhhhh
ÐÐÑÑÑÑ
fv
33gggg
||yyyyyy
det

n

v

fn
}}zzzz

det

n

o rato ca¸cou o gato
expr
yysssss

BB……………………………
expr

expr
yysssss

77uuuuu
inteiro

expr

expr

inteiro

inteiro

5 + 3 + 8
As árvores seguintes poderiam iguais se se considerasse que eram árvores com ra´ız, mas
são diferentes se se considerar que são árvores ordenadas (e 1 2).
•
1
~~~~~~~
2
11ddddddd
•
1
~~~~~~~
2
11ddddddd •
• •
•
1
~~~~~~~
2
11ddddddd
• •
1
~~~~~~~
2
11ddddddd
• •
Os valores atribu´ıdos aos ramos especificam a ordem subentendida. Em geral, não se colocam
esses valores pois convenciona-se que a representa¸cão já obedece a essa ordem: ou o ramo mais
à esquerda é o maior ou é o menor. Uma árvore ordenada diz-se árvore n-ária se o grau
de sa´ıda de cada vértice não excede n. As árvores das figura anterior são árvores binárias.
Quando se tem uma árvore binária é usual falar da sub-árvore direita e na sub-árvore
esquerda dum nó.
6.4 Percursos Eulerianos e Hamiltonianos
Um percurso de Euler num multigrafo é uma pista (ie, percurso sem repeti¸cão de ramos)
que inclui todos os ramos desse multigrafo. Se tal percurso é um circuito diz-se circuito de
Euler.
Um exemplo clássico de aplica¸cão é o Problema das sete pontes de Königsberg ([Euler,
1736]): pretende-se partir dum local da cidade e regressar ao mesmo local passando por cada
ponte exactamente uma vez.
eeee eeee
¡¡¡¡¡¡¡¡

6.5. GRAFOS PLANARES 83
Proposi¸cão 30 Seja G um grafo não dirigido, finito e sem vértices isolados. Existe um
circuito de Euler em G se e só se G é conexo e todos os vértices de G têm grau par. Existe
um percurso de Euler em G se e só se G é conexo e o número de vértices em G com grau
´ımpar é 0 ou 2.
Exerc´ıcio 6.4.1 Verifique se é poss´ıvel desenhar cada uma das figuras sem levantar o lápis
do papel e sem desenhar duas vezes a mesma linha, baseando-se na Proposi¸cão 30.
Um percurso de Hamilton (1859) num multigrafo é um percurso que passa por cada
vértice do multigrafo uma e uma só vez.
Um circuito de Hamilton é um circuito com origem e fim no mesmo vértice e que passa
por cada um dos restantes vértices do multigrafo uma e uma só vez. Serve de modelo ao
Problema do caixeiro viajante, que tendo que visitar várias localidades, pretende saber qual
o melhor caminho a percorrer sem passar (se poss´ıvel) duas vezes na mesma localidade.
Não se conhece qualquer condi¸cão necessária e suficiente que garanta a existência dum
percurso (nem dum circuito) de Hamilton num grafo. Apenas para alguns casos particulares.
Por exemplo: existe percurso hamiltoniano em qualquer grafo não dirigido completo com pelo
menos dois vértices.
Um grafo não dirigido, finito e sem lacetes, e tal que existe um ramo entre cada par de
vértices diferentes, diz-se completo. O grafo completo com n vértices, denota-se por Kn.
6.5 Grafos Planares
Um grafo é planar sse for poss´ıvel representá-lo no plano sem que haja cruzamento de ramos.
Exerc´ıcio 6.5.1 Justifique que o grafo (V, E) é planar, para V = {1, 2, 3, 4, 5, 6, 7, 8} e E =
{ 1, 2 , 1, 8 , 1, 6 , 2, 3 , 2, 7 , 3, 8 , 3, 4 , 4, 5 , 4, 7 , 5, 6 , 5, 8 , 6, 7 }.
Um grafo não dirigido (V, E) diz-se bipartido se e só se existir uma parti¸cão {V1, V2} do
conjunto V tal que para todo v1, v2 ∈ E se tem v1 ∈ V1 e v2 ∈ V2.

6.6. ISOMORFISMO DE GRAFOS 84
Se cada vértice em V1 estiver ligado a cada um dos vértices de V2 por um ramo, o grafo
diz-se bipartido completo. Nesse caso, se |V1| = m e |V2| = n, o grafo denota-se por Km,n.
Na figura apresenta-se K3,3 (bipartido completo) e K5 (completo, não bipartido).
•
ddddddd
GGGGGGGGGGGGGG •
•
~~~~~~~
ddddddd •
•
~~~~~~~

•
•
~~~~~~~
ddddddd

GGGGGGGGGGGGGG
•
yyyyyyyyyyyyyy •
oooooooooooooo
• •
Estes dois grafos não são planares.
O Teorema de Kuratowski (1930) afirma que um grafo não dirigido finito não é planar
se e só se tiver como subgrafo K5 ou K3,3 ou algum grafo que possa ser obtido de K5 ou K3,3
por inser¸cão ou elimina¸cão de vértices de grau 2. A prova deste teorema está fora do âmbito
da disciplina.
6.6 Isomorfismo de Grafos
Dois grafos dirigidos (V1, E1) e (V2, E2) são isomorfos se e só se existir uma bijeçcão f de V1
em V2 tal que (v1, v2) ∈ E1 sse (f(v1), f(v2)) ∈ E2. De modo semelhante, diz-se que dois
grafos não dirigidos (V1, E1) e (V2, E2) são isomorfos se e só se existir uma bijeçcão f de V1
em V2 tal que v1, v2 ∈ E1 sse f(v1), f(v2) ∈ E2. Tais bijeçcões preservam a estrutura de
liga¸cões do grafo.
Por exemplo, os dois grafos seguintes são isomorfos, o que nos permite concluir que o grafo
desenhado à esquerda é planar.
a b
c d
1 2
3 4
A seguir apresentam-se (a menos de isomorfismo) todos os grafos não dirigidos conexos
que têm n vértices, para 1 ≤ n ≤ 4.

6.7. COLORAÇ ÃO DE GRAFOS 85
1
2
3
4
6.7 Colora¸cão de Grafos
Considere o mapa da Europa. Qual é o número m´ınimo de cores necessário para colorir o
mapa de forma que pa´ıses que têm fronteira comum sejam coloridos com cores diferentes? O
problema tem por modelo o seguinte problema de grafos.
Seja G = (V, E) não dirigido finito. O número cromático é o menor número de cores
necessárias para colorir os vértices do grafo de forma que se u = v e u, v ∈ E, então u e v
ficam com cores distintas.
Exerc´ıcio 6.7.1 Qual o número cromático de cada um dos grafos seguintes?
Qual é o número cromático duma árvore não degenerada? E dum grafo bipartido? E de Kn?
O Teorema das 4 cores diz que o número cromático de qualquer grafo não dirigido finito
que seja planar não excede quatro. Este teorema foi durante mais de 100 anos uma conjectura
(ie, resultado cuja validade não foi demonstrada nem a falsidade). Enunciado por F. Guthrie
em 1850, só foi provado em 1976 por K. Appel e W. Haken, com ajuda dum computador para
efectuar a análise dalguns casos relevantes. A sua prova está fora do âmbito da disciplina.
Exerc´ıcio 6.7.2 Uma loja de animais de estima¸cão, recebeu uma encomenda de peixes tro-
picais. Algumas das espécies comem outras espécies. Sabendo que o grafo (não conexo)

6.8. GRAFOS COM VALORES ASSOCIADOS AOS RAMOS 86
apresentado no exerc´ıcio anterior representa as incompatibilidades das diferentes espécies,
justifique que o número m´ınimo de aquários necessários é igual ao número cromático do
mesmo. Justifique que é sempre assim, qualquer que seja a rela¸cão de incompatibilidade.
6.8 Grafos com Valores Associados aos Ramos
Um multigrafo com valores associadas aos ramos é um quarteto (V, E, Φ, L) em que
(V, E, Φ) é um multigrafo, e L : E −→ R+
0 é uma fun¸cão de E no conjunto dos reais não
negativos. Só iremos considerar reais não negativos.
Para um grafo dirigido podemos reduzir o quarteto a um terno (V, ρ, L). Se o grafo for
finito, então podemos associar uma matriz de distâncias D do modo seguinte:
Dij = L(vi, vj) sse (vi, vj) ∈ ρ
Dij = ∞ sse (vi, vj) /∈ ρ
para 1 ≤ i ≤ |V|, 1 ≤ j ≤ |V|. Os elementos da matriz D são elementos de R+
0 ∪ {∞}.
No exemplo seguinte, o valor que marca cada ramo representa a distância associada a esse
ramo.
a
1
ÐÐÐÐÐÐÐÐ
5
11bbbbbbbb
b
10
ÑÑÒÒÒÒÒÒÒÒ
2 GG
2
00```````` e
2
00aaaaaaaa
c d3
oo
7
ddÒÒÒÒÒÒÒÒ
1
GG f
A matriz D das distâncias associadas aos arcos é











0 1 ∞ ∞ 5 ∞
∞ 0 10 2 2 ∞
∞ ∞ 0 ∞ ∞ ∞
∞ ∞ 3 0 7 1
∞ ∞ ∞ ∞ 0 2
∞ ∞ ∞ ∞ ∞ 0











para v1 = a, v2 = b, . . . , v6 = f, tendo-se seguido a conven¸cão de que a distância de um vértice
a si próprio é zero.
Se não existir ramo de u para v convencionamos que a distância associada ao “ramo”de
u para v é ∞. Leia-se ∞ como indeterminado ou indefinido.
Os problemas de cálculo de distância m´ınima entre localidades e custo m´ınimo de produ¸cão
de um dado produto têm muitas vezes por modelo um grafo como o descrito.

A distância associada a um percurso de u para v é a soma das distâncias associadas
aos ramos no percurso. Podemos definir uma opera¸cão binária2 ⊕ em R+
0 ∪ {∞} que
prolongue a opera¸cão usual de adi¸cão em R+
0 assim:
x ⊕ y = x + y sse x ∈ R+
0 e y ∈ R+
0
x ⊕ y = ∞ sse x = ∞ ou y = ∞
Se não existir percurso de u para v, a distância de u para v é ∞.
6.8.1 Determina¸cão da distância m´ınima
Dados dois vértices u e v num grafo finito (V, ρ, L) como determinar a distância m´ınima de
u para v? Seja Cuv o conjunto dos percursos de u para v, u = v. Se Cuv = ∅ convencionamos
que a distância m´ınima para aceder de u a v é ∞. Se Cuv = ∅ então a distância m´ınima é
min{dγ | dγ é a distância pelo percurso γ, para γ ∈ Cuv.}
Como o grafo é finito, tal m´ınimo é
min{dγ | dγ é a distância por γ ∈ Cuv e a ordem de γ não excede |V| − 1}
pois os percursos com ordem (comprimento) maior que |V|−1 contêm circuitos, correspondendo-
lhes por isso distâncias iguais ou superiores.
Dado um grafo finito (V, ρ, L), convencionámos que a distância m´ınima entre vértices
iguais era zero. Em cada caso prático deve-se verificar se esta conven¸cão faz sentido.
Algoritmo de Bellman-Ford
Vamos designar por Dm a matriz das distâncias m´ınimas por percursos de ordem não
superior a m. Se tivermos calculado Dm, podemos obter as distâncias m´ınimas por percursos
de ordem não superior a m+1, analisando a distância associada a percursos que têm mais um
ramo do que os percursos m´ınimos obtidos anteriormente. Se esses percursos com mais um
ramo não forem melhores então deve-se dar preferência aos anteriores. Assim, Dm+1 pode
ser obtida à custa de Dm e de D1 = D, por (6.1)
Dm+1
ij = min( Dm
ij , min{ Dm
ik ⊕ Dkj | 1 ≤ k ≤ |V|} ) (6.1)
para 1 ≤ i ≤ |V|, 1 ≤ j ≤ |V|, e min definido por:
min(x, y) = x sse x ∈ R+
0 , y ∈ R+
0 , e x ≤ y
min(x, y) = y sse x ∈ R+
0 , y ∈ R+
0 , e y ≤ x
min(x, ∞) = x
min(∞, y) = y
2
Opera¸cão binária num conjunto A é uma fun¸cão de A × A em A.

A matriz das distâncias m´ınimas é uma matriz Dm tal que Dm+1 = Dm, isto é que
se mantem invariante quando se efectuar a transforma¸cão descrita.
Observa¸cão: A transforma¸cão corresponde ao cálculo da matriz Dm + Dm × D em que +
é uma “soma” de matrizes e × é um “produto” de matrizes, para matrizes quadradas cujas
entradas são elementos da estrutura (R+
0 ∪ {∞}, min, ⊕). Esta observa¸cão deve ficar clara
na disciplina de Elementos de Álgebra Linear. Compare ainda com a matriz da composta de
rela¸cões binárias.
Convencionando Dii = 0, para 1 ≤ i ≤ |V|, podemos simplificar a fórmula (6.1):
Dm+1
ij = min{Dm
ik ⊕ Dkj | 1 ≤ k ≤ |V|}
Para o exemplo anterior, as três primeiras linhas da matriz D2 são



0 1 11 3 3 7
∞ 0 5 2 2 3
∞ ∞ 0 ∞ ∞ ∞



no exemplo acima indicado. A determina¸cão das restantes linhas e o cálculo da matriz das
distâncias m´ınimas (absolutas) ficam ao cuidado do leitor. Deverá obter:











0 1 6 3 3 4
∞ 0 5 2 2 3
∞ ∞ 0 ∞ ∞ ∞
∞ ∞ 3 0 7 1
∞ ∞ ∞ ∞ 0 2
∞ ∞ ∞ ∞ ∞ 0











Algoritmo de Floyd
Supõe-se que os vértices em V foram numerados de 1 a n = |V|. O algoritmo de Floyd (1962),
apresentado na figura 6.1, permite determinar a distância e um percurso m´ınimo para todos
os pares de vértices.
O processo de constru¸cão da matriz das distâncias m´ınimas é iterativo: na itera¸cão k
obtém-se a matriz Dk das distâncias m´ınimas por percursos que só podem ter como vértices
intermédios v1, . . . , vk. (NB: Esta matriz Dk não é a mesma que se definiu acima!) Agora,
para 1 ≤ k n,
Dk+1
ij = min(Dk
ij, Dk
i k+1 + Dk
k+1 j)

Dados: a matriz D das distâncias e número de vértices n
Resultado: a matriz das distâncias m´ınimas em D e a matriz P
Inicializar P.
Para k ← 1 até n
Para i ← 1 até n
Para j ← 1 até n
Se D[i, j] D[i, k] + D[k, j] então
D[i, j] ← D[i, k] + D[k, j];
P[i, j] ← P[i, k];
Figura 6.1: Algoritmo de Floyd
já que qualquer percurso óptimo de vi para vj que só possa ter v1, . . . , vk, vk+1 como vértices
intermédios é ou um percurso óptimo que só pode ter v1, . . . , vk como vértices intermédios ou
a concatena¸cão (jun¸cão) dum percurso óptimo de vi a vk+1 com um percurso óptimo de vk+1
a vj, ambos só podendo ter v1, . . . , vk como vértices intermédios.
Note que esta descri¸cão do algoritmo não corresponde exactamente ao algoritmo apre-
sentado na figura 6.1, pois não foi considerada uma matriz de distâncias para cada itera¸cão.
Para permitir também determinar o percurso m´ınimo, o algoritmo apresentado vai
construindo uma matriz P k: a posi¸cão P k
ij guarda sempre o segundo vértice no melhor percurso
de vi para vj que se encontrou até à itera¸cão k. Inicialmente, pode-se definir,
Pij =
j se i = j ou (vi, vj) ∈ E
0 se i = j e (vi, vj) /∈ E
Poder-se-ia ter definido a matriz P doutras formas. Por exemplo, podemos tomar P k
ij
como o vértice intermédio no percurso (m´ınimo) de i para j que foi usado para determinar o
melhor valor de Dk
ij. Assim, considerando que os vértices estão numerados de 1 a n, podemos
inicialmente fazer Pij ← 0 para todo i e todo j (significando que não é conhecido nenhum
vértice intermédio no percurso de i para j). Na actualiza¸cão, quando D[i, j] D[i, k]+D[k, j],
far-se-ia Pij ← k, já que o percurso melhor de i para j encontrado até à itera¸cão k passa por k.
No final, se Dij ∞, sendo i = j, então o percurso m´ınimo de i para j é a sequência formada
por i, os vértices intermédios nesse percurso e finalmente j. Para determinar os vértices
intermédios no percurso de i para j, verifica-se Pij = 0, e se for o caso, então imprimem-se
os vértices intermédios no percurso de i para Pij, imprime-se Pij e finalmente imprimem-se
os vértices intermédios no percurso de Pij para j.

Algoritmo de Dijkstra
O algoritmo de Dijkstra (1959), apresentado na figura 6.2, calcula a distância m´ınima dum
dado vértice a todos os outros.
Dados: Um grafo G = (V, E, d) dirigido com valores nos arcos, e u0 ∈ V.
Resultado: O vector Dest das distâncias m´ınimas de v a cada um dos vértices.
Inicializar M ← {u0}, Dest[u0] ← 0 e Dest[v] ← ∞ para todo v ∈ V {u0}.
Enquanto M = V fazer
seja w o último vértice colocado em M;
actualizar a estimativa das distâncias a u0: para cada v ∈ V M fazer
Dest[v] ← min(Dest[v], Dest[w] + d(w, v)).
seja v ∈ V M tal que Dest[v] é m´ınimo;
M ← M ∪ {v}.
Figura 6.2: Algoritmo de Dijkstra
• Em cada passo, os vértices em M são aqueles para os quais já é conhecida a distância
m´ınima a partir de u0. O valor de Dest[v] para v ∈ M a distância m´ınima de u0 a v.
• Se substituir a condi¸cão M = V por uf /∈ M (sendo dado uf ∈ V), o algoritmo termina
quando a distância m´ınima de u0 a uf for conhecida. Todos os vértices que podem
ocorrer no percurso m´ınimo de u0 para uf estão em M.
• Dado uf ∈ V {u0}, o percurso m´ınimo de u0 para uf pode ser obtido por análise para
trás do modo seguinte: escolher v ∈ M com (v, uf ) ∈ E e Dest[v]+d(v, uf ) = Dest[uf ];
se v = u0, escolher v ∈ M tal que (v , v) ∈ E e Dest[v ] + d(v, v ) = Dest[v]. . . e assim
sucessivamente até chegar a u0. O percurso de u0 para uf é dado pela sequência de
vértices seleccionados, na ordem inversa da de seleçcão: a última escolha é o 1o
¯ vértice
no percurso, a penúltima o 2o
¯, . . .
• Note que a instru¸cão Dest[v] ← min(Dest[v], Dest[w] + d(w, v)) actualiza Dest[v] se
Dest[v] Dest[w]+d(w, v), tendo sido assim identificado um percurso mais curto de u0
para v, sendo w o penúltimo vértice nesse percurso. Se registar esse facto, por exemplo
num vector Prec, fazendo Prec[v] ← w, então, no final, na análise para trás, basta
imprimir
uf , Prec[uf ], Prec[Prec[uf ]], . . . , u0

para ter os vértices no (ou num) percurso min´ımo de u0 para uf (por ordem inversa).
Ou seja, escreve_percurso(v) pode ser assim definida (de forma recursiva):
Se v = u0 então escreve_percurso(Prec[v])
Escreve v
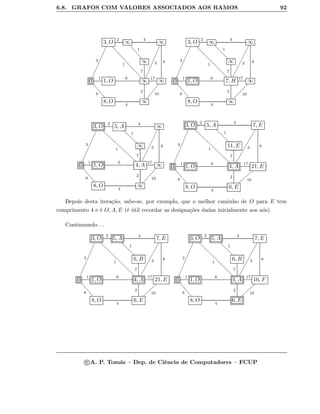
Exemplo 46 É necessário enviar uma encomenda para um cliente em C, a qual pode ser
enviada via A, H ou G, demorando três, um e oito dias, respectivamente a chegar a esses
locais. O quadro seguinte indica os pares de locais entre os quais há transporte directo e ainda
o tempo (em dias) que demora no m´ınimo o transporte entre esses locais. Se a encomenda for
enviada hoje e encaminhada com máxima prioridade (por pagamento duma taxa adicional),
quando é que se espera que o cliente a receba?
A e B 2 B e D 4 B e G 1 A e E 1 H e E 6 E e G 7
G e F 4 E e D 3 C e E 17 F e C 10 F e E 2 C e D 8
Representamos a rede de transportes esquematicamente: O designa a origem.
A
2
1
WWWWWWWWWWWWWWWW B
4
1
WWWWWWW D
8G
7
O
3
1
8 WWWWWWW H
6
E
17
3

C
G 4
F
2
10
ÕÕÕÕÕÕÕ
∞ 2
1
aaaaaaaaaaaaaaaaa ∞ 4
1
aaaaaaa ∞
8∞
7
0
3
1
8 XXXXXXX ∞ 6
∞ 17
3

∞
∞
4
∞
2
10
ÒÒÒÒÒÒÒ
Para não complicar o grafo, representámo-lo como um grafo não dirigido, devendo ser claro
que d(u, v) = d(v, u). Aplicamos o algoritmo de Dijkstra para determinar a distância m´ınima
da origem a cada um dos locais: acima, à direita, indicamos os valores iniciais de D. À
medida que formos efectuando actualiza¸cões, registamos o vértice que as determinou, para no
fim poder, por análise para trás, recuperar o caminho m´ınimo.

3, O
2
1
aaaaaaaaaaaaaaaaa
∞ 4
1
YYYYYYYY ∞
8∞
7
0
3
1
8 XXXXXXX 1, O
6
∞ 17
3

∞
8, O
4
∞
2
10
ÕÕÕÕÕÕÕÕ
3, O
2
1
ccccccccccccccccc
∞ 4
1
cccccccc ∞
8∞
7
0
3
1
8 XXXXXXX 1, O
6
7, H
17
3

∞
8, O
4
∞
2
10
ÑÑÑÑÑÑÑÑ
3, O
2
1
eeeeeeeeeeeeeeeeee
5, A
4
1
eeeeeeee
∞
8∞
7
0
3
1
8 XXXXXXX 1, O
6
4, A
17
3

∞
8, O 4
∞
2
10
ÒÒÒÒÒÒÒÒ
3, O
2
1
eeeeeeeeeeeeeeeeeee
5, A
4
1
ffffffff
7, E
811, E
7
0
3
1
8 XXXXXXX 1, O
6
4, A
17
3

21, E
8, O
4
6, E
2
10
zzzzzzzz
Depois desta itera¸cão, sabe-se, por exemplo, que o melhor caminho de O para E tem
comprimento 4 e é O, A, E (é útil recordar as designa¸cões dadas inicialmente aos nós).
Continuando. . .
3, O
2
1
ddddddddddddddddddd
5, A
4
1
ddddddd
7, E
86, B
7
0
3
1
8 XXXXXXX 1, O
6
4, A
17
3

21, E
8, O 4
6, E
2
10
||||||||
3, O
2
1
ddddddddddddddddddd
5, A
4
1
ddddddd
7, E
86, B
7
0
3
1
8 XXXXXXX 1, O
6
4, A
17
3

16, F
8, O 4
6, E
2
10
||||||||

6.9. GRAFOS COM SÍMBOLOS ASSOCIADOS AOS RAMOS 93
3, O
2
1
ddddddddddddddddddd
5, A
4
1
ddddddd
7, E
86, B
7
0
3
1
8 XXXXXXX 1, O
6
4, A
17
3

16, F
8, O 4
6, E
2
10
||||||||
3, O
2
1
ddddddddddddddddddd
5, A
4
1
ddddddd
7, E
86, B
7
0
3
1
8 XXXXXXX 1, O
6
4, A
17
3

15, D
8, O 4
6, E
2
10
||||||||
3, O
2
1
ddddddddddddddddddd
5, A
4
1
ddddddd
7, E
86, B
7
0
3
1
8 XXXXXXX 1, O
6
4, A
17
3

15, D
8, O
4
6, E
2
10
||||||||
3, O
2
11ddddddddddddddddddd
1
ddddddddddddddddddd
5, A
4
1
ddddddd
7, E

86, B
7
0
3

rr 1
8 XXXXXXX 1, O
6
4, A
17
pp
3

15, D
8, O
4
6, E
2
10
||||||||
A encomenda chega daqui por 15 dias, devendo ser enviada via A, depois de A para E,
de E para D e de D para C.
NB: Na resolu¸cão do problema à mão, pode efectuar as altera¸cões num só grafo: para
poder conferir os passos, é conveniente não apagar as marca¸cões anteriores (quando as altera),
devendo antes riscá-las (parcialmente) de forma a continuarem vis´ıveis.
6.9 Grafos com S´ımbolos Associados aos Ramos
Um multigrafo com s´ımbolos associados aos ramos é um quinteto
(V, E, Σ, Ψ, L)
em que (V, E, Ψ) é um multigrafo, Σ é um conjunto (de s´ımbolos), e L é uma fun¸cão de E
em Σ que a cada ramo associa um elemento de Σ. A cada percurso num multigrafo dessa
forma corresponde uma sequência de s´ımbolos.

6.9. GRAFOS COM SÍMBOLOS ASSOCIADOS AOS RAMOS 94
Considere-se por exemplo o grafo representado a seguir.
m0GFED@ABCBCEDb
GF
a GG m1GFED@ABCBCEDcGF
O conjunto Σ de s´ımbolos é {a, b, c}. As sequências em
{b, bb, bbb, bbbb, bbbbb, bbbbbb, . . .}
correspondem a percursos de m0 para m0. Assim esses percursos determinam as sequências
de s´ımbolos de Σ que só têm b’s. As sequências em
{c, cc, ccc, cccc, ccccc, . . .}
correspondem a percursos de m1 para m1. As sequências em
{a, ba, bba, bbba, . . . , ac, bac, bbac, bbbac, . . . , acc, bacc, bbacc, bbbacc . . .}
correspondem a percursos de m0 para m1. Podemos dizer que estes percursos determinam as
sequências de s´ımbolos de Σ que têm um e um só a podendo ter b’s antes e c’s depois do a.
Exemplo 47 Para o grafo seguinte, sendo d´ıgito qualquer caracter em {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
e ponto o caracter “.”, conclui-se que as sequências que correspondem a percursos de “procura
dig´ıto” para “procura ponto” são sequências de d´ıgitos e as que terminam em “procura não
d´ıgito” são da forma “x.y” ou “x.”, em que x e y são duas sequências de d´ıgitos quaisquer.
procura d´ıgito
d´ıgito
GG procura ponto
BCED d´ıgitoGF
ponto
GG procura não d´ıgito
BCED d´ıgitoGF
Se este diagrama traduzir estados num algoritmo de reconhecimento de sequências das
formas “x”, “x.” e “x.y”, em que x e y são duas sequências de d´ıgitos quaisquer, cada um
dos nós identifica um estado. Os ramos definem transi¸cões de estado. Para ver que assim é,
analise a sequência 56.099971, partindo de “procura d´ıgito” (estado inicial).
Estes grafos são de facto modelos formais de computa¸cão e serão estudados em profundi-
dade na disciplina de Modelos de Computa¸cão.

Bibliografia
[1] T. H. Cormen, C. E. Leiserson, R. L. Rivest, Introduction to Algorithms. MIT Press,
11a
¯Ed., 1994.
[2] R. P. Grimaldi. Discrete and combinatorial mathematics : an applied introduction. 4a
¯Ed.,
Addison Wesley, 1999.
[3] C. L. Liu. Elements of Discrete Mathematics, McGraw-Hill, 1977.
[4] F. P. Preparata, and R. T. Yeh. Introduction to discrete structures, Addison-Wesley,
1973.
[5] A. P. Tomás. Notas de Tópicos de Matemática Discreta, DCC, FCUP, 1997.
[6] A. P. Tomás. Modelos de Computa¸cão – Acetatos das aulas teóricas, DCC, FCUP, 1998.
[7] A. P. Tomás, N. Moreira. Introdu¸cão aos Computadores – Notas e Exerc´ıcios, DCC,
FCUP, 1996.

Apontamentos

Mais conteúdo relacionado

Mais procurados

Semelhante a Apontamentos

Mais de Francisco Augusto de Junito

Apontamentos