Este teste de matemática contém 12 questões sobre geometria espacial e plana, incluindo representações de figuras geométricas em sistemas de coordenadas cartesianas tridimensionais e bidimensionais. As questões abordam tópicos como perímetros, planos, esferas, triângulos, prisma e simetria.

1. Cole aqui a
fotocópia
reduzida
da sua
proposta
ESCOLA SECUNDÁRIA IBN MUCANA
Ano Lectivo 2006/2007
Matemática A – 10º Ano
2º Teste Sumativo A
17 Novembro 06
Aluno: nº: ____ Turma: ___
1ª Parte
Para cada uma das questões desta primeira parte, selecciona a resposta correcta entre as alternativas que te são
apresentadas. Se apresentares mais do que uma resposta, a questão será anulada, o mesmo sucedendo se a letra for ilegível.
1. O perímetro de um quadrado cuja diagonal mede 6 cm é:
(A)
2
6
(B) 220 (C) 23 (D) 212
2. A recta que contém os pontos A(1 , 3) e B(1 , 5) passa também no ponto de coordenadas:
(A) (5 , 1) (B) (2 , 3) (C) (1 , 6) (D) (9 , 0)
3. Na figura junta, o conjunto sombreado pode ser definido pela condição:
(A) 13 −≤∧≤ yx
(B) 13 −≤∨≤ yx
(C) 31 ≤∧−≤ yx
(D) 31 ≤∨−≤ yx
4. O ponto B ( -1,2, 3) é o simétrico de A (1,2, 3) em relação:
(A) à recta x = 2 ∧ y = 3 (B) ao eixo Ox (C) ao plano x =1· (D) ao plano yOz
5. Qual das seguintes afirmações é falsa?
(A) O plano de equação 7−=z é paralelo ao eixo 0x .
(B) O plano de equação 7−=z não contém a origem do referencial.
(C) O plano de equação 7−=z contém o ponto )7,30,2( −− .
(D) O plano de equação 7−=z é paralelo ao plano y0z .
Pg 1 de 3

2. 6 Se os planos α e β definidos num referencial ortogonal e monométrico Oxyz por z = 3 e z = -1, respectivamente,
e se a esfera é tangente a ambos, então uma condição que define a esfera
nesse referencial pode ser:
(A) 2222
≤++ zyx
(B) 2)1()1( 222
≤−+++ zyx
(C) 4)1()1( 222
≤−+++ zyx
(D) 4)1()1()1( 222
≤+++++ zyx
2ª Parte
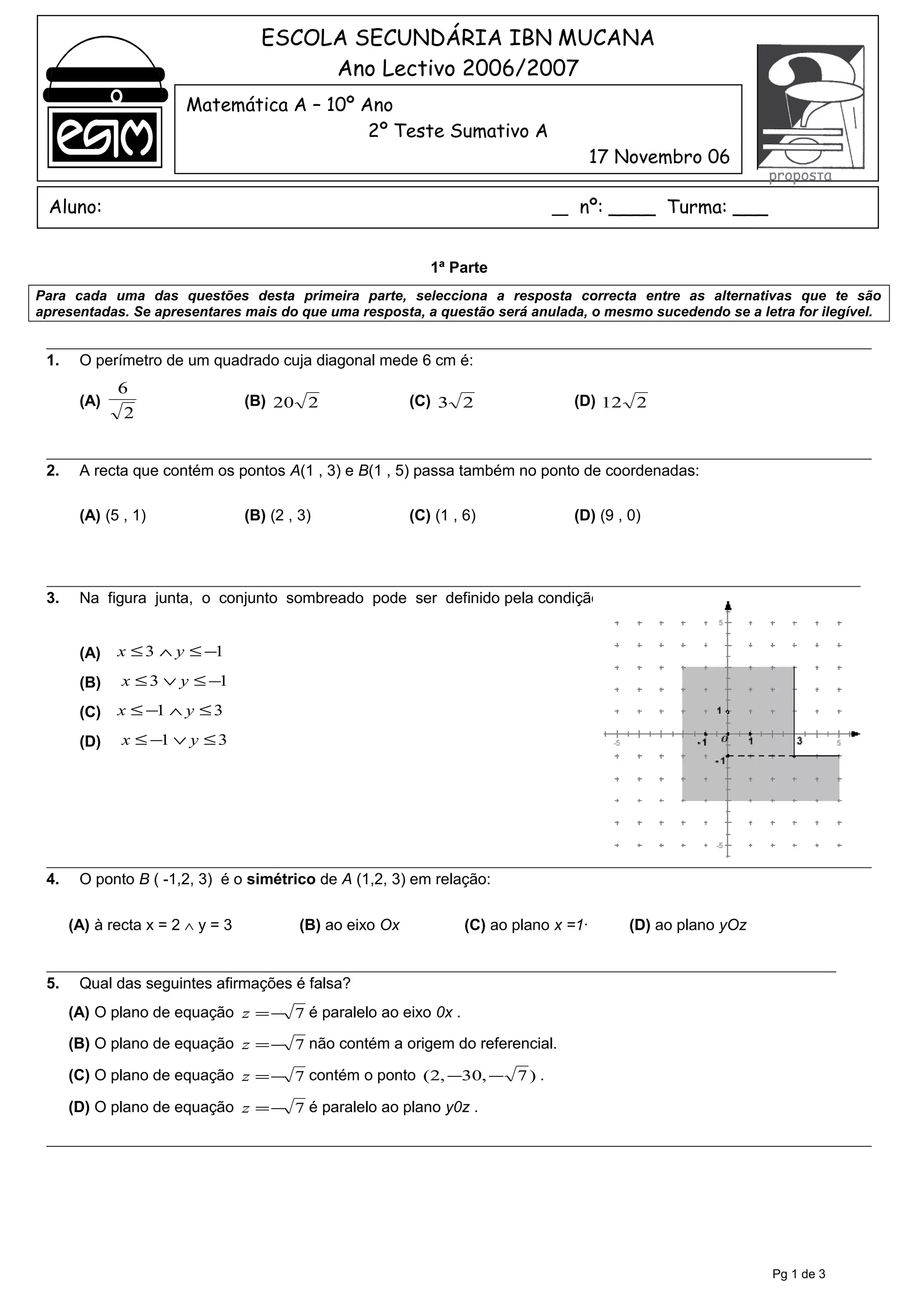
7. Na figura [ABC] é um triângulo rectângulo e o quadrilátero a sombreado é um quadrado.
Se os catetos do triângulo medem 15 cm e 10 cm, quanto mede o lado do quadrado?
8. As condições 1−≥x e 52 ≤≤ y representam diferentes regiões do plano.
8.1 Indica as coordenadas de 4 pontos:
- um ponto G que verifique apenas a primeira condição,
- um ponto H que verifique apenas a segunda,
- um ponto I que verifique as duas
- um ponto J que não verifique nenhuma delas.
8.2 Representa num referencial a região do plano definida pela condição 1−≥x ∧ 52 ≤≤ y .
9. Desenha no seu papel um referencial ortogonal e monométrico, considerando cada unidade com dois
quadradinhos do papel (ou 1 cm).
9.1. Representa no referencial os pontos A = ( 2,1 ), B = ( 3,6 ) e C = (.3,0 )
9.2. Classifica o triângulo [ABC] quanto aos lados e verifique se é rectângulo. Justifique a sua resposta.
10. Escreve as condições que representam os conjuntos de pontos das figuras seguintes:
10.1.
10.2.
Pg 2 de 3
x
y

3. 11. Representa num referencial cartesiano ortogonal e monométrico a região plana definida pela condição:
~ [ 216)4( 22
>∨>−+ yyx ]
12. Na figura está representado, em referencial Oxyz, um prisma recto quadrangular regular, de dimensões 4 x 4 x 6 cm
em que os vértices C e D se encontram no eixo dos yy.
12.1. Indica as coordenadas de todos os vértices do prisma
12.2. Identifica com letras da figura, os lugares geométricos
caracterizados pelas seguintes condições:
12.2.1) y = - 4 ∧ z = 4
12.2.2) z = 4 ∧ - 4 ≤ y ≤2 ∧ 4 ≤ x ≤0
12.3) Escreve uma condição que represente cada um dos
seguintes conjuntos de pontos:
12.3.1) aresta [BC]
12.3.2) plano AEF
12.4) Indica as coordenadas dos pontos simétricos de:
12.4.1) E relativamente ao eixo coordenado Oy.
12.4.2) A relativamente ao plano coordenado yOz
12.5. Desenha a secção produzida no prisma pelo plano HGI.
FIM
Questão Cotação Questão Cotação Questão Cotação
1. 9 8.2. 10 12.2.2. 8
2. 9 9.1. 3 12.3.1. 7
3. 9 9.2. 12 12.3.2. 4
4. 9 10.1. 12 12.4.1. 5
5. 9 10.2. 15 12.4.2. 5
6. 9 11. 14 12.5. 10
7. 15 12.1. 8
8.1. 12 12.2.1. 6
Pg 3 de 3
I