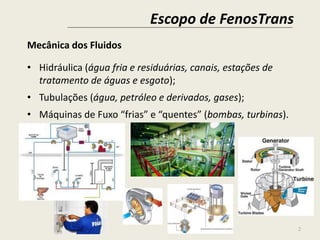
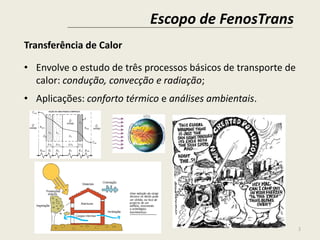
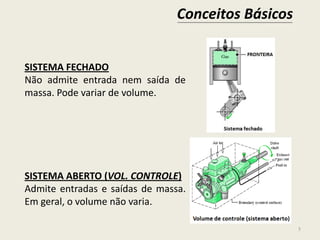
Este documento apresenta conceitos básicos de mecânica dos fluidos e fenômenos de transporte. Aborda tópicos como escopo da disciplina, sistemas fechados e abertos, propriedades extensivas e intensivas, unidades do SI, massa específica, pressão, viscosidade e tipos de fluidos newtonianos e não-newtonianos. Inclui também exemplos de problemas e equações conceituais.

1. 
Elementos Básicos Introdutórios
Fenômenos de Transporte
Prof. Ricardo Cruz

2. Escopo de FenosTrans
2
Mecânica dos Fluidos
• Hidráulica (água fria e residuárias, canais, estações de
tratamento de águas e esgoto);
• Tubulações (água, petróleo e derivados, gases);
• Máquinas de Fuxo “frias” e “quentes” (bombas, turbinas).

3. Escopo de FenosTrans
3
Transferência de Calor
• Envolve o estudo de três processos básicos de transporte de
calor: condução, convecção e radiação;
• Aplicações: conforto térmico e análises ambientais.

4. 4
MECÂNICA DOS FLUIDOS
Bibliografia
YOUNG, Donald F., MUNON, Bruce R., OKIISHI,
Theodore H. Uma Introdução Concisa à Mecânica
dos Fluidos. 2ª. Ed. Editora Edgard Blücher, SP,
2001.
ROMA, Woodrow N. L. Fenômenos de Transporte
para Engenharia. Ed. Rima. SP, 2003.

5. Conceitos Básicos
5
SISTEMA FECHADO
Não admite entrada nem saída de
massa. Pode variar de volume.
SISTEMA ABERTO (VOL. CONTROLE)
Admite entradas e saídas de massa.
Em geral, o volume não varia.

6. Conceitos Básicos
6
PROPRIEDADE EXTENSIVA (PE)
- Toda PE depende da massa da substância;
- Valores de uma PE podem ser somados, ou seja, a soma de
dois valores de uma PE leva a um terceiro valor.
Ex.: V = 1 litro de água + 3 litro de óleo = 4 litro de água suja
m = 2 kg de água + 5 kg de sal = 7 kg de salmoura
PROPRIEDADE INTENSIVA (PI)
- Toda PI independe da massa da sua substância;
- Valores de uma PE não podem ser somados.
Ex.: T = 50 C de água + 30 C de água ≠ 80 C de água

7. Unidades Adotadas
7
SISTEMA INTERNACIONAL DE UNIDADES (SI)
- Foi instituido no Brasil em 1967, derivado do sistema métrico
(SM), aqui chegado no início do séc. XIX;
- O SM é obra do Iluminismo, consequência da Revolução
Francesa, em contraposição ao confuso sistema inglês;
- As unidades mais importantes do SI são:
Massa (m): quilograma, kg
Comprimento (L): metro, m
Força (F): newton, [N]  [kg]∙9,81 [m/s²] *
Tempo (t): segundo, s
Temperatura (T): kelvin, K
Energia (E): joule, [J]  [N]∙[m]
* g = 9,81 m/s² é a aceleração da gravidade padrão.

8. Unidades Adotadas
8
UNIDADES USADAS NESTE CURSO
- Aqui só usaremos o bom SI;
- Usaremos, além das unidades mostradas no slide anterior:
Pressão (p): pascal, [Pa]  [N] / [m²]
quilopascal, kPa  1 000 Pa
megapascal , Mpa  1 000 000 Pa
bar  100 kPa  100 000 Pa
atm  1,013∙bar  101,3 kPa
Temperatura (T): celcius, [C]  [K]  273,15 (bastam 273)

9. E pra não dizer que não falei de flores…
9
SISTEMAS INGLÊS (SING) E ESTADUNIDENSE (SESTA)
- São uma “salada” de padrões. A milha e o pé vem dos romanos.
Outras… (veja http://guiadoscuriosos.com.br/blog/2012/06/26/
entenda-as-peculiares-unidades-de-medida-inglesas/);
- As unidades mais importantes do SING e do SESTA são:
Massa (m): libra-massa, lbm  0,454∙kg (SING)
slug  lbm / 32,17 (SESTA)
Comprimento (L): pé, ft  0,304 8∙m (SING/SESTA)
Força (F): lb-força, lbf  4,448 2∙N (SING/SESTA)
SING: [lbf]  1 [lbm]∙32,17 [ft/s²] / 32,17 ; SESTA: [lbf]  1 [slug]∙1 [ft/s²]
Tempo (t): segundo, s (SING/SESTA)
Temperatura (T): rankine, R  0,555 6∙K (SING/SESTA)
Energia (E): British thermal unit, Btu  1 055,056∙J (SING)
libra-força-pé, lbf.ft  778,2∙Btu (SESTA)

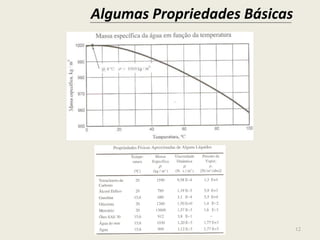
10. Algumas Propriedades Básicas
10
MASSA ESPECÍFICA
- A massa específica, ou massa por unidade de volume, de
fluido é definida como:
  lim (m/V) , [kg/m³]
V → V0
- Esta definição diz que  só tem sen-
tido para volumes além de um limite (V0), abaixo do qual a
matéria não é homogênea (hipótese do continuum);
- Massa específica é uma propriedade do SI. É mais
apropriada para líquidos;
- Um conceito associado é o volume específico: v = 1/
[m³/kg]. É mais apropriado para gases.

11. Algumas Propriedades Básicas
11
PESO ESPECÍFICO
- Não é uma propriedade reconhecida pelo SI. Deriva da
massa específica:
 =  g , [N/m³]
onde g = 9,81 m/s² é a aceleração da gravidade padrão.
- Tanto  como  dependem da temperatura: se T aumenta,
estas duas diminuem, e vice-versa;
- A água é diferente: a 4 C, seu  é máximo (próximo slide).

12. Algumas Propriedades Básicas
12

13. Algumas Propriedades Básicas
13
DENSIDADE
- Também não é uma propriedade reconhecida pelo SI.
Deriva da massa específica;
- Se define como a relação entre a massa específica da
substância e a massa específica da água a 4 C, e por isso é
adimensional:
d  subst. / ág.4C
- Sua grande aplicação é na área de derivados do petróleo.
Os institutos internacionais que regulam essa atividade
utilizam suas próprias definições de densidade. Uma das
mais antigas são os graus API.

14. Probleminhas Básicos
14
1
Vapor flui pelos dispositivos da figura abaixo: a válvula (V)
regula a vazão, a turbina (TV) produz potência e esta
movimenta o gerador elétrico (G).
A) Para a V e a TV como sistema: identifique os pontos na
fronteira onde o sistema interage com as vizinhanças;
B) Repita isso, com tudo dentro do sistema.
(V)
(TV)
(G)

15. 15
2
A figura abaixo representa uma planta térmica de potência.
A) Caracterize as entidades físicas com as quais cada
dispositivo interage com suas vizinhanças imediatas;
B) Repita o item anterior para toda a planta. O que se torna
dispensável?
C) Essas entidades são PE ou PI?

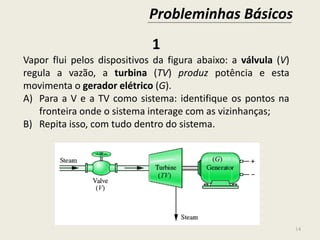
16. 16
3
Na lista seguinte de variáveis físicas (entidades), quais são PE,
PI ou nenhuma delas? : p [bar], F [N], V [m³], v [m³/kg], 
[kg/m³], T [K], a [m/s²], m [kg], L [m], t [s] e V [m/s].
4
Uma maneira simples de medir a aceleração da gravidade (AG)
de um local é usando uma mola linear (F=k x), como no caso
seguinte: em um local onde já se sabia que a AG vale g = 9,81
m/s², mede-se a distenção de uma mola em 0,739 m. Aí, no
local cuja AG se quer medir se lê que a mesma mola distende
0,742 m (por ex., em uma grande jazida de minério de ferro).
Qual o valor da AG nesse local? (resp.: 9,85 m/s²)

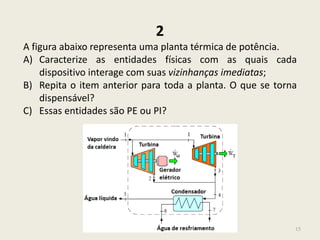
17. 17
5
Um sistema fechado consiste de 15 kg de água líquida que
ocupa certo volume. Determine esse volume, o peso do
sistema e seu peso específica, num local onde g = 9,78 m/s² e
 = 1000 kg/m³.
6
A figura ao lado ilustra um cilindro de
sucata prensada, suspensa num local onde
g = 9,82 m/s². Alguém modelou a variação
da massa específica deste cilindro como:
suc. = 7 800 – 360(z/L)² , [kg/m³]
Determine a leitura do peso no medidor, em
[N], para as medidas indicadas na figura.

18. 18
PRESSÃO
- Conceito físico que se define pela mesma lógica da massa
específica. No caso, é uma relação entre a força normal que
moléculas de um fluido exercem sobre uma superfície, assim:
p  lim (Fn /A) , [N/m²]
A → A0
- A “mesma lógica”, no caso, é que p só tem sentido acima de
certa área limite (A0), pois abaixo dela a distribuição das
moléculas não é uniforme (hipótese do continuum).
Algumas Propriedades Básicas
(continuação)
Fn
A

19. Algumas Propriedades Básicas
19
PRESSÕES RELATIVA, VÁCUO E ABSOLUTA
- São conceitos relacionados à física real dos sistemas, do
ponto de vista de como se podem efetuar os cálculos com
pressões. Isso fica mais evidente pelo diagrama abaixo;
- Seja: pamb. = 1 atm a pressão atmosférica ambiente.*
p1rel. = p1abs. – pamb.
(também chamada de
pressão manométrica)
p2vác. = p2abs. – pamb.
(notar: p2vác. < 0)
* Mais precisamente, 1 atm  101,3 kPa

20. Algumas Propriedades Básicas
20
DISPOSITIVOS PARA MEDIÇÃO DE PRESSÃO
Manômetro diferencial:
Rege-se pela relação
p = patm + lm g L
Onde lm é a massa específica do líqui-
do manométrico (mercúrio ou água).
Célula piezoelétrica: transdu-
ção do sinal elétrico para re-
gistro em um PC.
Tubo Bourdon (1849): usa o formato ovalado de um
tubo de parede fina para acionar um ponteiro.
MD usado em medições precisas.
L

21. Probleminhas Básicos
21
7
Ar a temperatura e pressão normais contidos num tanque adere
bem à hipótese do continuum. Porém, quando suficiente ar for
evacuado do tanque leva a que a hipótese não se aplique mais ao
ar restante. Por que?
8
Certa planilha de testes registra uma pressão de admissão de
uma bomba rotodinâmica igual a –10 kPa. O que esta pressão
negativa quer dizer?
9
Um sistema fechado manauara consiste de ar em repouso a
1 atm e 33 C. Do ponto de vista macroscópico, o sistema está
parado. Mas do ponto de vista microscópico, as moléculas estão
em movimento variado. Reconcilie esta aparente contradição.

22. 22
10
Frequentemente se ignora a variação da pressão com a
altitude para um gás contido em um cilindro isolado. Por que?
11
Abrir uma porta externa de teatros dotados de grandes
exaustores é barra, devido à diferença de pressões entre o ar
interior e o ar exterior. Você acha que conseguiria abrir uma
porta de 7’7’ em Manaus, onde a pressão atmosférica é 30
pol.Hg, se a pressão interna for 406,9 pol.H2O?

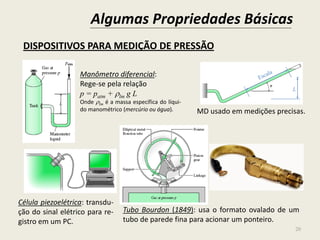
23. 23
12
A pressão absoluta dentro de um tanque é 0,4 bar e a
atmosférica local é 98 kPa. Qual seria a leitura de um
manômetro Bourdon instalado nesse tanque, em [kPa]? Essa
leitura é pressão manométrica ou vácuo?
13
Explique o porquê da “tal” precisão do manômetro de tubo
inclinado da figura abaixo.

24. VISCOSIDADE ABSOLUTA ()
Foi definida por Isaac Newton, no séc. XVII, por um experimento en-
genhoso: em uma canaleta com água, ele puxou um flutuador usan-
do uma corda, que arrastava a água debaixo dele;
Tendo que no fundo U = 0, Newton assumiu que a velocidade cresce
deste valor ao valor da placa tracionada, de forma linear, como se
ilustra abaixo.
Ele obteve que a tensão de cisalhamento das camadas de água é:
Onde:  [N.s/m²]  [Pa.s]  [kg/m.s] é o
coeficiente de viscosidade dinâmica do
fluido considerado.













dy
dU
A
F
dy
dU
A
F
p
tg
p
tg

Algumas Propriedades Básicas
(continuação)
24

25. Algumas Propriedades Básicas
25
A derivada dU/dy (taxa de deformação por cisalhamento) significa
matematicamente o gradiente de velocidade na direção y;
Como a equação de  é uma reta
que sai da origem,  significa o
coeficiente angular dessa reta
(figura ao lado).
No fluido ideal,  = 0.
 varia com a temperatura.
Se T aumenta:
- Nos líquidos:  diminui;
- Nos gases:  aumenta;
Cada fluido tem valores de  diferen-
tes com a T (slide 27).

26. Algumas Propriedades Básicas
26
A Reologia: ramo da MecFlu que estuda deformações em líquidos;
Os fluidos são newtonianos ou não newtonianos (figura abaixo):
- Plásticos de Bingham (plásticos ideais): só se deformam após certo valor
0 da tensão cisalhante. São assim pastas de dentes e graxas em geral. São
modelados como . Nesta equação, se 0 = 0 o comporta-
mento é newtoniano;
- Fluidos cuja viscosidade não é constante: obedecem ao seguinte modelo
generalizado
onde:
é a vis-
cosidade aparente, newton. é
a viscosidade newtoniana e
n é um expoente de escala.
< 1 – Tixotrópicos ou tixoplásticos: apar.  com a deformação (suspensões coloidais, tintas e polpa de papel);
> 1 – Dilatantes: apar.  com a deformação (areia movediça);
= 1 – Newtonianos.
 dydu  0
 dyduapar. 
  1
..


n
newtonapar dydu
n

27. Algumas Propriedades Básicas
27
Os derivados de petróleo geralmente tem suas viscosidades dinâmicas
dadas em centipoise, [cP]  [kg/m.s]/1000 (figura abaixo). É uma
unidade simples: a 20 C (293 K),  ág.  1 cP.

28. Algumas Propriedades Básicas
28
,

29. Algumas Propriedades Básicas
29
MEDIÇÕES DE VISCOSIDADE
• Viscosímetro relativo de tubo capilar: na figura abaixo,
mede-se o tempo que o líquido desejado leva para escoar
entre as marcas A e B (tdes.), e compara-se com o tempo que
um líquido de referência (tref.), cuja viscosidade cinemática
é conhecida (na T do ensaio), e então, prova-se:
.
.
.
.
..
..
.
.
ref
des
ref
des
refref
desdes
ref
des
t
t
t
t







ou
BULBO: serve para
cancelar os efeitos da
capilaridade no tubo;
CUBETA: serve para
evitar gotas quando o
líquido está acabando;
TANQUE M: deve ser
largo o bastante para
que sua variação de
nível seja desprezível.
CUBETA
BULBOtdes.

30. • Viscosímetro absoluto cinemático: seu nome decorre deste
aparelho proporcionar o melhor método para determinar a
viscosidade cinemática do líquido. Na figura abaixo, o líqui-
do, cuja des. é desejada conhecer, escoa
entre os pontos B1 (de altura h1) e B2
(de altura h2) num tempo t, marcado
num cronômetro. Seja V o volume que
escoa entre B1 e B2 (lido no cone). Então:
Onde: r [m] é o raio do tubo capilar cujo comprimento
vale L [m].
Algumas Propriedades Básicas
30
 
 21
21
4
.
ln8 hhL
hh



V
trg
des


CONE
V
Δt

31. Algumas Propriedades Básicas
31
• Viscosímetro cilindros coaxiais: consiste de dois cilindros
coaxiais. Nos vazios entre eles vai o líquido. Um dos dois gira
com e o outro não. Mede-se o torque no eixo, T , necessário
para vencer o torque viscoso do líquido. Esse torque tem
relação com a viscosidade do líquido, assim:
𝜇 =
𝑇
4𝜋𝑛𝐵
𝑅 𝑒
2 − 𝑅𝑖
2
𝑅 𝑒
2
∙ 𝑅𝑖
2
Onde: 𝑇 [N.m], 𝑛 [rps], 𝐵 [m],
𝑅 𝑒 [m] e 𝑅𝑖 [m]. A vis-
cosidade é 𝜇 [kg/m.s].

32. Algumas Propriedades Básicas
32
• Viscosímetro de esfera que cai: consiste de deixar cair uma
esfera metálica num meio líquido cuja viscosidade se deseja
conhecer. O líquido impõe uma resistência à queda, dada pela
força de Stokes, e a esfera adquire velocidade cons-tante. Na
figura, o tempo de queda, medido com um cronô-metro, tem
relação direta com a viscosidade do líquido. Dis-so, a
viscosidade pode ser determinada por:
Onde: resf. [m] é o raio da esfera; esf. [kg/m³]
e líq. [kg/m³] são as massas específicas da
esfera e do líquido; e wterm.[m/s] é a
velocidade terminal da esfera.
 





 

.
..
2
.
.
9
2
term
líqesfesf
des
w
rg 


33. 33
14
Uma placa plana com 100 cm² de área, e que pesa 100 N,
desloca-se para baixo numa rampa com 45° de inclinação sobre
um filme de óleo de 0,1 cm de espessura, cuja viscosidade é
desconhecida. Sabendo-se que a placa se desloca com uma
velocidade constante de 75 cm/s, determine essa viscosidade.
15
Um viscosímetro de cilindros coaxiais é usado para medir a
viscosidade de certo líquido. Sabe-se: o cilindro interno, cujo
D = 5 cm, gira a 2 000 rpm; o cilindro externo acusa num tor-
químetro de mola o torque de 200 000 dina.cm; a folga entre
os dois cilindros vale 0,02 cm; e o líquido enche essa folga até a
altura de 4 cm. Determine a viscosidade do líquido.